Yes, you need to used the "advanced" check box, or:
https://www.metabunk.org/curve/?d=6&h=1000&r=6371&u=m&a=a&fd=60&fp=3264
These numbers are notoriously tricky, as you need to be very clear about exactly what you are calculating and ensure you're using the same underlying terminology and constants. For a detailed discussion of some of the issues, see:
https://www.metabunk.org/threads/are-lynchs-horizon-calculations-correct.7877/
Generally, you are concerned with how things look in photos, so really calculating it in pixels (or % of the height of the image) is the most practical end result.
In an interview Neil deGrasse Tyson said about Felix Baumgartner's 39 km jump: "At that height you don't see the curvature of the earth. That stuff is flat!" (Watch the video from 38:20 on)
Source: https://www.youtube.com/watch?v=0FMGTVCIDbU&t=2300s
In the context of the interview, it's obvious what Tyson was trying to say. Of course the flat-earthers took his phrase "That stuff is flat!" literally repeating it gleefully. (Read also the conversation here:
https://www.metabunk.org/threads/debunked-neil-degrasse-tyson-that-stuff-is-flat.10723/. Mick West commented there: But on the face of it his [Tyson] assertion that "you don't see the curvature of the earth" from 128,000 feet is just flat wrong.)
Should Tyson said: "At that height you don't see the curvature because it is so small." Or being more specific: "If the field of view is 60 degrees, the left-right drop angle is only xxx degrees." But how large is this angle xxx?
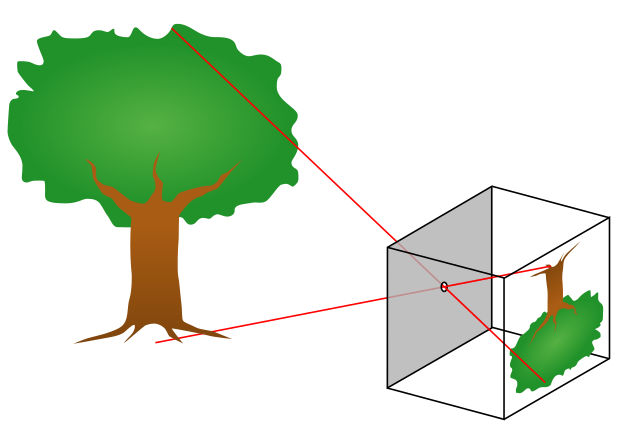
When you look at the horizon and your field of view is, let us say, 60 degrees, you see a circular segment ⌓. The height of this segment is called sagitta (or bulge). So we can ask, at which angle you see this sagitta (or what is the sagitta's angular size)?
This question has bothered me a long time. So I was happy to find the answer by Walter Bislin:
http://walter.bislins.ch/bloge/index.asp?page=Calculating+left-right+Horizon+Drop. It's purely a geometric problem to find the angle δ when R, h and α are known. Below is Bislin's general solution put together as one formula (1).
Here you get the angle δ in radians. Transform it to degrees by multiplying by 180/π.
The inequality in the "under the condition that"-expression means, that the field of view must not be too large. Otherwise the sides of the viewing angle will not touch the ball at all. The sketches below try to clarify this idea in the case where h = R. Note that the views are still in 3D. So the field of view angle α might look a little bizarre. Here δ is the angle at which the sagitta s is seen from point A. The values of δ are calculated with the formula (1).
So this is the answer I've been looking for. Now I can say in the case of Felix Baumgartner's 39 km jump:
If your field of view is 60 degrees, the left-right drop angle δ is only 0.98323 degrees. So the curvature of the horizon is really hard to see without proper measurements.
But is this the right answer after all?
Walter Bislin's calculator gives HorLftRgtDrop∠ = 0.65462°. It's about 2/3 of the value of δ which is 0.98323°. The difference is remarkable. Certainly there is a reason for this difference, but Bislin doesn't tell what it is.
Metabunk calculator gives corresponding information: "Horizon Curve refers to how much the left and right ends of the horizon are vertically lower than the middle of the image, measured in various ways. Horizon Curve Angle = Horizon Curve height expresses as a visual angle. There are two ways of calculating this which are very similar for most heights."
In the case of Felix Baumgartner's 39 km jump these values are:
– Horizon Curve Angle v1= 0.96842
– Horizon Curve Angle v2 = 0.98215
Especially v2 is at small heights almost the same as δ. In bigger heights it differs more though.
So neither calculator gives the value δ = 0.98323. Maybe the values that calculators give are more useful in analysing photographs. I really know nothing of that topic. Maybe Mick could clarify this topic a little bit? And could this pure geometric value δ be added in the calculator as reference like v0?
I would be very happy with δ. I still think it's the best and unambiguous answer to the question "How big was the curve that Baumgartner saw?" Am I wrong?
Moreover I have a worry on my mind. If some pedantic flat-earther checks the angular size of the sagitta in Metabunk and Bislin calculators, he may find three (or four) different values. That's where the cry begins: THEY even contradict themselves!