Comparing flat Earth and spherical Earth from a geometric point of view

[Pertti Niukkanen]

FlatEarth.ws has an article called "The Reason We Cannot See Earth's Curvature When Standing on a Beach", https://flatearth.ws/standing-on-a-beach. There is an example where the observer height is 2 m and the field of view is 65°.

Putting these values into Walter Bislin's calculator we must notice that in the View∠-box is the diagonal FOV. But 65° is the horizontal FOV. So you must type into the View∠-box the value 65*1.2018502 = 78.1203. http://walter.bislins.ch/bloge/inde...6-9-9-9-6~0.0343-10-11013.0098-114.987-9-31-1

Without refraction, we get the values as follows:

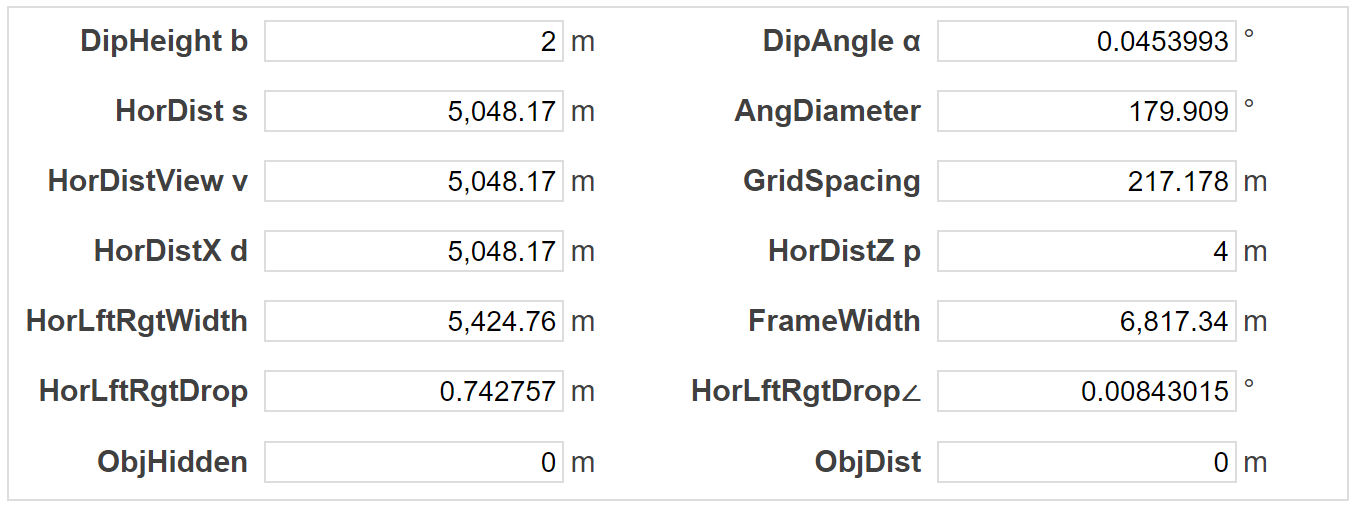
These calculations in the FlatEarth.ws -article are correct:
– Distance to the horizon = 5048 m (HorDistView v)
– Length of the visible horizon = 5425 m (HorLftRgtWidth)

The visible bulge (sagitta) of the horizon (HorLftRgtDrop) is 0.742757 m. But FlatEarth.ws says, "If the length of the horizon is 5048 m, then the bulge in the middle is 0.577 m." This is clearly not correct.

The bulge calculated by FlatEarth.ws is the sagitta of the circular segment of the Earth's great circle when the chord is 5425 m. You can see this with the Metabunk calculator when the distance is 5.425 km:
"Sagitta (or 'Bulge') is the amount of rise of the earth's curve from a straight line connecting two points on the surface. 'Sagitta' r-sqrt(4*r*r - d*d)/2, = 0.58 meters", https://www.metabunk.org/curve/?d=5.425&h=1000&r=6371&u=m&a=a&fd=60&fp=3264

This is the sagitta we have been talking about when trying to show the curvature of the Earth. It does not depend on the observer. The horizon bulge (HorLftRgtDrop) is the sagitta of the horizon ring, seen at a certain height above the center of the ring. These are two different things.

In this example the "Earth curve sagitta" is 58 cm and the "Horizon curve sagitta" is 74 cm. They are almost the same. So the sentence in the meme is right: "The bulge is only about 0.01% the length of the visible horizon". However, the reasoning is wrong.

At the observer height 5 m we get the chord 8577 m and the horizon curve sagitta 1.86 m. Then the bulge is about 0.02% the length of the visible horizon. Yet we might say that the conclusion is true: "We can't see Earth's curvature from the Earth surface itself, not because "there's no curvature", but because the curvature is too small for us to perceive."

Ultimately, the conclusion is based on a misconception that confuses the "Sagitta of the Horizon curve" with the "Sagitta of the Earth curve". So FlatEarth.ws should correct the meme and the article, especially since Erik Yde Lauritsen pointed out the error in the comment section already four years ago. (Although I don't know where he gets the bulge 62.6 cm from, instead of 74.3 cm.)

 

[Pertti Niukkanen]

When looking at the horizon, you're looking at a circular ring in which you are at the center (more precisely, slightly above the center). You can compare this to a hula hoop. When you raise the hoop to eye level, you won't see any curvature. When you lower the hoop to the level of your chest, you will see it curved – and most importantly, you will see the same curvature in every direction. But if you look at a hula hoop standing upright against a wall, you'll see the hoop continue to curve as you move your head.

So when you look at the horizon, you are not looking at the curved great circle of the Earth, but at the horizon circle, in the middle of which you are standing. If you look down (in the depth direction), you can see the real curved surface of the Earth, but it is difficult to calculate this curvature directly.

On the left in the picture the red man is watching at the curving horizon. He is standing on a spherical cap. It's easier to see the curving of the horizon if we cut that cap off. The "Sagitta of the Horizon curve" is marked with the letter k. On the right in the picture is demonstration how difficult it is to see the "Sagitta of the Earth curve" s directly.

Suppose the red man above looking at the horizon would only see a small part of the horizon and nothing else. He may remember the old exercise in school geometry: "Given an arc of a circle, complete the circle". But if he doesn't know where he is, he doesn't know in which plane the arc is either.

Below is another example. There is the home curve of the running track. A small part of it is lit with LEDs. In complete darkness, the gray man can only see this part of the arc, so he can complete the circle in many ways in his mind. He may imagine seeing a large circle in front of him.

Perhaps the natural way for a human is to see the circle as standing perpendicular to the gaze. In this example the gray man's interpretation was wrong but also human. So maybe the misconception on FlatEarth.ws site is a human error too.
---------------------------------

@Rory. Some of these images are probably from your video that is no longer available. So thank you!

 

[Mendel]

Truthly McTruthface demonstrates horizon curve for a planet with a radius of 1.31 miles and a surface area 1/3 the size of Washington DC:

Source: https://m.youtube.com/watch?v=8UhMLpbS8xY

 

[Pertti Niukkanen]

Truthly McTruthface demonstrates horizon curve for a planet with a radius of 1.31 miles and a surface area 1/3 the size of Washington DC:

Truthly's video is aptly titled "The Flat Earth Video That NO ONE Can Debunk!", because there is nothing to debunk. Its purpose is somewhat obscure. Is it a clever parody, is it mocking the FE people, or is it a real invitation for them to study and "beat them at their own game"?

Truthly's YouTube career three years ago is quite short. In two months, he released five videos. The one mentioned here is the first one. It has 18758 views. The last one has only 248 views. https://www.youtube.com/channel/UCsK8WJ9VEVkTNNLNiI3QQsg

Maybe the call to study science was too much for FE people, or maybe Truthly himself got bored with the subject. Anyway, I think he is not a genuine flat-earther, but a mere troll is he neither. I especially liked his example using miniature model of the Earth. He could be an inspiring science teacher with his demonstration skills.

 

[Pertti Niukkanen]

A miniature model of the Earth can show many geometric features and optical phenomena of the real Earth. (Unfortunately, the same cannot be said for its ability to describe gravitational phenomena.)

Let's say that the Earth model is made on a scale of 1:10,000. In this model, the radius is 637.1 m and a 180 cm tall person is 0.18 mm.

A ball with a radius of 637 m is impossible to build. So is a hemisphere or a dome, though there are buildings taller than it. But to demonstrate what I have in mind, we need only a spherical cap of the ball.

A circular area on the Earth with diameter of 1100 km has the sagitta of 23.78 km (for example the circular area on US map below). In the model this cap's diameter is 110 m, the radius 55 m and the sagitta 2.378 m.

Let's say we are building a round Science Center (building with a circular ground plan). The roof of this building is the aforementioned spherical cap with a diameter of 110 m (see image below). In the drawing, the height of the building is about 25 m. This number is unimportant. The important thing is that the shape and size of the roof cap are geometrically exactly right.

In the center of the building will be an elevator that takes the visitor to the roof. There, the visitor can make observations about the distance and curvature of the horizon, hidden heights, etc. Refraction is not a problem as it is in the real world. Perhaps the scale equivalents are also quite easy to remember: 1 km – 10 cm and 10 m – 1 mm.

These science centers are being built all over the world all the time. Maybe some architect will be interested in this roof idea. But what exciting or educational experiences could such a roof offer? I have some ideas, but better to leave them for later.
-------------

Where did I get the roof diameter value of 110 m? It's just the diameter of Globen's "dome". Globen (officially Avicii Arena) is a sports arena in Stockholm. It is the largest hemispherical building on Earth. https://en.wikipedia.org/wiki/Avicii_Arena.

As a miniature model of the Earth, Globen is too small (radius = 55 m) for simulations of hidden heights, etc. For these purposes, the roof of the Science Center is much better (radius = 637 m), although it is only a small spherical cap (and not a hemispherical building like Globen).

 

[Rory]

One nice demonstration I did was to take a long piece of flexible plastic (about 5 metres long) and use it to recreate a photograph of mountaintops. When the plastic was flat the scale model mountain peaks didn't match the photo, but when it was curved by the appropriate amount they did.

Unfortunately the video I made is lost but I think there may be some photos somewhere.

 

[Pertti Niukkanen]

Some more thought of the Science Center model. Here are examples of the scale:

Man on the beach
– Earth: Eye height 2 m, Horizon distance 5.05 km
– Model: Eye height 0.2 mm, Horizon distance 50.5 cm

On top of the skyscraper of the future
– Earth: Eye height 1 km, Horizon distance 112.9 km
– Model: Eye height 10 cm, Horizon distance 11.3 m

Airplane
– Earth: Eye height 10 km, Horizon distance 357 km
– Model: Eye height 1 m, Horizon distance 35.7 m

Felix Baumgartner's jump
– Earth: Eye height 39 km, Horizon distance 706 km
– Model: Eye height 3.9 m, Horizon distance 70.6 m

ISS
– Earth: Eye height 408 km, Horizon distance 2316 km
– Model: Eye height 40.8 m, Horizon distance 231.6 m

The "Man on the beach" example has to be left out because the eye height of 0.2 mm is certainly too small to adjust. Also, Felix Baumgartner's jump and ISS have to be excluded because they have horizon distances greater than the roof radius. (To get a horizon distance of 55 m, the height of the eye should be about 2.38 m. This is the same as the sagitta of the roof!).

Let's view the skyscraper example.

Let's say you are looking at the sea from an eye height of 1000 m. A very large ship is heading towards the horizon. The height of the ship is 100 m. (This height is about as much exaggerated as the height of the skyscraper.) You see the ship on top of horizon at the distance of 112.9 km. Then it starts to disappear from the bottom up. At a distance of 148.6 km, it is completely out of sight. If the ship stops right there, you can see it in its entirety again if you rise to 1733 m (by helicopter?)

In the model, the height of your eye is 10 cm and the height of the ship is 1 cm. The ship is on the top of the horizon at a distance of 11.3 m. It has completely disappeared at a distance of 14.9 m. If you stop it there, you can see it wholly again at eye height of 17.3 cm.

These are the numbers that the globe model gives. But the goal is to verify them with your own eyes. So there must be a very precise mechanism that can be used to adjust the viewing height and the movement of the "ship". In order to see the small ship clearly, you must have also some kind of telescope connected at the viewing height adjuster. (You can also use larger ships).

Maybe there's a computer that tells the ship's distance. You can stop the ship's movement by pressing a button, for example when you see it on the top of horizon. Then the computer tells you the distance and gives also the reference number calculated by globe model, so you can compare them.

A sceptical flat-earther can be given the opportunity to go on the roof and measure the distances with his own measuring tape. There is also a Nikon P1000 available, with which he can try to zoom the half-lost ship back.

In this example the horizon is at a distance of 11.3 m and the ship vanishes at a distance of 14.9 m. Yet the horizon looks completely flat. Is this proof that the roof is shaped like a paper towel roll? No, and neither is the Earth.

 

[Mendel]

Some more thought of the Science Center model.

For a more modest investment, buy some flat desert (e.g. outside of Las Vegas?) and landscape it into the desired shape.

Drawbacks: no refraction.

 

[Pertti Niukkanen]

For a more modest investment, buy some flat desert (e.g. outside of Las Vegas?) and landscape it into the desired shape.

It crossed my mind too.

 

[Pertti Niukkanen]

Concorde's maximum cruising altitude is about 18000 m. Putting this value into Bislin's curve calculator, you get the following values with a horizontal FOV = 60° (http://walter.bislins.ch/bloge/inde...66937-9-9-9-6~0.0343-275.049988-1~56.5-9-31-1)

Now the DipHeight b = 17949.3 m. This is the drop (the amount the curve of the earth drops away from horizontal level) at the horizon distance d. It is also the same as the sagitta of the Earth curve at the chord length 2d. (HorDistZ p = b+h. So I think this value is a bit redundant.)

At the distance of the horizon, the drop (and the sagitta) seems to be very closely the same as the height of the observer. This is quite interesting.

I made a calculation to compare the length/sagitta ratio. Here I marked, as before, the sagitta with the letter s. The simple formula below in the red frame gives the ratio h/s as a function of the horizon distance d (HorDistX d).

The table lists some h/s (=h/b) ratios. For example, Concorde's height is about 0.3% larger than the sagitta.

d –––––––––––– s ––––––––––– h –––––––––– h/s
1 km –––––––– 0.08 m –––––– 0.08 m –––––– 1.0000000
5 km –––––––– 1.96 m –––––– 1.96 m –––––– 1.0000003
20 km –––––– 31.39 m ––––– 31.39 m –––––– 1.0000049
50 km ––––– 196.20 m –––– 196.21 m –––––– 1.0000308
200 km ––––– 3.140 km –––– 3.142 km ––––– 1.0004931
350 km ––––– 9.621 km –––– 9.636 km ––––– 1.0015124
478 km ––––– 17.96 km –––– 18.01 km ––––– 1.0028265 (Conc.)
700 km ––––– 38.57 km –––– 38.81 km ––––– 1.0060912 (Baum.)
1500 km ––– 179.10 km ––– 184.28 km ––––– 1.0289247
2177 km ––– 383.49 km ––– 408.05 km ––––– 1.0640478 (ISS)
3000 km ––– 750.53 km ––– 850.76 km ––––– 1.1335358
4000 km ––– 1412.2 km ––– 1814.4 km ––––– 1.2847881

During his 39 km jump, Felix Baumgartner saw the horizon about 700 km away. The drop at this distance is also about 39 km. If he had said, "The drop at the distance to the horizon is the same as my altitude", he would have made only a 0.6% error.

If an astronaut on ISS said the same thing, he/she would make a 6% error. But there the distance to the horizon is about 2200 km. At small distances sagitta s (= drop b) and the observer's height h are practically the same.

 

[deirdre]

One nice demonstration I did was to take a long piece of flexible plastic (about 5 metres long) and use it to recreate a photograph of mountaintops. When the plastic was flat the scale model mountain peaks didn't match the photo, but when it was curved by the appropriate amount they did.

Unfortunately the video I made is lost but I think there may be some photos somewhere.

you lost your youtube account? jeez. there is another demo in that thread, you had linked
does it work?

https://www.metabunk.org/threads/ex...rate-the-shape-of-the-globe.10309/post-229834

 

[Rory]

you lost your youtube account? jeez.

Yep, been gone over 2.5 years. A linked account I had got a couple of copyright strikes and everything connected to it was terminated. Supposed to be three strikes before they do that but all attempts to communicate with them hit brick walls.

there is another demo in that thread, you had linked
does it work?

https://www.metabunk.org/threads/ex...rate-the-shape-of-the-globe.10309/post-229834

Yep, that's the one. Has Bobby Shafto's version and some details of mine, including scale and spreadsheet with the calculations. Thanks for finding.

 

[Pertti Niukkanen]

A couple of days ago we had the September equinox. On equinoxes, night and day are of equal length everywhere on Earth. On the June solstice, the day is longest in the Northern Hemisphere (and shortest in the Southern Hemisphere). On the December solstice, the situation is vice versa.

How do observers at different latitudes see the Sun's path across the sky on these special days? How do they see it if the Earth is flat?

The left picture shows the paths of the Sun at latitude 40° according to the globe model. (Note: 50 = 90 - 40, 73.4 = 50 + 23.4, 26.6 = 50 - 23.4).

The right picture shows the "semi-official" FE model. In this model, the Sun has a diameter of 50 km and a height of 5000 km. The Sun orbits between the tropics. When the path is in the Tropic of Cancer, it is midsummer in the North, when it is in the Tropic of Capricorn, it is midsummer in the South.

I made a "dynamic" model based on the left image. The model is easy to build yourself (and this time the investment is modest ). You basically just need a transparent hollow plastic ball, different colored markers and colored water.

1
Draw a great circle on the ball and small circles on both sides of it, as if you were making a globe with equator and tropics drawn on it. Drawing "tropics" is helped by the knowledge that their distance from the "equator" is approx. 41% of the radius of the sphere. So if the radius R of the ball is 10 cm, the arc a is approx. 4.1 cm.

Then drill a hole on the "equator" big enough to fill the ball with water. Reserve a cap that fits into the hole (e.g. rubber cap witch tapers slightly at one end).

2
Then fill the ball in half with water. You can color the water with e.g. caramel color. Press the cap firmly into the hole. Turn the ball so that the cap is exactly at the "zenith". Now you can see what the Sun's paths look like from the equator on equinoxes and solstice days. You can see situations at other latitudes by tilting the ball in the direction of the orange arrow.

3
The tilt angle directly corresponds to the observer's latitude. By tilting 70 degrees, you can see the situation at latitude 70 (for example Nuiqsut, Alaska or Utsjoki, Finland). You will notice that during the summer solstice the Sun does not set there at all. During the winter solstice, it does not rise at all.

The situation in the southern hemisphere is obtained by tilting the ball in the opposite direction. For example, by turning the globe 70 degrees "counter clockwise", you can see the situation at latitude -70 (somewhere on the edge of Antarctica). In this case, the red circle has completely emerged from the water and the pink one has sunk under the water. That is, during the summer solstice, the Sun does not rise at all, and during the winter solstice, midnight Sun prevails.

This model shows the paths of the Sun only on equinoxes and solstice days. Adding more circles that correspond other dates is possible, but it could make the model quite messy. The path of the Sun on other dates can roughly estimate by comparing with these three circles.

The ball would need some kind of stand, so that the tilting in the right direction and right amount of degrees would be possible. If somebody actually build this model, it would be nice hear about it.

 

[Mendel]

How do observers at different latitudes see the Sun's path across the sky on these special days? How do they see it if the Earth is flat?

My favorite low-tech globe proof is tracking the tip of the shadow a sundial on (or near) equinox and see it teack a straight line—impossible if the sun moves in a circle above flat Earth.

See https://www.metabunk.org/threads/ho...t-relying-on-nasa-or-photos.10557/post-229547 for a description and a video explainer.

Post 24 in that thread describes a paper sundial. If you align it correctly (parallel to the equator), it shows you ghe rotation on any day, not just the equinox.

 

[Pertti Niukkanen]

My favorite low-tech globe proof is tracking the tip of the shadow a sundial on (or near) equinox and see it teack a straight line—impossible if the sun moves in a circle above flat Earth.

Thanks for the link. The videos of Flat Earth Math all seem to be great. https://www.youtube.com/c/FlatEarthMath/videos. The shadow forming a straight line at the equinox was a new thing to me. I hadn't thought about that, although I knew that all places on Earth are at the center of the Sun's circular path at the equinox.

One may wonder why the gnomon does not stand in the middle. It doesn't matter as long as its tip is in the plane of the Sun's path. (You can also get the gnomon's place to the center as a sort of "limit value". See the picture above right.)

I immediately wanted to try this in practice because the autumnal equinox is still very close. Unfortunately, it was cloudy in Helsinki. Maybe tomorrow will be better.

The whole thread was interesting. I have to try Bislin's paper sundial also, at least next summer. (Last summer I made my FE sundial, maybe I'll tell about it later.)

I especially liked what Mick West said:

"I really think that asking someone to explain things isn't going to work here - they will just assume there's a FE answer that they don't understand, exactly like there's a globe answer that they also don't understand. You have to be able to show them stuff in an accessible way. What do they actually understand? What can they understand?"

It seems that everything essential has already been said in 2019. However, Mick's challenge is still relevant: "You have to be able to show them stuff in an accessible way". So maybe it's worth repeating old stuff. Maybe some new point of view is important to someone. At least this is my pious hope.

 

[JMartJr]

Jos Leys's video on sundials and the shape of the Earth is quite nice. As are all his videos... if you are not familiar with them, I commend them to your attention.


Source: https://youtu.be/OYZ-Ab9-WHI

 

[Pertti Niukkanen]

Jos Leys's video on sundials and the shape of the Earth is quite nice. As are all his videos.

Yes, they certainly are.

In FE discussions, I've often linked to some of Leys' videos, because I think it solves the question visually right away. Rarely (if ever) have I received any comments from flat-earthers.

Mick West said in the thread mentioned above:

"I know quite reasonable people who do not know how an eclipse works in the conventional model. I think that's actually too advanced a topic for the average person, and certainly too advanced for someone who has not really done anything with geometry for decades (if ever)."

I'm afraid that Leys' videos are just fun animations for the FE audience (and some other lay people as well) with no connection to their questions. So this stuff is not accessible to them. To understand the value of Leys' videos, one must have some basic knowledge of geometry and astronomy. I think this is not too much to ask of a true truther.

Of course, I'm a layman myself. I've been wrong many times (even in basic things). However, I have always received the correction here. In the old threads, I have also found answers to questions that have bothered me for a long time. This is the strength of the Metabunk forum. Questions are not left hanging, but are answered (if there exists an answer).

 

[Pertti Niukkanen]

Today it was sunny in Helsinki. So I made the Mendel's favorite test on my balcony. As the pointer (gnomon) was a marker pen. I marked the tip of the shadow directly on the surface of the table.

I made five observations at fairly random intervals. The last one was at 16:14 Helsinki local time. Then the table ran out.

The five marks did indeed line up roughly on the same line (see the picture on the right). Even this sloppy qualitative test is enough to prove the globe to me. Of course, it should be done with better equipment and better documentation on exactly the right day. Maybe next spring…

 

[Pertti Niukkanen]

On equinoxes at the equator, the Sun rises precisely in the east, passes through the zenith and sets precisely in the west. This could have been seen a couple of days ago, e.g. at Equator Meru in Kenya (0.00, 37.66).

On the FE map, the Sun moves in a circular path above the equator on equinox days. If its orbital speed is constant, it will move half a revolution forward in the time between rise and set.

Viewed from Meru (point M), the Sun rises at point A and sets at point B. So it rises from the northeast and sets in the northwest. During its journey, it is newer seen in the east or west direction.

In this FE model, the height of the Sun is always approx. 5000 km and its diameter is approx. 50 km. From this information, we can calculate how the Sun is seen from Meru on the equinoxes.

The sunrise in Meru means that the Sun appears suddenly as a small point (angular diameter approx. 0.19 degrees) in the north-eastern sky at an altitude of approx. 20 degrees above point A. From there it continues its course until it is exactly at the zenith above Meru, where its angular diameter is approx. 0.57 degrees (i.e. the same order of magnitude as in the globe model). Then the Sun continues along a circular arc until it disappears above point B in the northwest direction at an altitude of approx. 20 degrees with an angular diameter of approx. 0.19 degrees (= 11.5 arc minutes).

In fact, the previous representation contradicts what Samuel Rowbotham says about the vanishing point and the resolution of the eye. According to him, the object disappears when its angular size is smaller than 1 arc minute. However, when the sun appears in the Meru sky, its angular diameter is about 12 arc minutes, so it should have been visible much earlier. Well, I guess Rowbotham's estimates weren't very accurate. He once calculated that the Sun is only a good thousand kilometers above the Earth.

You may also wonder how the Sun shining above Meru at an altitude of 5000 km can illuminate exactly a semicircle of the FE disc. The picture above right is from Jos Leys' excellent video "Sunlight over a flat Earth: Debunked!"


Source: https://www.youtube.com/watch?v=fEYsgP4CuSA

 

[Mendel]

Even this sloppy qualitative test is enough to prove the globe to me. Of course, it should be done with better equipment and better documentation on exactly the right day.

I love this experiment precisely because it doesn't need "better equipment" or quality documentation: all it requires is a gnomon, a flat surface, a way to mark it, and the time to check it a few times during the day—and some sun. Everyone can find their own way of setting it up with what they have at hand. And it doesn't even need to be on the equinox exactly! You can be sloppy, and it still works!

My own setup with the camera time lapse is already the "luxury version". If I did it again, I'd add a compass, to show that the line is east-west aligned.

The fun part is that the prediction of this experiment, the straight line, is both unexpected and beautifully simple: it's hard to come up with, but easy to confirm.

 

[Pertti Niukkanen]

If I did it again, I'd add a compass, to show that the line is east-west aligned.

That would be a really good addition to the test. Unfortunately I don't have a decent compass. However, I could have easily seen the south-north direction by making one observation exactly at noon.

Solar noon was yesterday in Helsinki at 13:11 local time. My observation 2 is made at 12:47. If I had waited 24 minutes the shadow would have been exactly in south-north direction. I could have drawn this line on the table. At the end of the test, I would have seen that this line is perpendicular to the line formed by the five marks. I'll have to remember this next time.

 

[AmberRobot]

On equinoxes at the equator, the Sun rises precisely in the east, passes through the zenith and sets precisely in the west. This could have been seen a couple of days ago, e.g. at Equator Meru in Kenya (0.00, 37.66).

On the FE map, the Sun moves in a circular path above the equator on equinox days. If its orbital speed is constant, it will move half a revolution forward in the time between rise and set.

Viewed from Meru (point M), the Sun rises at point A and sets at point B. So it rises from the northeast and sets in the northwest. During its journey, it is newer seen in the east or west direction.

In this FE model, the height of the Sun is always approx. 5000 km and its diameter is approx. 50 km. From this information, we can calculate how the Sun is seen from Meru on the equinoxes.

The sunrise in Meru means that the Sun appears suddenly as a small point (angular diameter approx. 0.19 degrees) in the north-eastern sky at an altitude of approx. 20 degrees above point A. From there it continues its course until it is exactly at the zenith above Meru, where its angular diameter is approx. 0.57 degrees (i.e. the same order of magnitude as in the globe model). Then the Sun continues along a circular arc until it disappears above point B in the northwest direction at an altitude of approx. 20 degrees with an angular diameter of approx. 0.19 degrees (= 11.5 arc minutes).

In fact, the previous representation contradicts what Samuel Rowbotham says about the vanishing point and the resolution of the eye. According to him, the object disappears when its angular size is smaller than 1 arc minute. However, when the sun appears in the Meru sky, its angular diameter is about 12 arc minutes, so it should have been visible much earlier. Well, I guess Rowbotham's estimates weren't very accurate. He once calculated that the Sun is only a good thousand kilometers above the Earth.
View attachment 54964

Yes. That picture on the left basically destroys the flat earth model. Whatever you think about the globe model, the movement of the sun in the sky demonstrates that this model of a flat earth is flat out wrong. And the sun's movement can be watched and measured by any human on earth.

You may also wonder how the Sun shining above Meru at an altitude of 5000 km can illuminate exactly a semicircle of the FE disc. The picture above right is from Jos Leys' excellent video "Sunlight over a flat Earth: Debunked!"


Source: https://www.youtube.com/watch?v=fEYsgP4CuSA

This video isn't particularly compelling because all it does is apply the results from a globe model to a flat earth. If you don't believe the globe model is right then this presentation carries no actual power. As relatively easy as it is to demonstrate a globe earth model, it's almost trivially easy to demonstrate the falsity of the flat earth model.

 

[Pertti Niukkanen]

How does a sundial work in the standard FE model? JMartJr linked a video by Jos Leys "Debunking flat Earth using only a stick" (see https://www.metabunk.org/threads/co...metric-point-of-view.12591/page-2#post-280310). There, Leys proposes a simple experiment to solve the matter, although he is certain of the outcome: Nothing but circles!

Surely Leys' simple test is enough to debunk the FE model. Last summer, however, I made a more accurate sundial model for the flat Earth. I can't resist telling you about it. Maybe it's a fun craft.
==================

First I modeled a sundial for the southern hemisphere. As the installation location I chose point A (coordinates -70,-65) on the Antarctic Peninsula (picture 1). The map shows also the Tropic of Cancer and the Tropic of Capricorn. In the FE model, the Sun at an altitude of 5000 km moves along the Tropic of Cancer at the summer solstice on June 21. and along the Tropic of Capricorn at the winter solstice on 21.12.

What kind of shadow would the stick at point A (blue arrow in pictures 2 and 3) cast? The shadow of light travelling in a circle is also a circle on a parallel plane. So we can conclude that the circular paths of the Sun at the solstices appear on the flat plane as circles drawn by the shadow of the tip of a stick. The circles have the same center, and the ratio of the radii remains the same regardless of the length of the stick. The length of the stick determines the size of the circles.

The sundial must be made separately for each latitude (just like on the Globe). For this, you need to calculate the distance of the installation place from the North Pole (marked with the letter d). You can do it with a formula d = ((90-φ)/360)*40008, where φ is the latitude of the installation site. For example, the distance of point A from the North Pole is 17781 km (see picture 2).

Now we have the necessary information from the FE model:
– Height of the Sun 5000 km (constant)
– Radius of the Tropic of Cancer 7406 km (constant)
– Radius of the Tropic of Capricorn 12610 km (constant)
– The distance of the installation site from the North Pole 17781 km (calculated)

The dial with the stick is similar with the pattern on the map (mirror image). The sundial thus has the same ratios as the FE reality. The height of the sun corresponds to the length of the stick. If we scale the dimensions of the sundial so that the length of the stick is 100 cm, the radius of the small circle (Tropic of Cancer) is 148 cm, and the radius of the larger circle (Tropic of Capricorn) is 252 cm. The distance of the stick from the center of the circles is 356 cm and it must be measured in the north direction. (Figure 2 is calculated using similarity.)

Picture 3 shows the finished sundial set up at location A. The length of the blue arrow (the gnomon) is proportional to the size of the circles.

The hour scale on the dial is evenly spaced. This follows from the fact that the Sun's orbital speed during one day can be considered constant. During the year, the orbital speed does change, but the angular speed remains the same (it is always 360 degrees in a year).

The hour readings increase clockwise, because the FE Sun also rotates clockwise (viewed from above). This is happening everywhere on the flat Earth. (On spherical Earth, the hour readings increase clockwise in the northern hemisphere and counter-clockwise in the southern hemisphere.)

A couple of examples of reading the sundial:

- At the winter solstice, the tip of the shadow follows the outer circle. The tip of the arrow (a) hits the 17 hour position. At approximately 13:40, the direction of the arrow is the same, but the arrow is shorter. Thus, the direction of the shadow does not alone determine the time. The length of the shadow is also needed. So the most important thing is the location of the tip of the shadow.

- At the summer solstice, the tip of the shadow follows the inner circle. The tip of the arrow (c ) hits the 3 hour position. At approximately 10:45, the direction of the arrow is again the same, but the arrow is shorter.

So the FE sundial seems to work just fine in solstice days. Are separate circles needed for other times between these circles? In Figure 3, the tip of the arrow (b) hits a circle that is not marked on the dial (dashed line). Still, it works in this case too. You just have to estimate the time on the dial. It seems to be approximately 14:30.

The sundial takes care of the season by expanding and shrinking the circle automatically. You can roughly estimate the current month from this circle. From the arrow (b), you could estimate that the summer solstice is about a month and a half away – ahead or behind.

Short practical instructions to set up the FE sundial:

1) Using the latitude of the setup site, calculate the length d (formula in figure 2)
2) Divide the number you get by 50. This way you get the distance of the stick from the center of the circles to the same scale, where the length of the stick is 100 cm and the radii of the circles are 148 cm and 252 cm.

For example, in Melbourne (latitude -37.8) we get d = 14203. This is 284 divided by 50. Now you can draw two concentric circles with radii of 148 cm and 252 cm on flat plane. Then measure 284 cm directly north from the center of the circles and set up a 100 cm stick on it. The sundial is ready.

If your FE friend in Australia thinks this sundial is too large for his backyard, he can easily reduce its size. If your friend has some stylish stick with a length of e.g. 43 cm, he can use it. The other dimensions just need to be shortened in the same ratio, i.e. by multiplying by the number 0.43. In this case, the radii of the circles are 64 cm and 108 cm, and the distance of the stick from the center is 122 cm.
==================

If you find the whole project idiotic and my long explanations extremely boring, I can't blame you. Did I even build the FE sundial myself? Yes, I did.

 

[Pertti Niukkanen]

Last summer I indeed made a FE sundial for Helsinki (60,25).

1) The formula d = ((90-φ)/360)*40008 now gives d = 3334. Dividing this number by 50 we get about 67.
2) Draw two concentric circles on a flat plane, the radius of the smaller one is 148 cm and the radius of the larger one is 252 cm.
3) From the center of the circles, measure exactly 67 cm in the north direction (the number calculated above). Then place there a thin straight stick vertically. Its height from the ground level must be exactly 100 cm.

Actually, I didn't build the dial full scale (nor set it up on a neighbour auntie's backyard). I reduced it considerably so that the stick was only 3 cm long.

I did my "balcony tests" on June 19, 2022, which is very close to the summer solstice. For comparison, I made also a sundial based on the globe model. The easiest one is an equatorial sundial, where the gnomon is perpendicular to the hour disc. My simple version needs only an empty cottage cheese jar and a knitting needle.

The shooting time given by the camera is marked in black text on the pictures. The solar time is in red. This is obtained from the information that solar noon was at 13:21 Helsinki local time. Since both "clocks" show solar time, the time they give should be "the red time".

By examining the series of pictures, you can see that the "jar dial" gives the correct solar time quite accurately.

The FE dial, on the other hand, is in trouble. It was so close to the summer solstice that the tip of the shadow should follow the inner circle. However, it doesn't do that, as you can already see from the first picture.

As noon approaches, the solar time displayed by the FE dial approaches the correct one. At noon (picture 13:20/11:59) the dials show practically the same solar time. The direction of the shadow is correct in both dials, because according to the FE model, the Sun is in the south at noon also. The length of the shadow is also almost correct in the FE dial. This is due to the fact that the elevation angle of the Sun is almost the same in Helsinki at summer solstice in both models. In the Globe model it is approx. 53° and in the FE model approx. 51°.

Later the jar dial still works fine, but the tip of the shadow in FE dial has strayed from the inner circle again. Over time, this phenomenon will only grow. Actually the tips draw a hyperbola. The picture in red frame shows the tip marks together. With a little goodwill, you might see that they form a hyperbola. (Sorry for the gap in observations in the afternoon. I fell asleep.)

Of course, this result was not a surprise. I'm sure my FE sundial would work if the FE model is correct. If light behaves in some strange way (as flat-earthers may claim), why doesn't it affect the globe model sundial next to the FE sundial? So there are no excuses. The FE model is not correct.

Is the test worth doing? With a FE friend, it could be. Anyway, it was fun summer crafting.

 

[FatPhil]

If you ever need to do an experiment which requires one person to be at the top of Torni in Helsinki tooking south, and another to be in Horizont in the Swissotel in Tallinn looking north - for science! - just let me know!

 

[Pertti Niukkanen]

This video isn't particularly compelling because all it does is apply the results from a globe model to a flat earth. If you don't believe the globe model is right then this presentation carries no actual power.

Leys' video is indeed completely in accordance with the globe model. The border between night and day is only shown on the AE map. Everyone can verify these natural phenomena with their own eyes or with the help of the TimeAndDate site.

David Weiss (aka DITRH) probably knew this too when he made his "Flat Earth Sun, Moon & Zodiac Clock" app. Below is a comparison of Weiss' app and Leys' video 1) Near summer solstice, 2) Near winter solstice.

On Leys' video, the boundaries of the illuminated area are sharp, in the app they are blurred. More important difference is that the entire Antarctic continent is missing. Why is it missing even though it's on Gleason's classic FE map? Perhaps the removal of Antarctica was intended to avoid questions about the midnight sun in the south (picture 2).

So David Weiss accepts the information from the TimeAndDate website, which of course matches the video by Jos Leys. However, this doesn't disturb Weiss as he apparently has an explanation. The solution is presented in the video "Day and Night on a Flat Earth DEBUNKED?", of which a couple of pictures below.

Picture 3 is especially interesting. It shows the situation during the winter solstice, when the spotlight of the Sun is really special. It illuminates the entire flat Earth, but leaves a dark hole in the middle.

Weiss' "explanation" in his video is an analogy with the behavior of light in a thick convex lens. He illuminates the lens with a penlight and, by moving the pen, makes light and shadow patterns roughly similar to those in his app or in Leys' video.

Whatever Weiss's explanations, with this video he has denied the traditional FE notion of the impossibility of the midnight sun in Antarctica.

Weiss introduces the video:
"Globe zealots will have you believe that the day and night patterns are impossible on a flat earth when in fact that makes plenty of sense. The optics of the sky are very complicated and are not needed to prove the earth is obviously and observably flat and stationary."

In the comments, he also says:
"Actually there are two domes. Our personal viewing Dome and possibly the real dome. The real sun can be within the real Dome and we see the apparent Dome within our personal viewing dome."

With these imaginative loose statements, he gives the old-fashioned flat-earthers a chance to get over the contradiction that admitting the nightless nights in Antarctica could cause. Leys' videos cannot break such a defence. Nor any other rational arguments.

Day and Night on a Flat Earth DEBUNKED?

Source: https://www.youtube.com/watch?v=zvVXxfkyX1Q&feature=youtu.be

 

[Pertti Niukkanen]

Earlier I described what a FE sundial would be like in Melbourne. Let's take another look at how an observer in Melbourne would see the Sun's path in the sky.

The picture shows observer M in Melbourne (-37.8, 145.0) watching the Sun. According to the FE model he sees the Sun's path as an ellipse in the northern sky. This happens every day year after year.

The ellipse is smallest on the summer solstice June 21. From there it begins to grow as the Sun draws an expanding spiral. The ellipse is widest on the winter solstice December 21. After this the orbit of the Sun is shrinking, and the smallest ellipse is obtained again on summer solstice the next year. Never the Sun is seen in south, east or west.

It's spring in Australia now. The December solstice (midsummer in Australia) is approaching. A few calculations about the Sun in Melbourne on December 21st according to the FE model:

– Maximum distance: 26823 km
– Minimum distance: 1603 km
– Maximum elevation angle: 72.2 degrees
– Minimum elevation angle: 10.6 degrees
– Maximum angular size: 0.55 degrees (32.7 arc minutes)
– Minimum angular size: 0.10 degrees (6.3 arc minutes)

The observer sees the Sun's path as an ellipse in the northern sky. The width of this ellipse is about 90 degrees as seen from M (if I calculated right).

According to TimeAndDate, the sunrise is at 5:54 in the direction 121 ESE (east-southeast). Its direction is East at 9:33 at an altitude of 40 degrees. At noon, the direction is North at an altitude of 76 degrees. The direction is West at 17:01 at an altitude of 41 degrees. The sunset is at 20:41, direction 239 WSW (west-southwest). https://www.timeanddate.com/sun/australia/melbourne?month=12&year=2022

So, According to the GE-model the Sun can be seen in East and West. According to the FE-model this is impossible.

There is midnight, when the Sun's distance is greatest. At that time its angular size is still 0.10 degrees (6.3 arc minutes). Also Sun's elevation angle is 10.6 degrees at midnight.

According to Rowbotham, the Sun would disappear from view when its angular diameter is less than 1 arc minute. So M should very well see the Sun even at midnight. Also the change in Sun's angular size during the day is spectacular. In GE model there is no change.

Everyone living south of the tropic of Capricorn should see this phenomenon. So, if you live in Southern Australia, New-Zealand, South Africa or South America, watch the Sun's path one whole day. Do you see the ellipse in the northern sky?

If you know any flat-earthers in Melbourne (or further south) it would be fun to hear what excuses they have (I'm sure they have).

 

[Pertti Niukkanen]

We debunkers like to ask flat-earthers: How is it possible that the Southern Cross can be seen in a completely different direction when viewed from three different continents at the same time? (Picture is from Professor Dave's video "Destroying Flat Earth Without Using Science - Part 2: The Stars".)

I was looking for a situation where those three people on three continents actually SEE the Southern Cross simultaneously.

Suppose there are three friends living on different continents:
– P lives in Perth, Australia (-31.9518, 115.8622)
– C lives in Cape Town, South Africa (-33.9198, 18.4236)
– R lives in Recife, Brazil (-8.0076, -34.9329)

The friends tried to find out, is it possible for these three cities to have night at the same time? With the help of TimeAndDate site they found that this could happen near the June solstice.

So they chose the common moment, which is according to the local time:
– For P: 21.6.2022, 05:40
– For C: 20.6.2022, 23:40 (C=P-6)
– For R: 20.6.2022, 18:40 (R=P-11)

The globe above shows roughly the night side of the Earth at that chosen moment. The FE map shows the situation according to the FE-model.

In Perth the morning begins to dawn, in Cape Town is roughly midnight and in Recife is early night. So the sky is still dark enough that all three friends can see the stars at that same moment. Can they see the Southern Cross at the same moment? Yes they can. (Pictures are from TimeAndDate.)

This experiment is not difficult to carry out. Unfortunately, the right time for three places is until next summer. Maybe two are enough, e.g. Perth and Cape Town. Then it is much easier to find a suitable time.

A little more thought.

Instead of a constellation, the object of observation could be a single bright star. There is a very bright star in southern sky called Toliman (α Centauri B). Only Sirius and Canopus are brighter.

Below are two pictures from TimeAndDate site. They show how the southern sky looked in Perth and Recife at the above-mentioned common moment. Toliman is in both pictures and you can see also its altitude and direction. I marked the directions on the FE map and made also a sketchy 3D-model of the situation.

You can notice that Toliman appears in a completely different direction when viewed simultaneously from Perth and Recife. This is impossible if we share the same reality. If we all have our "personal viewing Dome", as David Weiss put it, anything might be possible.

 

[FatPhil]

This experiment is not difficult to carry out. Unfortunately, the right time for three places is until next summer. Maybe two are enough, e.g. Perth and Cape Town. Then it is much easier to find a suitable time.

Is there any FE reason why Gibralter and Tashkent should be excluded from the experiment? They're both within the triangle bounded by the three cities you list on the FE map. A failure to see something would be just as much a datapoint as seeing it at the wrong orientation, surely.

 

[Rory]

In the comments, he also says: "Actually there are two domes. Our personal viewing Dome and possibly the real dome. The real sun can be within the real Dome and we see the apparent Dome within our personal viewing dome."

Thank you for posting this. It gave us all a real chuckle here in the casa.

 

[Pertti Niukkanen]

Is there any FE reason why Gibralter and Tashkent should be excluded from the experiment?

Three cities in the southern hemisphere, as far apart as possible, have been a way for the debunkers to dramatize the contradiction. Two cities are equally sufficient. The only condition is that you can choose a moment when night prevails in both cities.

The southern hemisphere is good because you can see the Southern Cross from there. It is close enough to the south celestial pole that everyone sees it roughly in south direction.

You can do the test in the northern hemisphere too. However, it is more difficult because when looking south, there is hardly a bright object near the south celestial pole that everyone could see at the same time. (To get a clear contradiction you must look roughly south.)

You asked about Gibraltar (36.142, -5.356) and Tashkent (41.302, 69.232). They are still so close to each other that the test result will not be very impressive. However, I tried how it works. (Note that being inside the triangle bounded by the three cities in the previous example is irrelevant.)

It is easy to find a moment when it is night in both cities. I chose the common moment, which is according to the local time:
– For Gibraltar: 1.11.2022, 01:00
– For Tashkent: 1.11.2022, 05:00

Then it is night in both places and Sirius, the brightest star in the sky, is visible in the southern sky.

I placed the direction of Sirius on the FE map for both cities. You can see that the directions differ from each other. The difference is very small, only about 3°. Note that the red and blue arrows do not intersect in the line of sight. So the explanation that Sirius could be close to the Earth cannot be true. (Also, the altitudes are different: 8.18° in Gibraltar, 31.50° in Tashkent. They should be the same on a flat Earth.)

Yes, this experiment also debunks the FE theory. However, the evidence is rather weak in the limits of observational accuracy and hardly convinces anyone. It is therefore better to choose e.g. Cape Town and some city in Australia to pair with it.

Then the object of observation can be the Southern Cross or, for example, the bright star Toliman. Finding the same observation time at night is also easy. And everyone can clearly understand the contradiction of the test result with the FE model.

 

[FatPhil]

You asked about Gibraltar (36.142, -5.356) and Tashkent (41.302, 69.232). They are still so close to each other that the test result will not be very impressive. However, I tried how it works. (Note that being inside the triangle bounded by the three cities in the previous example is irrelevant.)

What follows contains no Southern Cross, and therefore wasn't including them in your previously defined experiment.

(And being in the triangle was relevant - I was deliberately ensuring I did not go outside the convex hull for reasons of linearity (every point within the triangle is, by some measure[*], a weighted average of the three corner points), I did not extend the gamut of points that were relevant. I did this because every property being measured is a well-behaved - should be continuous, differentiable, and more importantly defined across the whole gamut - but I was unwilling to assume (even if it's true), that it would remain defined and well-behaved outside that gamut. I was covering our back to not introduce new weird behaviour (like singularities).)

[* 45N is "half way up the globe". 30N is "half way up the globe". Fight!]

 

[Mendel]

[* 45N is "half way up the globe". 30N is "half way up the globe". Fight!]

30⁰N is halfway up the globe.
45⁰N is halfway to the pole.

 

[Mendel]

The southern hemisphere is good because you can see the Southern Cross from there. It is close enough to the south celestial pole that everyone sees it roughly in south direction.

Yes. You can see the Southern Cross from Recife and from Perth. If you cannot see it from Gibraltar, which is halfway between Recife and Perth, what does that mean for the shape of the Earth?

(It means that Recife and Perth must be closer together than the AE map suggests.)

Sending radio across the South Pole should be another way to confirm the pole exists.

 

[Pertti Niukkanen]

Is there any FE reason why Gibralter and Tashkent should be excluded from the experiment? They're both within the triangle bounded by the three cities you list on the FE map. A failure to see something would be just as much a datapoint as seeing it at the wrong orientation, surely.

If you cannot see it from Gibraltar, which is halfway between Recife and Perth, what does that mean for the shape of the Earth?
(It means that Recife and Perth must be closer together than the AE map suggests.)

So I didn't understand Fat Phil's comments and tried to answer some other question. I'm sorry about that. I blame my bad English.

 

[FatPhil]

So I didn't understand Fat Phil's comments and tried to answer some other question. I'm sorry about that. I blame my bad English.

Sinun englantini on parempi kuin minun suomeni! I was trying to keep the question as brief as possible to minimise places for confusion, but instead made it too brief, leaving places for confusion! Anteeksi.

 

[Pertti Niukkanen]

Wednesday 20 March 2024 is the vernal equinox. Then day and night are the same length, because the Sun is on its path at the point where the path (ecliptic) intersects the celestial equator.

The celestial sphere describes well how the starry sky looks from Earth. It appears to revolve around the stationary Earth approximately once a day. This geocentric description is still very useful and makes it easier to observe the starry sky. (It is clear, of course, that the apparent rotation of the celestial sphere around the Earth is due to the Earth's own rotation, but this fact is not important in further analyses.)

Picture 1 shows the southern starry sky as seen in Helsinki on 13.3. at 22:00 with the Stellarium program. Orion is still visible in the southwest. Mintaka, the star to the right of Orion's belt, appears to be located on the equator of the celestial sphere. This is quite precisely the case, because its declination is only approx. -0.28°.

Figure 1 is the view from "inside" the celestial sphere. Picture 2 shows the celestial sphere as seen "from the outside". I have marked the Orion stars Betelgeuse (B), Mintaka (M) and Rigel (R) on it. When seen from outside the celestial sphere, Orion is a mirror image of the "inside view" (cf. the thumbnail on the right). This is also an issue regarding the "handedness" of celestial globes.

It can be said that the positions of the fixed stars on the celestial sphere do not change. (Yes, they also change, but to a perceptible extent only over long periods of time.) The movement of the sun and planets on the celestial sphere, on the other hand, is easy to observe. The position of the sun at the spring equinox is marked in figure 2 with the horns of a ram . Currently, that point (vernal equinox) is actually in the constellation of Pisces, but 3000 years ago it was in the constellation of Aries.

Earth's sidereal day is approx. 23h 56min 4s (i.e. approx. 23.9345 h). This means that in that time the Earth rotates around its axis 360° in relation to the fixed stars. The rotation time of the Earth in relation to the Sun is a solar day, which is exactly 24 hours long. It is therefore approx. 4 minutes longer than the sidereal day. So the Earth rotates in relation to the Sun by 15° per hour, but in relation to the stars it rotates approx. 15.04° per hour ( = 360/23.9345).

Picture series 3 tries to illustrate the situation. The time difference between figures 3a and 3b is one sidereal day. When you compare Rigel's positions in the pictures, you will notice that they are the same. When one solar day d = 24 h has passed, Rigel has clearly moved further to the west (Figure 3c).

(Note. More precisely, above is the mean solar day, because the length of the solar day varies by about a minute during the year. This is again due to the ellipticity of the Earth's orbit. The old definition of the hour was based precisely on the mean solar day, so that the day d = 24 h = 86400 s. The length of the sidereal day, on the other hand, remains very exactly the same throughout the year. So there's no need to talk about a "mean sidereal day".)

If the star is located on the celestial equator (e.g. Mintaka), it always rises exactly in the east and sets exactly in the west. It is at its highest in the south, when its height relative to the horizon is 90° minus the geographical latitude of the locality (e.g. in Helsinki 90° - 60° = 30°). Mintaka's direction changes by 15.04° per hour. Here, by change I mean the angle between the direction vectors. What if the star is located somewhere other than the equator. What then is the angle between the direction vectors?

In Picture 4, I have tried to calculate that dependency. Let α be the angle by which the globe turns around its axis in a certain time t. In this case, the direction of a star located on the equator (e.g. Mintaka) also changes by the angle α in time t (indicated as the angle between the direction vectors).

If the star is "higher", i.e. closer to the north celestial pole, the angle between the direction vectors is smaller than α. In the figure, this angle between the direction vectors a and b is marked with γ. The angle β is the declination of the star (approx. 60° in the picture).

In the figure, the formula in the red frames is derived, which generally gives the angle γ when the angles α and β are known. This can be used to calculate, for example, how large an angle Castor (α Geminorum, see also figure 1) moves per hour as seen from Earth. In this case, α = 15.04° (magnitude of Earth's rotation per hour relative to the stars) and β = 31.84° (Castor's declination). The formula now gives the angle γ = 12.77°.

A couple of other examples of a star's direction changing in one hour:
Star ––––––––––––––––––– Declination ––– Angle γ
Capella (α Aurigae) ––––––– 46.02° ––––––– 10.43°
Dubhe (α Ursae Majoris) ––– 61.62° ––––––– 7.13°
Polaris (α Ursae Minoris) ––– 89.37° ––––––– 0.16°

You can verify these results yourself if you have accurate equipment.

What does all this have to do with the vernal equinox? More on that later.

 

[Mendel]

Wednesday 20 March 2024 is the vernal equinox.

All next week, the track of the shadow of the tip of a gnomon on a flat surface will be approximately straight, because we live on a globe.

 

[Pertti Niukkanen]

Above, I applied the formula to the fixed stars, where α = 15.04° (the magnitude of the Earth's rotation per hour in relation to the stars). The formula can also be applied to the Sun, but in that case α = 15° (the magnitude of the Earth's rotation per hour in relation to the Sun).

The Sun also differs from the fixed stars in that its declination changes during the year. On equinoxes, it is located on the celestial equator, when the declination β = 0°. At the summer solstice β = 23.4° and at the winter solstice β = -23.4°. The variation is due to the angle between the Earth's orbital plane and the equatorial plane, which is approx. 23.4°.

In the table above I have calculated γ-angles for the Sun's declinations between 0° and 23.4°. At the vernal equinox (kt) γ = 15°, as it should be. At the summer solstice (ks) γ = 13.76°. This is a clearly noticeable difference in the change of the Sun's direction per hour at different times of the year. (The change here means the angle between the direction vectors.)

How could we demonstrate this difference between vernal equinox and summer solstice at home? Well, I think Mendel just revealed it.

 

[Mendel]

How could we demonstrate this difference between vernal equinox and summer solstice at home? Well, I think Mendel just revealed it.

It looks to me like you were going somewhere else, though?