Comparing flat Earth and spherical Earth from a geometric point of view

[Pertti Niukkanen]

Next week, Monday, April 8, 2024, Americans will get to admire a total solar eclipse. The path of the eclipse starts in the South Pacific Ocean, passes through North America (Mexico, USA, Canada) and ends in the North Atlantic (Figure 1). In terms of time, this hike takes approx. 3h 17min (that is, during this time, the total phase of the eclipse can be seen somewhere on the globe). In Finland, however, we do not see even a partial eclipse.

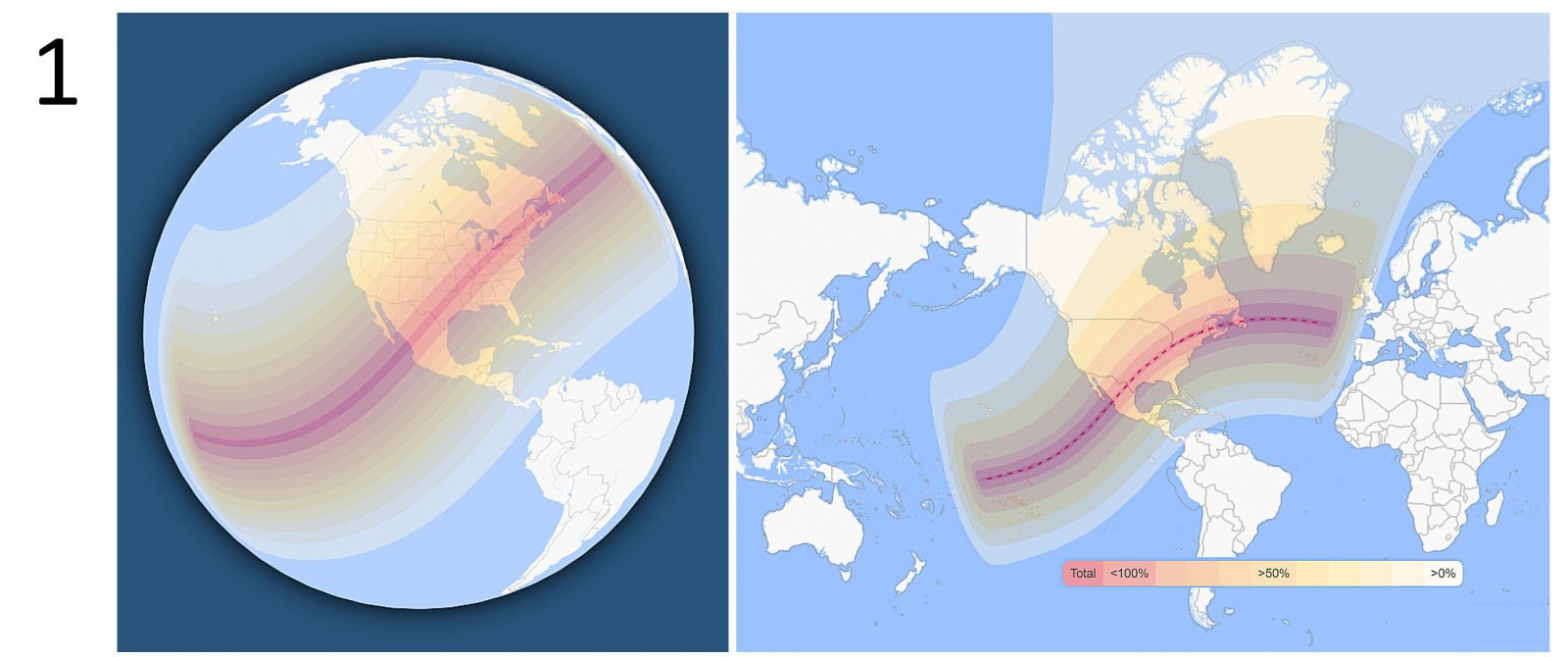
Figure 1 is from TimeAndDate's excellent eclipse site: https://www.timeanddate.com/eclipse/solar/2024-april-8. You should also look at the Wikipedia article https://en.wikipedia.org/wiki/Solar_eclipse_of_April_8,_2024 (e.g. the gif animation is illustrative).

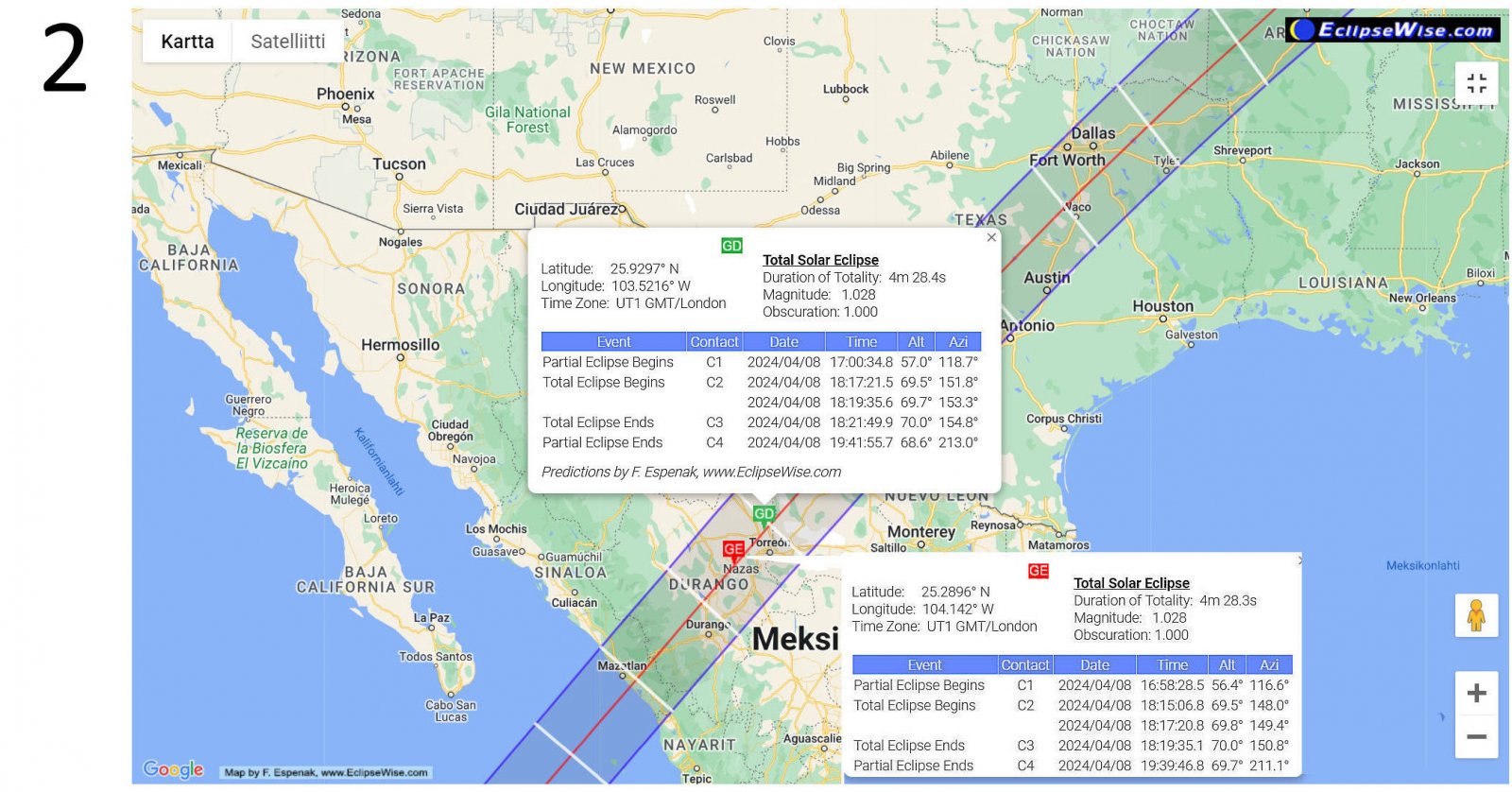
The site EclipseWise is also useful, https://www.eclipsewise.com/solar/SEgmapx/2001-2100/SE2024Apr08Tgmapx.html. By clicking on the map, you get a lot of additional information (Figure 2). Using this map, I picked 15 points along the path of the total eclipse:

Point –––– Coordinates
1 –––––– -7.8217, -158.5334 (eclipse begins)
2 –––––– -5.3651, -146.1835
3 –––––– -1.1486, -134.9775
4 –––––– 5.7957, -123.7143
5 –––––– 16.1349, -112.5082
6 –––––– 25.2896, -104.1420
7 –––––– 33.9292, -94.5346
8 –––––– 39.8081, -85.4379
9 –––––– 43.7389, -76.3852
10 ––––– 46.4412, -66.9677
11 ––––– 48.4069, -55.1025
12 ––––– 49.0771, -44.9379
13 ––––– 48.9654, -33.7758
14 ––––– 48.3010, -25.8657
15 ––––– 47.6189, -19.7857 (eclipse ends)

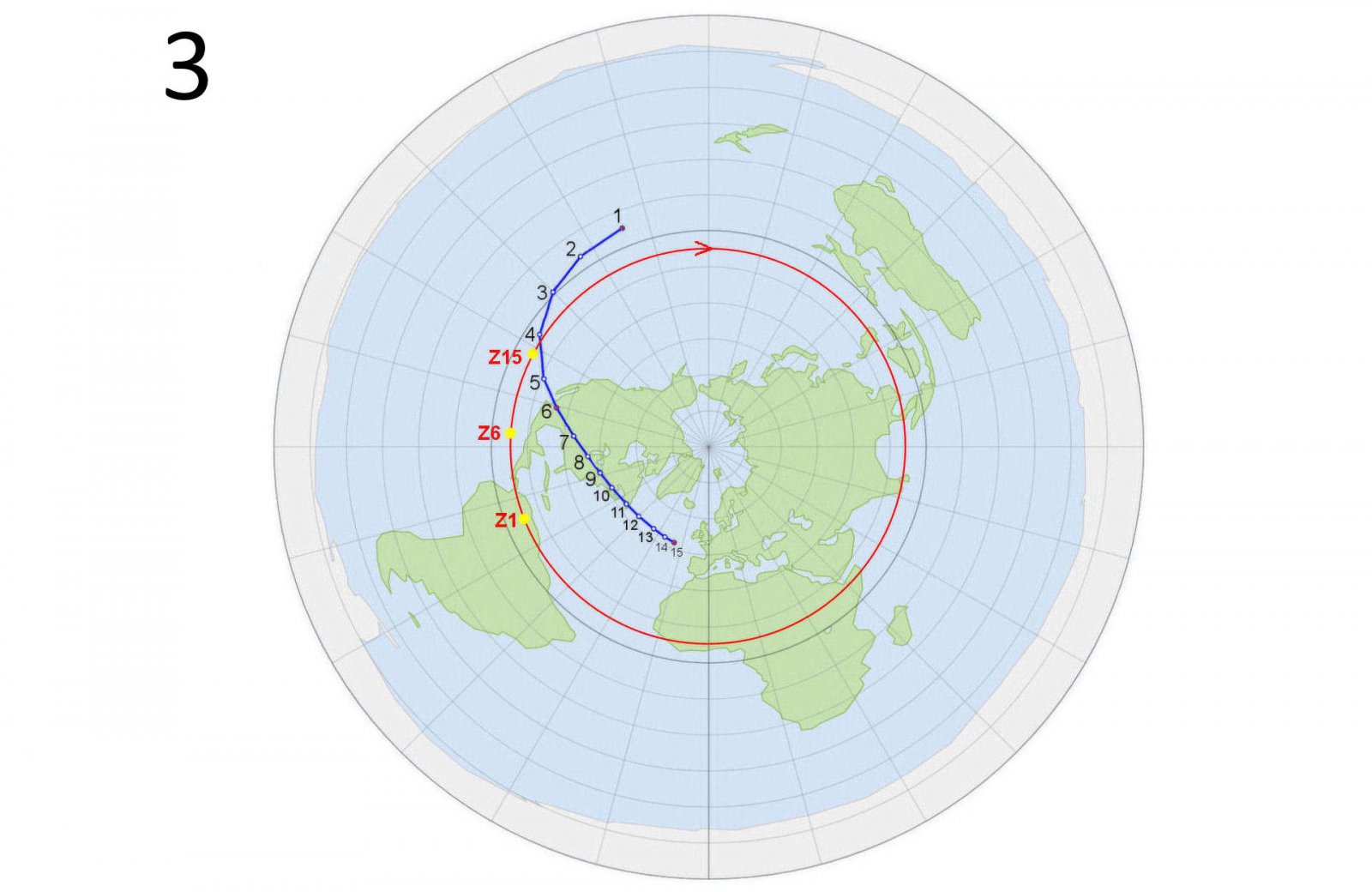
I placed the points on the FE map and got the path shown in Figure 3. At point 6 (Nazas, Durango, Mexico) the total phase takes the longest time (4min 28s according to Wikipedia). Such long totality requires that the angular diameter of the Moon is clearly larger than that of the Sun. I calculated that it is about 0.55 degrees for the Moon and about 0.53 degrees for the Sun.

In Figure 2 there is a red mark GE (GE = the point of Greatest Eclipse) at Nazas. This is the place where the eclipse is at its greatest (the width of the umbra is greatest). The green mark GD (GD = the point of Greatest Duration) is the place where the total phase lasts the longest time during the entire eclipse. GE and GD are usually close to each other (like this time too).

Flat Earthers might argue that it is not certain whether the Moon causes the solar eclipse. However, photos of the total phase show that the object covering the Sun is the Moon. The light reflected from the Earth (earthshine) illuminates the Moon to such an extent that the features of the Moon are visible in the image with a long exposure time (see the meme in Figure 4). More eclipse photos and videos: https://hdr-astrophotography.com/high-resolution-2019-total-solar-eclipse.

Figure 5 shows the situations at the beginning of the totality (Point 1), at the maximum phase (Point 6) and at the end of the totality (Point 15) using TimeAndDate's Day and Night World Map. The zenith points of the Sun and the Moon (Subsolar Point and Sublunar Point) have also been calculated in the picture. The Sun's zenith points are also marked in Figure 3 as points Z1, Z6 and Z15.

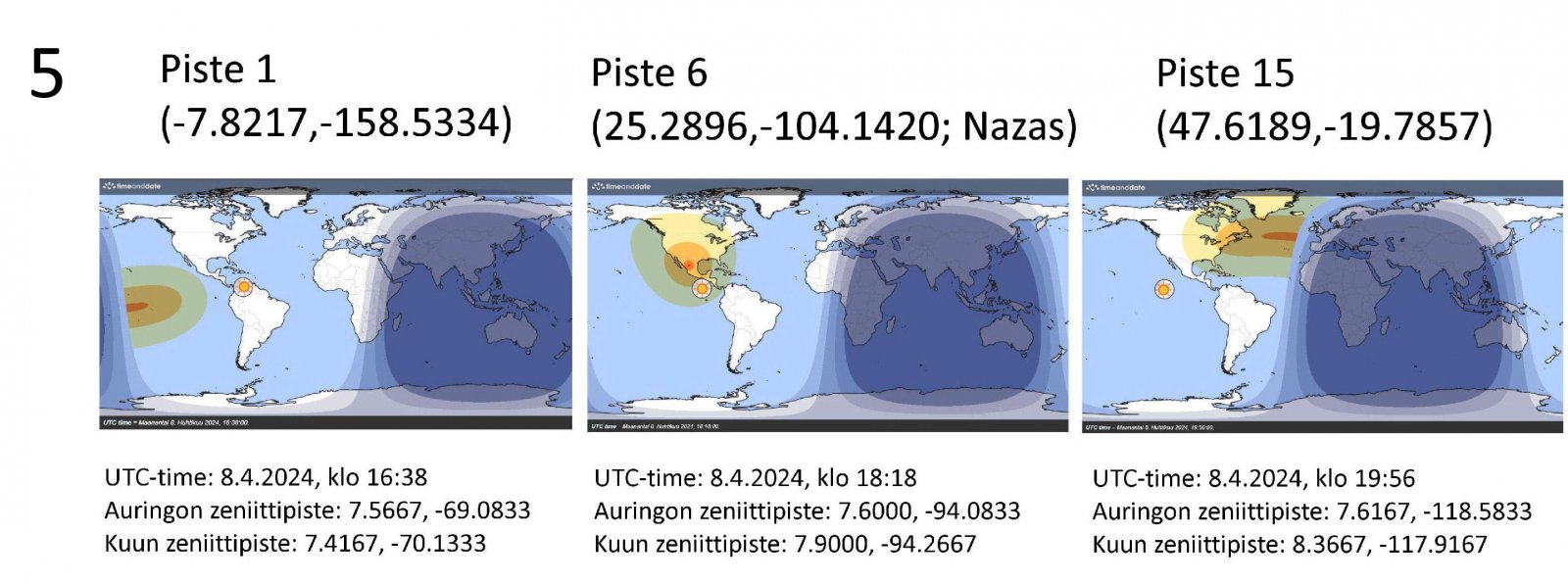
In image series 5, the zenith points of the Sun and the Moon appear to be almost on top of each other. However, they are not, as shown by the fact that the coordinates are not exactly the same. If they were exactly the same, a total solar eclipse would be seen exactly at the zenith. This event is theoretically possible, but certainly extremely rare in reality - has it ever happened?

We are quite close to the situation above at 18:18 UTC time. Then there is a total phase at Nazas (point 6) and at the same time there is a partial eclipse at the zenith point of the Sun (7.6000, -94.0833).

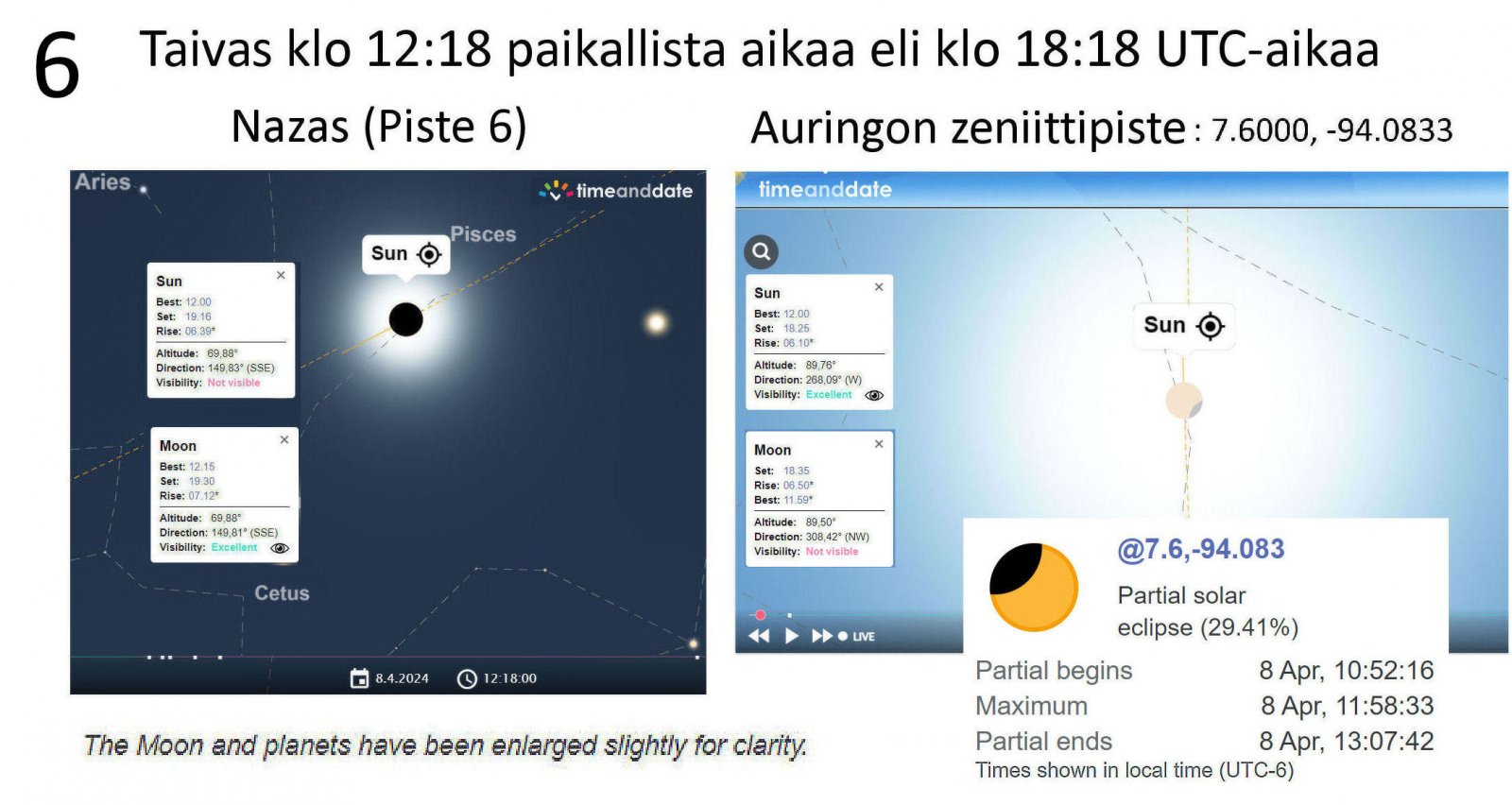
The situation is shown in Figure 6. In the picture on the right, I have cheated a bit. There the time is actually 18:19 UTC. So the Sun is no longer exactly at the zenith. However, its altitude is 89.76 degrees, so we are very close to the zenith. At the same time, the altitude of the Moon is 89.50 degrees, so it is also close to the zenith. (That extra minute made a little black slice to the disk of the Sun.)

The maximum partial eclipse at that location (7.6000, -94.0833) is at 17:58:33 UTC, when the coverage is about 29.4 percent. But then the altitude of the Sun is 85.17 degrees and the altitude of the Moon is 85.41 degrees. So they are not very close to the zenith.

Above, I have only told what astronomy predicts about next Monday's eclipse. At least the Americans can see how well the predictions come true. TimeAndDate also considers the accuracy of eclipse calculations, https://www.timeanddate.com/eclipse/accuracy.html. The article states that perfect accuracy is impossible. This is of course true. However, if the model is able to predict eclipses with an accuracy of one minute for centuries ahead, I think it can be considered correct and reliable.

What about the FE model? Let's look at Figure 3 again.

The events mentioned above (eclipse path, Sun's zenith points, etc.) can be placed on the AE map (the so-called flat Earth map). In Figure 3, the Sun's orbit is a red circle. When the Sun is above point Z1 at an altitude of 5000 km, a shadow is cast on point 1. When the Sun is above point Z6, a shadow is cast on point 6. And the zenith point Z15 casts the shadow on point 15.

In general, FE theory accepts that the shadow is produced by the Moon (at least I think so). The Moon, on the other hand, is assumed to be the same size as the Sun (diameter approx. 50 km). What should the Moon's orbit be like in order to get an eclipse path like in Figure 3?

If the Moon travelled the same path as the Sun (albeit at a different speed), a shadow would never form on the Earth's surface. In addition, they would collide with each other. So the Moon's orbit must be "below" the Sun's orbit. But how far? And is it even a circle with the North Star as its center?

If the Sun and the Moon are the same size (diameter approx. 50 km), the width of the umbra is also always 50 km, regardless of their mutual distance or the distance to the Earth. In reality, the width of the umbra varies between 0 km and 270 km at different eclipses. On Monday, the maximum width of the eclipse band is approx. 200 km.

So at least the FE model I described cannot predict the observations correctly. So what is the model that can do this? We look forward to this.

 

[JMartJr]

Nice post, @Pertti Niukkanen !

I had fun explaining to some folks earlier this week why the eclipse path movies from a westerly point towards the East, when the Sun and the moon cross the sky from East to West. Well, I had "fun."

Short answer is, the Sun and moon appear to rise and set, as you all know, because of the Earth turning, the surface of the Earth is going East at around 1,000 mph at the equator -- BUT the moon is actually moving East at over 2,000 miles per hour in its orbit. So the "anti-searchlight beam" of the shadow also sweeps West to East at about 1,000 mph at the equator (faster at the poles because round Earth, ground nearer the poles ain't headed East as quickly as ground at the equator...)

Video that explains in an accessible way, but in more detail and with less glossing details for the sake of not typing too long, is here:

Source: https://youtu.be/ujYYlXP12m4

 

[Pertti Niukkanen]

I had fun explaining to some folks earlier this week why the eclipse path movies from a westerly point towards the East, when the Sun and the moon cross the sky from East to West. Well, I had "fun."

Here's my old sketch of the solar eclipse. The situation is greatly simplified in the picture:
– Orbits are circles (actually slightly elliptical).
– The Moon's orbit around the Earth is in the same plane as the Earth's orbit around the Sun (actually at an angle of approx. 5 degrees).
– The Earth's axis is perpendicular to the orbital plane (actually at an angle of approx. 23.4 degrees).

In the picture, the orbital speed of the Moon is 3680 km/h. I don't remember where I got this value. If the value 2415000 km is used for the length of the Moon's orbit and the value 656 h for the orbital period (sidereal month = 27.32 d), we get approximately that orbital speed.

In my sketch, the situation is viewed from the north of the Earth (i.e. "from above"). In initial situation 1, observer P is on the equator in the Gulf of Guinea at point (0,0) and the shadow is formed at point V1.

After an hour (situation 2), the shadow hits point V2, but at the same time the Earth has rotated 15 degrees. The shadow has approached the observer, but has not yet reached him/her.

It should be noted that although the Moon's path is a circle, it can be considered a straight line here. Also the directions of the shadow from the Moon to the Earth are parallel, because the Sun is very far away.

After two hours (situation 3), the shadow of the Moon has already passed the observer P. I calculated that the observer would have seen the eclipse at time t = 1.89 h.

In a solar eclipse, the shadow travels from west to east. Flat Earthers think there is a contradiction here, because the Sun rises in the east, the Moon rises in the east and the stars also rise in the east. I hope the sketch shows that there is no contradiction.

 

[Pertti Niukkanen]

A total solar eclipse was seen in Nazas, Mexico (N = 25.2896, -104.1420) on 04/08/2024 at 18:18 UTC. At the same time, the Sun's zenith point was Z = 7.6000, -94.0833. Here are the points on the FE map.

We assume that the sun is approx. 5000 km high and approx. 50 km in diameter. The distance from point N to point Z is approx. 2428 km on the FE map, so we get the Sun's altitude at the time of the eclipse to be approx. 64.1°. We know that the Moon is somewhere along the NA, but where exactly?

The sketch on the right shows the situation (not to scale). The diagram assumes (as in most FE models) that the diameter of the Moon is the same as that of the Sun, approx. 50 km. In this case, regardless of the height of the moon, the width of the Umbra is always the same 50 km. The shadow is a circle only if the eclipse occurs exactly at the zenith (i.e. Z = N). Otherwise, the shadow is an ellipse with a minor axis of 50 km. In Nazas, the Sun's altitude is 64.1° at the moment of total eclipse (i.e. it is not at the zenith). From this we can calculate that the major axis of the resulting ellipse is approx. 55.6 km.

Nazas was the closest place to the Sun's zenith point during this eclipse. At other eclipse places, a much more eccentric ellipse would have been obtained. So in the FE model the shadows are not circles any more often than in the GE model. However, in the globe model, ovals are not ellipses (unless the eclipse happens exactly at the zenith, which hardly ever happened).

How high is the Moon according to the FE model? The size of the umbra is always 50 km wide regardless of the height of the Moon, so this does not solve the problem. On the other hand, the size of the penumbra depends on the height. If the Moon is very close to the Sun, a very large elliptical penumbra is obtained (dashed lines in the picture). The distance to the Moon could therefore be deduced by observing the size of the penumbra at the time of the eclipse. This as a tip for FE researchers.

In reality, the shape of the penumbra on Earth is anything but an ellipse. The width of the umbra path was also approx. 198 km in Nazas (not 50 km).

Another challenge for FE theorists is that the Sun's altitude was 69.88° at Nazas. It was not 64.1° as predicted by the FE model. But this is already a familiar situation. For "some reason" the Sun is never observed where it should be according to the FE model.

 

[Pertti Niukkanen]

I tried to calculate the distance to the Moon based on the Nazas eclipse data (assuming that the radius of the Earth is 6371 km).

Bislin's distance calculator (http://walter.bislins.ch/bloge/index.asp?page=Creating+Flight+Plans+for+Flat+Earth) gives the GE distance between Nazas ( N ) and the Moon's zenith point (Z) as 2198.943116 km (N = 25.2896, -104.1420 and Z = 7.9000, -94.2667). This gives the angle α = 19.775571°. In addition, TimeAndDate reports that the Moon's altitude was β = 69.88°.

With this information we can calculate the distance to the Moon. In my calculation, I got the distance to be 358194 km (see picture). The correct value is approx. 384400 km, so the result is of the same order of magnitude.

The calculation is very sensitive to the altitude value. For example, with the value β = 69.90°, we would get a distance of approx. 380300 km. There can be inaccuracies and small errors in other starting data too.

In any case, this experiment shows (at least on a qualitative level) that the "ball model" gives consistent results. Of course, this does not convince FE-people, because the calculation assumes the "R-value" 6371 km. Let this excuse be a consolation to them.

 

[Pertti Niukkanen]

Is it possible that the Sun and the Moon orbit at the same (or almost the same) height above the flat Earth?

In an ingeniously simple experiment, Aristarchus of Samos (310 – 230 BC) determined the ratio of the distances of the Sun and the Moon. (Here you don't need to know the magnitudes of the distances.)

The experiment requires that the Sun and the Moon are visible in the sky at the same time and that the Moon's phase is exactly first or last quarter.

The diagram represents Aristarchus' idea. At Half Moon time, the angle SME is 90°. By measuring the angle α between the Sun and the Moon, the ratio x/y of the distances of the Sun and the Moon can be calculated. It is given by the formula x/y = 1/cosα.

A couple of examples:
α (°) –––––– x/y
60 ––––––– 2.0
70 ––––––– 2.9
80 ––––––– 5.8
85 –––––– 11.5
87 –––––– 19.1
88 –––––– 28.7
89 –––––– 57.3
89.85 ––– 382.0

According to current knowledge, the average distance of the Sun is 149,597,870 km and the Moon 384,400 km. With these values, the ratio x/y is approx. 389.2. This roughly corresponds to an angle α = 89.853°.

Aristarchus got the angle α = 87° in his experiment. This gives roughly the ratio of the distances x/y = 20 (cf. the table above). The correct ratio is about 390, so the result does not look very accurate. In any case, it shows that the Sun is much further away than the Moon. So the FE hypothesis of Sun and Moon at the same height is wrong.

Although the test is simple in principle, it is not so in practice. It must be done during the day, when the Moon is not very clearly visible. The biggest source of error in Aristarchus' experiment is the determination of the exact moment of Half Moon. I calculated that the error of 3 hours causes an error of more than 2 degrees in the angle α. This, in turn, can cause an error of up to one order of magnitude in the ratio x/y.

As far as I know, Aristarchus' test was not repeated in ancient times (perhaps precisely because of its difficulty). His results were still valid almost 2000 years later, e.g. Tycho Brahe:

"The implicit false solar parallax of slightly under three degrees was used by astronomers up to and including Tycho Brahe, c. AD 1600. Aristarchus pointed out that the Moon and Sun have nearly equal apparent angular sizes, and therefore their diameters must be in proportion to their distances from Earth." https://en.wikipedia.org/wiki/Aristarchus_of_Samos.

 

[AmberRobot]

That experiment requires that the moon's light is reflected light from the sun off of a spherical object. Not all flat earthers (if any) seem to hold that opinion.

 

[Pertti Niukkanen]

How much does the direction of the Sun change in an hour? The story continues.

On equinoxes, the Sun is at the celestial equator (declination β = 0°). In this case, the change angle γ = 15°. At the summer solstice, the Sun is approx. 23.4° north of the equatorial plane (declination β = 23.4°) and at the winter solstice approx. 23.4° south of the equatorial plane (declination β = -23.4°). On both solstices, the change angle γ is approx. 13.76°.

In my old post (https://www.metabunk.org/threads/co...m-a-geometric-point-of-view.12591/post-313249) I presented an experiment to determine the angle γ . I made the test on March 28, 2024, and the measurement result was quite precisely 15°. Due to cloudy weather, the test could only be done on 28.3. i.e. 8 days after the vernal equinox. Then, according to the theory, the angle γ was γ = 14.98°, i.e. slightly smaller than 15°. Such a difference could not be observed within the limits of the measurement accuracy of the experiment.
----------

In Helsinki the long period of heat and cloudless skies was coming to an end at the beginning of June. To be sure, my friend Ilkka and I did the "midsummer test" already on June 5, 2024. In this case, according to the theory, the angle γ should be 13.84°. (On the summer solstice it should be 13.76°.)

The image above shows the setup of the experiments. This time I attached the threads to the top of the miniature flagpole with superglue (it wasn't easy). I marked the shadow of the tip every hour with a marker on the surface of the table. Then I attached the small nails at the marks and tightened the threads from them. The angle γ is now the angle between the wires.

We measured the angle between wires 1 and 2, wires 2 and 3, and wires 5 and 6 with a protractor. In all three cases, the angle was approx. 14°. According to theory, the angle should be 13.84°. So within the limits of the measurement accuracy, we got the result predicted by the theory.

It would be good to repeat the experiment again at the autumn equinox and winter solstice. However, I firmly believe that the measurements give the results according to the "ball model" even then.

 

[Pertti Niukkanen]

The paths drawn by the gnomon tip have been presented on several forums. Here's a good combo video:


Source: https://www.youtube.com/shorts/xVEAXHdzRb0

The image below is related to this video. The author of the video is John Krieger, whose other videos can also be warmly recommended.