Comparing flat Earth and spherical Earth from a geometric point of view

[Pertti Niukkanen]

The idea of AE projection (azimuthal equidistant projection) is that the distances measured from a certain center point are preserved. The "semi-official" FE map is an AE map North Pole as the center point. So on the FE map, the distances measured from the North Pole are the same as on the globe map. In general, all distances measured along meridians are correct on the FE map.

Hardly anything else is correct. The areas of the Northern and Southern Hemispheres are of course the same in reality, but on the FE map the area of the southern "semi puck" is three times the area of the northern one. The FE map magnifies all areas and all distances (except those measured along meridians). Here are some examples of these "stretch factors":

– Earth's surface area: 2.46
– Northern Hemisphere area: 1.23
– Southern Hemisphere area: 3.70
– Length of the Equator: 1.57
– Distance in east-west direction at latitude 60°: 1.04
– Distance in east-west direction at latitude -60°: 5.19
– Distance from Perth to Sydney: 2.52

In Finland the FE map does not have very large distortions. In Helsinki (latitude 60), the east-west distance is only approx. 4% too long, further north even less. Distortions increase in the southern hemisphere. The most dramatic is the situation at the South Pole, where one point stretches into a circle about 125,700 km long.

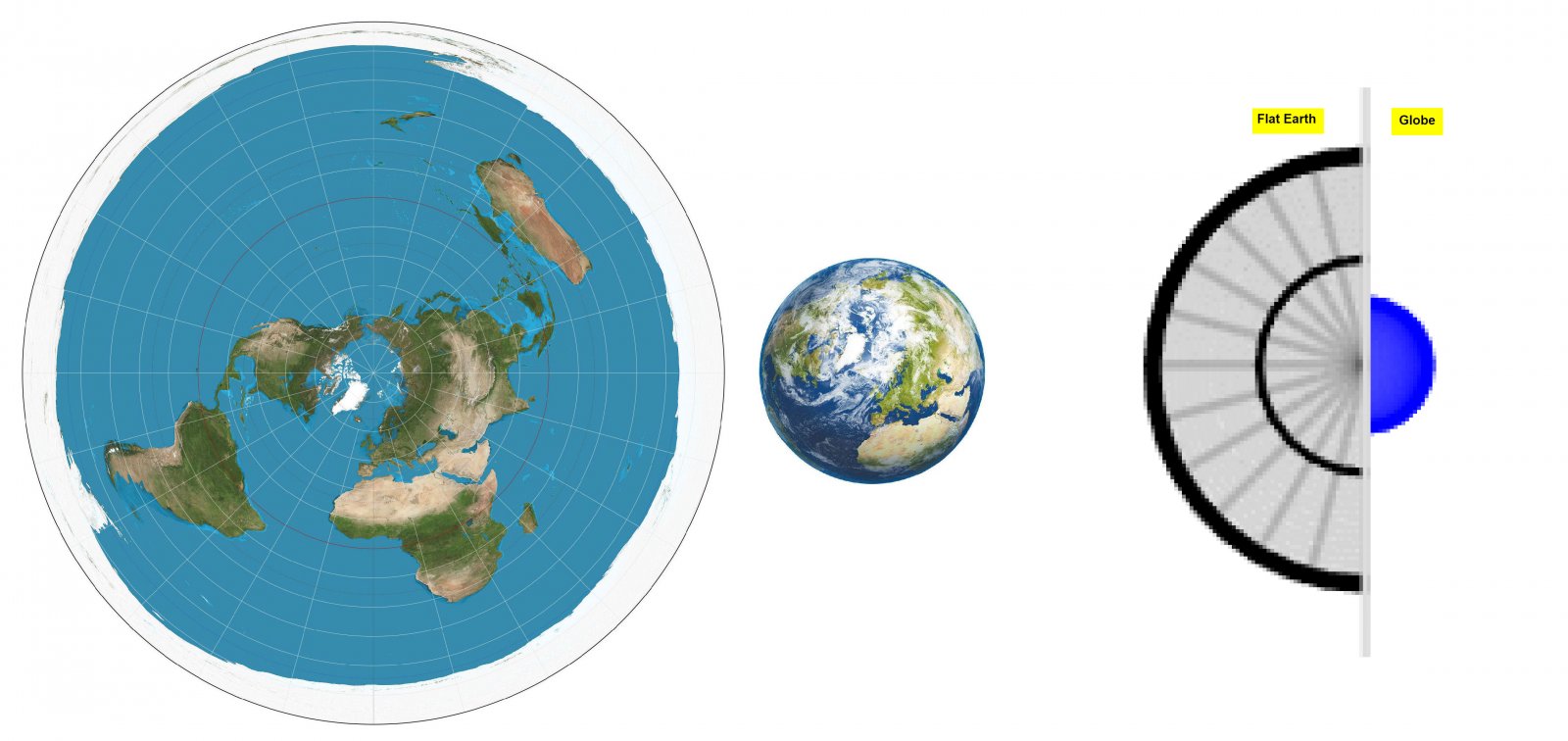
Below left are FE and GE to scale. The diameter of the FE disk is 40000 km, which is also the circumference of the Earth.

Below right is a magnified screen shot from Bislin's calculator. There are flat Earth and Globe side by side seen from a very long distance (70,000 km). http://walter.bislins.ch/bloge/inde...53-9-9-9-1~0.0343-10-10.00373383-1~86.204-9-4.

The ratio in these comparisons is about the same. So we can conclude that the radius of the flat Earth is 20000 km in Bislin's calculator too.

Another useful calculator made by Bislin is "Creating Flight Plans for Flat Earth", http://walter.bislins.ch/bloge/index.asp?page=Creating+Flight+Plans+for+Flat+Earth. It is easy to compare FE and GE distances by providing the coordinates of the locations. You get the coordinates e.g. from Google Maps by right-clicking on a place. Then click on the coordinates in the context menu and they will be copied to the clipboard in decimal format.

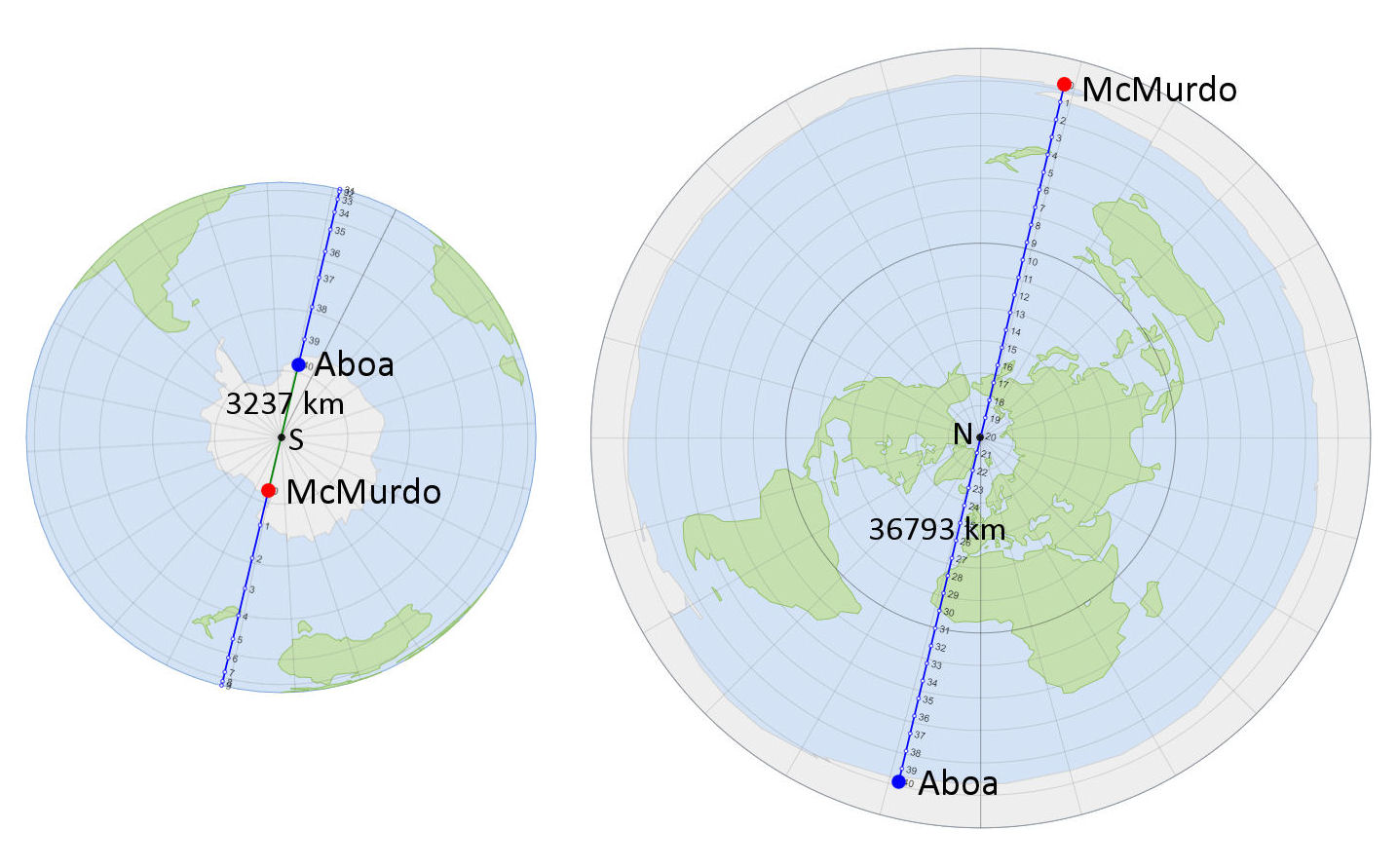
Most flat-earthers admit the existence of research stations located on the coast of Antarctica. Such are Finland's Aboa (-73.048,-13.420) and USA's McMurdo (-77.842,166.688). The direct route between these stations happens to go very precisely through the South Pole.

The image on the left shows the distance between these stations on the globe map (green segment). It is about 3240 km. That's roughly the distance between Detroit, Michigan and Sacramento, California.

On the right is the same journey on FE map. The shortest route between the stations goes through the North Pole. The length of the trip will be approx. 36,790 km.

Yes, the journey from Aboa to McMurdo could be made via the North Pole on the globe also. The length of this trip would also be 36,790 km. This is because the journeys are made along meridians, so both maps give the same values.

As a joint project between Aboa and McMurdo, a research flight from one station to another could be carried out. Leading figures of the FE community would also be included, agreeing to all their demands (research equipment, food, etc.) A stopover could be made at the South Pole in Amundsen Scott station. There could the researchers spend a night watching the midnight sun. (The station does have accommodation for tourists.)

Could this journey show to the flat-earthers which map was followed on the trip? Was the distance 3200 km or 37000 km? Perhaps something could also be deduced from the landscapes below.

If the budget of the research stations is not enough for this public education project, one could ask some of the world's many billionaires as a sponsor. They might be interested in the publicity value of the trip, especially if their own press people were going along. "Flat Earth supporters at the South Pole admiring Midnight Sun" sounds a very attractive tabloid headline.

=================

This post was originally in the thread "Measuring the Curvature of the Horizon with a Level", https://www.metabunk.org/threads/measuring-the-curvature-of-the-horizon-with-a-level.7832/page-4. There it was quite off-topic, and I had more like this in my mind. So I made a new thread with a broader title. Hope all FE debunkers find this thread.

 

[Pertti Niukkanen]

I made a kind of "Flat Earth Curve Calculator" with the Finnish version of Excel. In the English version, you have to make a couple of substitutions in the formulas:
PII() -> PI()
SQUARE ROOT -> SQRT
Note that in the Finnish version of Excel, the decimal separator is a comma.

The input data is:
R = the radius of the disk, put in the cell A2
h = the height of the observer above the center of the disk, put in the cell B2
α (deg) = the angle of view (horizontal FOV), put in the cell C2

As output data you get δ (deg), φ (deg), AC and s%. Let me explain.

δ (deg) is the most important result. It's called "Horizon Curve Angle" or "Left-Right Drop Angle". The derivation of angle δ is below. In Excel you must type the formula in the cell
D2:
=(ATAN(A2/B2)-ACOS(B2/(NELIÖJUURI((1-(SIN(C2*PII()/360))^2)*(A2^2+B2^2)))))*180/PII()

φ (deg) is "Horizon Dip Angle" (angle between eye level and the horizon). It's simply = 90° – β1. Type in cell
E2:
=90-ATAN(A2/B2)*180/PII()

AC is the distance of the horizon seen from point A. Type in cell
F2:
=NELIÖJUURI(A2^2+B2^2)

s% is a tricky one.
I don't know programming or computer graphics. Still, it would be fun to see a flat Earth horizon curve on the screen (like in Bislin's calculator). At a certain viewing angle, you see the horizon curve as an angular segment with a chord and a sagitta (bulge). Now the value s% tells how many percent of the chord the sagitta is on the screen.

These s% numbers are usually very small. For example, if Felix Baumgartner were 39 km above the FE North Pole, the number would be 0.026 (see the first image). So the sagitta is only 0.026 percent of the chord he sees at 60 degrees field of view. It's just a straight line.

If Felix could rise 4748 km height, he could see the curve at 90 degrees field of view like this:

The ratio s% = 5 gives three points. So I can fit an arc of a circle through these points. (There is only one such circle).

I'm not sure about my "graphical method". It hardly has much use. Fortunately, you can ignore it. Other values are not related to it. Also my formula might be wrong. Anyway, here it is. So type in the cell
G2:
=100/(2*TAN(C2*PII()/360)/TAN(D2*PII()/180))

----------------

So here is my Flat Earth Curve Calculator. I would be happy if someone tried it to see if it works.

Here, the observer is always at the center of the disc. So the situation is the same in every direction. Looking from some other place makes it harder. The Horizon Dip Angle will definitely vary depending on the place. How the angle δ varies, I have no idea.

 

[Mendel]

As a joint project between Aboa and McMurdo, a research flight from one station to another could be carried out.

Article:

2018 – Colin O'Brady (USA) completed an unsupported (no resupplies or supply drops) solo crossing of Antarctica (not including the ice shelves). He started inland at the end of the Ronne Ice Shelf on 3 November 2018, passed through the South Pole and arrived inland at the start of the Ross Ice Shelf on 26 December 2018.[52][53][54] Louis Rudd (UK), who started on the same day as Brady and took a similar route, completed his unsupported solo trek two days later, arriving at Ross Ice Shelf on 28 December 2018[55]

Source: https://en.m.wikipedia.org/wiki/List_of_Antarctic_expeditions

See also https://www.metabunk.org/threads/2022-antarctic-flight-74-gear.12395/ , Flat Earthers won't pay for such a flight.

 

[Pertti Niukkanen]

Above I said: "The Horizon Dip Angle will definitely vary depending on the place. How the angle δ varies, I have no idea." Well, now I have an idea or a hypothesis, but no proof for it.

From a point O at a height h above the center of the circular disk, the horizon is seen at a viewing angle α. This is just the situation where my "Flat Earth Curve Calculator" (FECC) can compute the Horizon Curve Angle δ. What if the viewing point moves to point A at the same height h? At the same viewing angle α, how the angle δ changes?

Below on the left is a view of the situation from above. The red α is equal to the black α, although it appears slightly larger when viewed from above. The side view shows the corresponding horizon curve angles δ1 and δ2.

My hypothesis now is that the angles δ1 and δ2 are equal. Despite my best efforts, I have not been able to prove this claim.

I was talking about this problem with my friend at a round table. So he took two photos with his cell phone, one at the middle of the table and the other near the edge at the same height. The "horizon curves" look very much the same (see below on the right). The "test arrangement" was not very accurate, I must say. However, it did not contradict my hypothesis.

So on the flat Earth, if you fly with an airplane from the North Pole to the South keeping the same height, the horizon curve angle δ also remains the same. In this respect the situation is the same as on the globe Earth.

However, the proximity of the edge can be noticed from the increasing "Horizon Dip Angle" φ. In this respect the situation differs from the globe Earth, where the horizon dip angle keeps the same. This is of course because the spherical Earth has no edge.

I think this result is quite surprising. Unfortunately, it remains unproven. Maybe someone knows if the hypothesis is right or wrong.

 

[Mendel]

My hypothesis now is that the angles δ1 and δ2 are equal. Despite my best efforts, I have not been able to prove this claim.

I think this result is quite surprising. Unfortunately, it remains unproven. Maybe someone knows if the hypothesis is right or wrong.

View attachment 53953

You can often find a shortcut to a disproof by considering a special case.

Let α=180⁰.
That makes one leg of δ be h.
Since h and the radius are orthogonal, δ is now part of a right triangle.
Since the right triangles involving A and O are not similar, the δ angles have to be different.

Your hypothesis is therefore not true in general.

 

[Pertti Niukkanen]

Let α=180⁰.
That makes one leg of δ be h.
Since h and the radius are orthogonal, δ is now part of a right triangle.
Since the right triangles involving A and O are not similar, the δ angles have to be different.

Your hypothesis is therefore not true in general.

To get one side of the angle δ2 perpendicular to the disk, the angle α seen from point O cannot equal 180° (see below). On the other hand, this "perpendicular condition" α = 2*arctan (R/h) can be fulfilled in many ways. For example: R=1, h=1 and α=90°.

The situation α = 180° is only possible if h=0. In this case, the angle δ=0, regardless of where the horizon is seen from. If this trivial solution is accepted, my hypothesis still stands.

 

[Pertti Niukkanen]

Just a little more thought.

To get one side of the angle δ2 perpendicular to the disk the condition α = 2*arctan (R/h) must prevail. This can be realized in many ways. These are special cases where the sides of the viewing angle α touch the disk just barely. The angular segment seen at the Horizon Curve Angle δ2 is half of the entire disk. (See three cases below.)

What if the viewing point moves now from point O to point A at the same height h? At the same viewing angle α the sides of α do not touch the disk at all. So there is no angular segment or Horizon Curve Angle δ1. In this case, my hypothesis is pointless.

Usually, the values of R, h and α are such that this problem does not occur (R large, h and α relatively small). If this hypothesis becomes a theorem, it will certainly require many restrictive conditions.

 

[JMartJr]

That certainly explains why flat Earth theorists never put a scale on their world maps. Kinda gives it away, don't it?

 

[Pertti Niukkanen]

I tested my hypothesis by calculating "backwards" some cases. The table below shows the results when the disc radius is 10 and the viewing angle is 60°. Horizon curve angle δ1 is the angle at a distance x from the center of the disk at a height h. Horizon curve angle δ2 is the value from my FECC calculator for reference. The last column shows the ratio δ1/δ2.

These tests show inevitable, that my hypothesis is not true. The differences compared to the value of the angle δ2 in the middle of the disk seem to be quite small, usually a couple of percent at most. The difference very close to the edge may be greater, but I was not able to test that situation.

So my hypothesis is wrong. It's still quite surprising how similar the curve is in my friend's photos. Visually, it is difficult to notice the difference even relatively close to the edge.

 

[Pertti Niukkanen]

With Bislin's calculator you can see the horizon curve in Globe model, in FE model and the two side by side. Below are the curves seen from height h = 1500 km at the viewing angle α = 60° (Note: to get horizon FOV 60° you must type in View∠ -box the value 1.20185*60 = 72.111. This is the diagonal FOV that the calculator expects to have.)

In all three cases the values like horizon distance, horizon dip angle or horizon curve angle are given only for the Globe model. So I cannot compare these values directly with my FECC calculator. I can only compare the graphic images of the horizon. http://walter.bislins.ch/bloge/inde...1-9-9-7~0.0343-10-10.00373383-1~86.204-9-31-1

There is also the Grid option "Projected". Bislin explains:

"For comparison with the Flat-Earth model, a red grid can be displayed with the Grid setting Projected. The red grid shows the projection of the blue grid onto the plane of the Flat-Earth. For low altitudes, the deviations between the blue ball grid and the red flat grid are minimal. So small indeed that by turning off the red grid the curvature can barely be noticed."

So the red "grid curve" is not the curve of the FE horizon. It's the curve of a disk with radius HorDistX d = 3741.18 km at the same height 1500 km.

To get comparable graphs of the GE and FE curves in Bislin's calculator, I adjusted the Tilt value so that the red line segment between the two small triangles fills the entire width of the graph window. From the corresponding FE graph I can now measure the curve which should be comparable with FECC calculator's value.

FECC calculator gives s% = 1.01. So the sagitta of the curve is about 1 % from the chord. This is pretty much exactly the same ratio as measured from Bislin's graph. Maybe FECC "graphical method" works after all?

If the height h is very big, you will not get help from the GE graph. So I just adjust the Tilt value at maximum 45°. Then I measure the ratio of sagitta and chord. http://walter.bislins.ch/bloge/inde...9-9-9-1~0.0343-10-10.00373383-1~86.204-9-31-1

In the example below I measured on the screen the chord = 35.2 cm and the sagitta = 2.4 cm. The ratio is 2.4/35.2 = 0.0682 = 6.82 %. FECC calculator gives s% = 6.855. Taking measurement accuracy into account this fits also pretty well. The Tilt affects a little on the graph of the horizon curve. Why I chose the maximum Tilt value 45°, I have no argument.

So to see the FE horizon curve precisely is quite a complex task in Bislin's calculator. The FECC calculator gives some precise numbers and an elementary way to draw the graph too. It could be fun if somebody with programming skills made it as a little app.

On the other hand, who cares. On the spherical Earth the horizon is real and it's interesting to see how the calculator imitates this reality. The FE model has no reality to compare the FE calculator to. Because the Earth is not flat.

 

[Pertti Niukkanen]

Back to the Globe.

Knowing the viewer height is enough to calculate the distance and the dip angle of the horizon. In order to calculate the target's hidden height, the distance of the target must also be known. This hidden height is probably the most important piece of information when evaluating FE photos.

Yet FE people are more (or solely) interested in the "drop" caused by the curvature of the Earth. Drop is the amount the curve of the earth drops away from level. It can be calculated in various ways, all of which are roughly the same for distances under 100 miles. The most commonly used is the drop perpendicular to level line.

The drop is the same as the hidden height when the viewer height is zero. Hardly anyone makes observations with their eyes on the ground, so I can't really find much use for this drop in image analysis or elsewhere.

However, the flat-earthers are very fond of this drop. As my FE friend asked me: "Do you really believe that I went 70 m downhill coming from Kerava to Helsinki?" Mostly they calculate the drop using the "8 inches per mile squared" rule. This is quite accurate at distances under 100 miles. It is much worse if this drop is considered a hidden height regardless of the viewer height.

The calculation of the drop is a fairly simple geometric task (see below).

The first formula is simpler. However, flat-earthers prefer the latter for some reason, even though it has trigonometric functions. Of course, both formulas give the same results.

The table shows the drop b values when R = 6371 km (= 3958.756 miles). The distance d is in kilometers or miles. The values of drop b are in the corresponding columns.

d (km/miles) ––– b (km) –––––––––––– b (miles)
1 –––––––––– 0.000078481 –––––––––– 0.000126302
2 –––––––––– 0.000313922 –––––––––– 0.000505209
3 –––––––––– 0.000706326 –––––––––– 0.001136721
4 –––––––––– 0.001255690 –––––––––– 0.002020837
5 –––––––––– 0.001962016 –––––––––– 0.003157559
6 –––––––––– 0.002825303 –––––––––– 0.004546886
7 –––––––––– 0.003845551 –––––––––– 0.006188818
8 –––––––––– 0.005022761 –––––––––– 0.008083356
9 –––––––––– 0.006356933 –––––––––– 0.010230500
10 ––––––––– 0.007848066 –––––––––– 0.012630251
20 ––––––––– 0.031392323 –––––––––– 0.050521245
30 ––––––––– 0.070632945 –––––––––– 0.113673709
40 ––––––––– 0.125570222 –––––––––– 0.202088850
50 ––––––––– 0.196204559 –––––––––– 0.315768362
60 ––––––––– 0.282536480 –––––––––– 0.454714421
70 ––––––––– 0.384566622 –––––––––– 0.618929689
80 ––––––––– 0.502295739 –––––––––– 0.808417310
90 ––––––––– 0.635724701 –––––––––– 1.023180915
100 –––––––– 0.784854497 –––––––––– 1.263224618
200 –––––––– 3.139998398 –––––––––– 5.055320108
300 –––––––– 7.067175087 ––––––––– 11.383574642
400 ––––––– 12.569297382 ––––––––– 20.260213269
500 ––––––– 19.650458367 ––––––––– 31.702516913
1000 –––––– 78.970041394 –––––––– 128.384081627
2000 ––––– 322.062820627 –––––––– 542.361859696
3000 ––––– 750.533738203 ––––––– 1375.783158849
3958 –––– 1378.618103550 ––––––– 3881.399517828
4000 –––– 1412.205690896
5000 –––– 2422.628057034
6000 –––– 4228.655256500
6371 –––– 6371.000000000

A quote from FlatEarth.ws site, https://flatearth.ws/curvature-calculation

>>
The most common error is not taking the observer's height into account. They would only calculate drop from the horizontal plane. It doesn't matter if they are using engineering grade AutoCAD 2016 with 15 digit precision, the numbers will be incorrect if the geometry is wrong in the first place.
– – –
'Using AutoCAD 2016 with 15-Digit Precision'™
The following is the legendary Earth's curvature chart made by a flat-Earther "using AutoCAD 2016 with 15-Digit precision"™. While technically not entirely inaccurate, the chart is often abused by flat-Earthers to calculate the expected amount of obstruction when it is unsuitable for such purpose, and actually is not that much useful anywhere else.
>>

You can see this "legendary Earth's curvature chart" above left. The values "By Geometric" are of course the same as "By Trig". The radius of the Earth is now R = 6373 km. So I made the drop calculations for this radius also:

d (km/miles) ––––– b (km) ––––––––––– b (miles)
1 ––––––––––– 0.000078456 ––––––––– 0.000126263
2 ––––––––––– 0.000313824 ––––––––– 0.000505051
3 ––––––––––– 0.000706104 ––––––––– 0.001136364
4 ––––––––––– 0.001255296 ––––––––– 0.002020203
5 ––––––––––– 0.001961400 ––––––––– 0.003156568
6 ––––––––––– 0.002824416 ––––––––– 0.004545459
7 ––––––––––– 0.003844344 ––––––––– 0.006186876
8 ––––––––––– 0.005021185 ––––––––– 0.008080819
9 ––––––––––– 0.006354938 ––––––––– 0.010227290
10 –––––––––– 0.007845603 ––––––––– 0.012626287
20 –––––––––– 0.031382472 ––––––––– 0.050505390
30 –––––––––– 0.070610779 ––––––––– 0.113638034
40 –––––––––– 0.125530814 ––––––––– 0.202025426
50 –––––––––– 0.196142984 ––––––––– 0.315669258
60 –––––––––– 0.282447809 ––––––––– 0.454571705
70 –––––––––– 0.384445928 ––––––––– 0.618735424
80 –––––––––– 0.502138094 ––––––––– 0.808163558
90 –––––––––– 0.635525176 ––––––––– 1.022859734
100 ––––––––– 0.784608160 ––––––––– 1.262828062
200 ––––––––– 3.139012506 ––––––––– 5.053731600
300 ––––––––– 7.064954777 –––––––– 11.379991906
400 –––––––– 12.565345041 –––––––– 20.253822437
500 –––––––– 19.644272512 –––––––– 31.692487626
1000 ––––––– 78.944947810 ––––––– 128.342441876
2000 –––––– 321.956371005 ––––––– 542.164648384
3000 –––––– 750.266767843 –––––– 1375.121633033
3959 ––––– 1378.858632357 –––––– 3871.071804633
4000 ––––– 1411.636376962
5000 ––––– 2421.401715761
6000 ––––– 4224.714869949
6373 ––––– 6373.000000000

Comparing these values with the AutoCAD 2016 values we find quite large differences at distances 1–9 km. After that, the values are exactly the same. Of course I'm relying on my own numbers and assuming that FE engineer Brian Mullin & co have miscalculated.

Above right is the Imperial version of the same legendary map. It's from a tweet from the Flat Earth Society,
Source: https://twitter.com/flatearthorg/status/936226165588725761

There, the radius of the earth is 3959 miles (= 6371.393 km). That's pretty close to 6371 km, so we can compare those numbers. Now it looks like the numbers are correct. Same team and same day, but the metric system is harder?

 

[Rory]

Yet FE people are more (or solely) interested in the "drop" caused by the curvature of the Earth.

Are you sure that's current? By referencing Brian Mullin and a FE Society tweet from 2017 I'm wondering how up to date you are.

I was into flat earth debunking from 2016-2019. I made quite a few calculators for various things, as lots of other people did (maybe I should put them all on a Google Sheet and share them).

I guess I felt that that battle had already been fought: the debunkers had done all the math and explained everything and the flat earthers had moved on to other arguments.

Have you reviewed all the literature that's already out there?

 

[Pertti Niukkanen]

Are you sure that's current? By referencing Brian Mullin and a FE Society tweet from 2017 I'm wondering how up to date you are.

Have you reviewed all the literature that's already out there?

Of course, that was an exaggerated statement. I myself know flat-earthers who calculate hidden heights and the effects of refraction in their photos.

Still, in my experience, the majority just recycle the arguments that were already known in Rowbotham's time. This summer I participated in the Official Flat Earth & Globe Discussion fb group for about a month. (https://www.facebook.com/groups/FlatEarthGlobeDiscussion). It was quite frustrating. The same material was moving there as years ago. I didn't notice any new claims or arguments.

In a sense, the battle was already fought from the start. The math to prove the Globe has been available for decades or centuries to those willing to see.

So what is left to debunkers? Make more pedagogical calculators, etc., hoping that this might change the minds of true believers? This is probably wishful thinking, but some on the edge of the rabbit hole may benefit from these efforts.

So it would be great if you can share those calculators. Of course I'm not up to date. I'm really interested, what literature do you mean? Can you name some?

 

[Pertti Niukkanen]

If you just want to know the geometric drop, there are many online calculators to tell you that. I think the best (also in this respect) is Metabunk's "Earth's Curve Horizon, Bulge, Drop, and Hidden Calculator". For example, if you give "Distance in Kilometers: 40" you instantly get "Geometric Drop = 125.57 meters". (https://www.metabunk.org/curve/?d=40&h=10&r=6371&u=m&a=a&fd=60&fp=3264)

"Earth Curve Calculator" by dizzib is useful also in calculating hidden heights (but only geometrically). To get the drop b you must put "h0 = Eye height": 0 metres. At "d0 = Target distance ": 40 km you get then "h1 = Target hidden height": 125.5677 metres. (https://dizzib.github.io/earth/curve-calc/?d0=40&h0=0&unit=metric).

The Omni Calculator "Earth Curvature Calculator", https://www.omnicalculator.com/physics/earth-curvature, also works this way. To get drop b you should put "Eyesight level": 0 m, but the calculator says "View level must be greater than 0". Fortunately, it accepts the value 0.000000001 m (1 nanometre), which is sure to give the correct drop: Obscured object part 125.567 m.

Walter Bislin's calculator "Finding the curvature of the Earth" is excellent in many ways (http://walter.bislins.ch/bloge/index.asp?page=Finding+the+curvature+of+the+Earth). However, finding the drop at a certain distance is not easy. The calculator gives the drop only at the distance of the horizon. It is marked somewhat cryptically with "DipHeight b". Unlike the Metabunk calculator, you cannot simply ask: What is the drop at 40 km.

Just to calculate the drop there is for example "Earth Curvature Calculator", https://earthcurvature.com. "Accurately calculate the curvature you are supposed to see on the ball Earth". From this introduction one could conclude that this calculator is made by a flat-earther for the flat-earthers. It does give the drop correctly though.

 

[Rory]

it would be great if you can share those calculators.

I'll have a look in my collection and see if I can put them all in Google Sheets (easier to share and update and manage).

If you're itching, though, most of them should probably show up in this search:

https://www.metabunk.org/search/537140/?q=spreadsheet+attached&c[users]=Rory&o=relevance

Not up to your level of math but some of them did some interesting things that hadn't been done at the time - as far as I'm aware - such as the one that predicts where mountain peaks and buildings will appear in photographs for either flat/sphere earth models and the obstruction calculator.

I'm really interested, what literature do you mean?

Sorry, that was a clumsy sentence that I can't really defend/define since there isn't really a collection of 'flat earth literature' that I know of, it just seems to have been something accumulated by those who were there at the time (I forget it's still a thing).

I wonder who has the best collection of stuff? Maybe https://flatearth.ws or https://mctoon.net. And pretty much everything is here on metabunk - but perhaps not so easy to find without a real trawl through the forum.

I'm sure a lot has changed since I last took a look.

 

[Mendel]

However, the flat-earthers are very fond of this drop. As my FE friend asked me: "Do you really believe that I went 70 m downhill coming from Kerava to Helsinki?"

That's an example of mixing FE thinking with globe analysis. It'd only "downhill" if you think "same level" is flat, when it's (very slightly) curved (as is the ocean) on the globe.

If you put a globe in flat-Earth-land (as FEers would do by placing a household globe on their kitchen table), you'd go "downhill", but on the globe, we don't. It can't be downhill both ways!

 

[Pertti Niukkanen]

This is a fairly recent (12/17/2021) video by flat-earther RV Truth: "The Lake Pontchartrain Bridge Proves Flat Earth". His "proof" is based solely on the drop. He says there should be a drop at the other end of the bridge as big as the Statue of Liberty with its pedestals.


Source: https://www.youtube.com/watch?v=CQfxtSvk23E

I use the numbers provided by the video (they are fairly correct when refraction is not taken into account). The length of the Lake Pontchartrain Causeway is 38.6 km. In the diagram, the arch AB (red) represents the Causeway Bridge. The length of the bridge is so small compared to the radius of the Earth that the arch AB, chord AB and tangent line segment AC (green) can be considered the same length. The geometric drop b is 117 m (116.93 m).

There is one more quantity called sagitta (or bulge), marked in the diagram with the letter s. It is the height of the circular segment, which concretely forms a visual barrier when looking at distant objects. In this case the sagitta is about 29 m (29.23 m). Is this what flat-earthers call "water mountain"?

The question about the drop of the bridge includes idea that the bridge should be built in the direction of the tangent, geometrically as a straight line (line segment AC). Of course, this is not the case, but the bridge follows the curved shape of the lake and is therefore approximately the same distance from the water surface the entire way (curve AB).

The models of the bridges are from Walter Bislin's "Soundy" simulation, about here: http://walter.bislins.ch/bloge/inde...0-10.1375-3~0.0343-10-11008.3105-114.7322-9-4

The picture on the left shows the Causeway Bridge (Bridge AB) seen from a height of 50 m. In this case, the distance to the horizon is approx. 25.2 km. Thus, the end of the bridge remains behind the horizon.

Let's imagine that a new similar bridge is built next to it, straight in the direction of the tangent (bridge AC). That would also be 38.6 km long. The distance of the end of the bridge from the ground would now be the drop calculated above = approx. 117 m. Therefore, 117 m high pillars would be needed to support the end. They really would be higher than the Statue of Liberty when erected next to it, whose height including the pedestals is approx. 92 m.

In addition, it can be calculated that the hidden height of the pillars (and the Statue of Liberty) when viewed from height 50 m is approx. 14 m. So this much of them remains hidden behind the horizon (dashed line).

Note that the pictures are "zoomed" to the end of the bridges, which emphasizes the differences. Hopefully, they give an idea of the drop that flat-earthers wish to see.

If you walk on bridge AB, you are walking on "level ground". Your spirit level is balanced. If you put a ball on the ground, it will stay there.

If you walk across bridge AC from A to C, you actually go "uphill", because the distance from the center of the Earth increases. The further you go, the greater the deviation of the spirit level. A ball placed on the ground rolls downhill towards A (if there is no friction).

The chord AB would represent an underwater tunnel in Lake Pontchartrain. There the ball would roll and stop in the middle of the tunnel regardless its original place (no friction).

 

[Mendel]

This is a fairly recent (12/17/2021) video by flat-earther RV Truth: "The Lake Pontchartrain Bridge Proves Flat Earth". His "proof" is based solely on the drop.

Does he explain why the bridge appears to curve down in Soundly's videos and photographs?

 

[Pertti Niukkanen]

Does he explain why the bridge appears to curve down in Soundly's videos and photographs?

The calculated childishness of the video suggests that it is only meant to keep his ignorant fans happy. If he knows about Soundly's videos or photos, he won't say. If forced to comment, the answer would probably be that they are fake – or some nonsense about refraction, perspective, vanishing point etc.

As childish these videos are, they can be quite suggestive and tempting. An ignorant layman trembling on the brink of the rabbit hole needs some antidote. In this case Soundly's videos and photos are just it.

Soundly's video "Here Is The Curve!" is a thorough discussion with surveyor Jesse Kozlowski. It is highly recommended, yet quite technical for the layman. Easier to adopt/adapt, yet eye-opening is the video "Lake Pontchartrain Causeway Time-lapse"


Source: https://www.youtube.com/watch?v=ybkgOD_4CTg

 

[Nada Truther]

This is a fairly recent (12/17/2021) video by flat-earther RV Truth: "The Lake Pontchartrain Bridge Proves Flat Earth". His "proof" is based solely on the drop. He says there should be a drop at the other end of the bridge as big as the Statue of Liberty with its pedestals.


Source: https://www.youtube.com/watch?v=CQfxtSvk23E

I use the numbers provided by the video (they are fairly correct when refraction is not taken into account). The length of the Lake Pontchartrain Causeway is 38.6 km. In the diagram, the arch AB (red) represents the Causeway Bridge. The length of the bridge is so small compared to the radius of the Earth that the arch AB, chord AB and tangent line segment AC (green) can be considered the same length. The geometric drop b is 117 m (116.93 m).
View attachment 54356
There is one more quantity called sagitta (or bulge), marked in the diagram with the letter s. It is the height of the circular segment, which concretely forms a visual barrier when looking at distant objects. In this case the sagitta is about 29 m (29.23 m). Is this what flat-earthers call "water mountain"?

The question about the drop of the bridge includes idea that the bridge should be built in the direction of the tangent, geometrically as a straight line (line segment AC). Of course, this is not the case, but the bridge follows the curved shape of the lake and is therefore approximately the same distance from the water surface the entire way (curve AB).

The models of the bridges are from Walter Bislin's "Soundy" simulation, about here: http://walter.bislins.ch/bloge/inde...0-10.1375-3~0.0343-10-11008.3105-114.7322-9-4

The picture on the left shows the Causeway Bridge (Bridge AB) seen from a height of 50 m. In this case, the distance to the horizon is approx. 25.2 km. Thus, the end of the bridge remains behind the horizon.

Let's imagine that a new similar bridge is built next to it, straight in the direction of the tangent (bridge AC). That would also be 38.6 km long. The distance of the end of the bridge from the ground would now be the drop calculated above = approx. 117 m. Therefore, 117 m high pillars would be needed to support the end. They really would be higher than the Statue of Liberty when erected next to it, whose height including the pedestals is approx. 92 m.

In addition, it can be calculated that the hidden height of the pillars (and the Statue of Liberty) when viewed from height 50 m is approx. 14 m. So this much of them remains hidden behind the horizon (dashed line).

Note that the pictures are "zoomed" to the end of the bridges, which emphasizes the differences. Hopefully, they give an idea of the drop that flat-earthers wish to see.View attachment 54357

If you walk on bridge AB, you are walking on "level ground". Your spirit level is balanced. If you put a ball on the ground, it will stay there.

If you walk across bridge AC from A to C, you actually go "uphill", because the distance from the center of the Earth increases. The further you go, the greater the deviation of the spirit level. A ball placed on the ground rolls downhill towards A (if there is no friction).

The chord AB would represent an underwater tunnel in Lake Pontchartrain. There the ball would roll and stop in the middle of the tunnel regardless its original place (no friction).

I would love to see the size of the elevators that raise the buildings up above the waterline as you approach the end of the bridge. (At about 5:15 in the video) They aren't there and then they slowly ascend as you move closer. That must be a huge engineering feat in itself!! And those people who are at the end of the bridge when the buildings start rising for me are probably like, "Hey, where are those buildings that are usually right here!?"

Fascinating!!

AND I would think that engineers that would look at you like a deer in headlights at the question of "did you put the curvature of the earth into consideration, when building this bridge?" (4:45), would look at you like that because they have never heard that silly of a question asked.

 

[Mendel]

I would love to see the size of the elevators that raise the buildings up above the waterline as you approach the end of the bridge.

Well, that these elevators don't exist is proof that Earth is flat, of course!

Article:

When I worked for Target Corp, we had a huge warehouse in CA.
When it was originally built, it followed the curve, to save excavation costs.
Years later, we added a large automated storage retrival system which had to be flat.
One end of the ASRS was level with the rest of the building, and the other end had steps.
It took some getting used to, as you didn't feel like you were going downhill in either situation.

Source: https://www.reddit.com/r/askscience/comments/avckgw/comment/ehgu2mm/

From the same thread:

If you are building something level, you have accomplished your goal if you can put a bubble level at any point on the surface and it shows it to be perfectly level. A level surface follows the curvature of the earth
If you are building a flat surface, you have succeeded if you can project a laser line from one inch off the surface of one end to one inch off the surface of another end and the laser is one inch off the surface at all points in between. A flat surface does not follow the curvature of the earth and will get further away from the surface of the earth the farther you go away from the center.

As we know, that's not entirely true as even the laser gets bent in the atmosphere, but if all you want is to see the other side, it's good enough.

If you're sending the laser in a vacuum, you need to be more precise. LIGO detectors use laser interferometry to measure the distortions in space-time occurring between stationary, hanging masses (mirrors) caused by passing gravitational waves.

Article:

Curvature of the Earth: LIGO's arms are long enough that the curvature of the Earth was a factor in their construction. Over the 4 km length of each arm, the Earth curves away by nearly a meter! Precision concrete pouring of the path upon which the beam-tube is installed was required to counteract this curvature.

Source: https://www.ligo.caltech.edu/page/facts

I've read a more detailed article on this, but I can't find it right now.

 

[Pertti Niukkanen]

The drop b at the distance d is derived in the sketch 1 (the formula in black frames). Actually b is the same as the sagitta when the chord c = 2d. So we get the sagitta s as a function of the chord c (sketch 2, the formula in red frames).

chord c ––––––– sagitta s
50 m ––––––––– 0.005 cm
100 m –––––––– 0.020 cm
1 km ––––––––– 1.962 cm
2 km ––––––––– 7.848 cm
3 km –––––––– 17.66 cm
4 km –––––––– 31.39 cm
5 km –––––––– 49.05 cm
6 km –––––––– 70.63 cm
7 km –––––––– 96.14 cm
8 km ––––––– 125.57 cm
9 km ––––––– 158.92 cm
10 km –––––– 196.20 cm
20 km –––––––– 7.85 m
30 km ––––––– 17.66 m
40 km ––––––– 31.39 m
50 km ––––––– 49.05 m
60 km ––––––– 70.63 m
70 km ––––––– 96.14 m
80 km –––––– 125.57 m
90 km –––––– 158.93 m
100 km ––––– 196.20 m
200 km ––––– 784.85 m
300 km ––––––– 1.766 km
400 km ––––––– 3.140 km
500 km ––––––– 4.907 km
600 km ––––––– 7.067 km
700 km ––––––– 9.621 km
800 km –––––– 12.569 km
900 km –––––– 15.912 km
1000 km ––––– 19.650 km

Flat-earthers love to say: Show me the curve! That hardly succeeds in the kitchen or backyard. In the long course swimming pool (50 m) the bulge (sagitta) is about 0.05 mm (= 50 micrometers). How do you measure it?

Even at 1 km is the sagitta only about 2 cm. At 10 km it's about 2 m, which is certainly large enough to see without a dipstick. On Lake Pontchartrain (38.6 km) the sagitta is 29.23 m.

Geodetic surveyor Jesse Kozlowski describes Lake Pontchartrain Causeway as "a man-made concrete structure monumenting the curvature of the earth". This is very aptly said. But how could we use this monument to show FE people the curve clearly and without math?
--------------------

Soundly's video "Here Is The Curve!" is a thorough discussion with Jesse Kozlowski. It is highly recommended. Also the comment section is interesting.


Source: https://www.youtube.com/watch?v=EIOs-PzNIZU


The same discussion is also on Jesse Kozlowski's YouTube channel under the same name "Here Is The Curve!" There are more interesting comments.

Koslowski's opponent is a pensioned planar surveyor Rayism 24b. As MCToon said: "Rayism is a planar surveyor so doesn't know anything about geodetic surveying."

Yet MCToon's discussion with Rayism 24b is very entertaining to watch. It's originally aired on MCToon Live under the name "Flat earther, planar surveyor, Rayism 24b debate". The comments (e.g. Jesse Koslowski) are worth to read.

This video can be found also on Toon Show 26.11.2021 as "FE Debate with planar surveyor Rayism 24b". There's new interesting comments again.

 

[Pertti Niukkanen]

What could be more convincing than Soundly's videos and photographs, or Jesse Kozlowski's measurements and calculations, with which he was able to determine the Earth's radius with 5 % accuracy? I hear flat-earthers say: Videos and photos can be faked, measurements can be faked and math proves nothing. Give me something real and tangible.

We could attach metal masts (or pylons) to the side of the Causeway Bridge every 5 kilometers or so. At the ends of the bridge, these masts could be 40 m long. At one end of the bridge is a tower where observer O can climb to see all the other masts. The picture shows eight red masts.

The length of these eight masts must be such that their tops are in the same horizontal geometric straight line. How to do this? I can't say, but geodetic surveyor Jesse Kozlowski sure knows the right tools (theodolites, etc.)

There's a bright red light at the top of each mast and a sensor which measures the distance to the water. The readings of the distance are displayed at the masts on some kind of light board so that the drivers on the bridge can see them.

What would a flat-earther say if he saw the reading drop as he approached the middle of the bridge? In the middle, it is almost 30 m less than at the end of the bridge. He would probably say that the tops of the masts are not on the same geometric line. Then he can climb to the observation tower O where he can look at the situation with a powerful telescope.

There's a problem though. Refraction raises objects on a same geometrically straight line so that the farthest ones raise more.

In the picture 1 below, there are two T-Towers seen from the height 10 m. Tower A is at the distance 10 km and tower B at 30 km. Their heights are such, that the observer sees their tops at his eye-level if refraction is ignored. In other words the observer and the tops of the towers are in the same horizontal plane.

In the picture 2 the standard atmospheric refraction (Std-Atm) is taken into account. Now the farther tower B is seen as higher. (See: http://walter.bislins.ch/bloge/inde...0.17051915-1~0.0065-12-11012.0493-114.935-9-4 )

So the flat-earther looking through a telescope gets his suspicions confirmed. The lights are not in the same height.

If the masts also had adjustable green lights, they could be lowered so that observer O sees them at the same height. I can't calculate how big this lowering is at each mast. My guess is that it is very small compared to the height of the mast. So the FE-driver on the bridge sees also the green readings drop clearly as he approaches the middle of the bridge. Is this enough to convince him that the bridge is not "flat"?

I thought I found a sure and concrete way to show the curve. But then came refraction. It always plays into the hands of flat-earthers, by reducing hidden heights, etc. I hate refraction.

 

[Mendel]

There's a bright red light at the top of each mast and a sensor which measures the distance to the water. The readings of the distance are displayed at the masts on some kind of light board so that the drivers on the bridge can see them.

You're suggesting a modern reimagining of the 1838 Bedford Level experiment (wikipedia), that resulted in an 1870 bet that ended with a court case and a Flat Earther imprisoned for threatening to kill the surveyor who won the bet.

A similar experiment was conducted by Jeranism in 2017 or 2018:

Article:

In about 10 tries, with the light held waist-high at 17 feet above water we never clearly saw it through the center panel hole. On one of the attempts, maybe the fourth of ten, we clearly saw it when Enrique lifted it over his head. On that one, Jeran asked him to raise it and lower it a few times, and it would appear when Enrique raised it and vanish when he lowered it. That was the "gasp" moment. Jeran said, "that's interesting." I noted it was the prediction for a round earth.

Source: https://flatearth.ws/curvature-analysis-jeran-campanellas-experiment-featured-in-behind-the-curve

You may conclude from this that, while it doesn't fail to show the globe, this type of experiment fails to convince die-hard Flat Earthers.

 

[Pertti Niukkanen]

You're suggesting a modern reimagining of the 1838 Bedford Level experiment (wikipedia), that resulted in an 1870 bet that ended with a court case and a Flat Earther imprisoned for threatening to kill the surveyor who won the bet.

In principle, yes. All curve tests are actually reruns of the Bedford Level experiment in one form or another. Of course, they won't convince die-hard flat-earthers, but I'm still searching for a way to make it harder for them to deny the results.

It is easy for flat-earthers to make one-off tests questionable afterwards. I have in mind some more permanent arrangement, where the curve would be seen all the time right in front of everyone's eyes. Here is my new idea.

As a foundation, you could build a 10 km long, geometrically completely straight "wall" and on top of it an open "trough" with a rectangular cross-section made of transparent plastic or glass. When water is poured into this trough, it runs off the ends of the trough but rises in the middle to a height of almost two meters.

The ends of the wall should also be in the same gravitational potential. It means that a spirit level would be in balance between the ends. According to the principle of "communicating vessels", you can use a 10 km long water pipe (or hose) as a spirit level. When the straight base-wall is ready, this can serve also as a test of the sagitta. It needs just a side pipe at 5 km.

It takes a lot of water to fill this trough. If the width of the trough is 1 m, it takes about 13080 cubic meters of water before the "overflow" starts. You may also use smaller cords c to demonstrate the curve with less water. In the table the length of the base (chord c) is given in kilometers, the sagitta s in centimeters and the corresponding volume of water at the trough width 1 m in cubic meters.

c (km) –– s (cm) –– V (m^3)
1 –––––– 1.96 ––––– 13.1
2 –––––– 7.85 –––– 104.6
3 ––––– 17.7 ––––– 353.2
4 ––––– 31.4 ––––– 837.1
5 ––––– 49.1 –––– 1635.0
6 ––––– 70.6 –––– 2825.3
7 ––––– 96.1 –––– 4486.5
8 –––– 126 –––––– 6697.0
9 –––– 159 –––––– 9535.4
10 ––– 196 ––––– 13080.1

The most important part in building the base is its "absolute" straightness. Geodetic surveyors and engineers have surely their means to ensure this. The bigger problem may be how to get the flat-earthers to believe that too. There needs to be a simple way to quickly demonstrate the straightness whenever someone asks about it. This I leave on my thinking cap.

This would be an undeniable and tangible comparison between the curvature of a spherical earth and the straightness of a flat earth. No questions about refraction or other atmospheric conditions. You may almost feel as if you are touching the curve.

As a family attraction this "Curve Aquarium" could have great pedagogical value. The children can see the curve literally "nose on the glass". Why hasn't this already been done to promote public education?

 

[Ann K]

Regarding the public-media flat-earthers, quibbling about the amount of the drop is unnecessary, isn't it? Any significant drop shows that the earth is not flat, and if a FE is not convinced by just the picture of the Lake Pontchartrain bridge, it seems unlikely that any more complicated demonstration would convince him. Putting actual numbers to the curvature is difficult because it requires getting imprecise and changeable refraction corrections into the equations, so when they start talking about that they are just distracting from the basic question. Most of them creating videos now seem to be in full "baffle them with bullshit" mode. They can be amusing, though...

 

[Mendel]

. I have in mind some more permanent arrangement, where the curve would be seen all the time right in front of everyone's eyes.

There's a number of Foucault pendulums installed around the Earth, they still don't believe it rotates.

And that's a much more obvious demonstration than your 2m on 10 km sagitta that nobody can verify without tools.

You might as well paint a straight line on the side of the Pontchartrain bridge—which would probably, due to proximity to water, not look straight some of the time, which will engender dozens of "black swan" videos...

 

[Pertti Niukkanen]

I still have some ideas for my "Curve Aquarium". As I said, there needs to be a simple way to quickly demonstrate the straightness of the base whenever someone asks about it.

There could be a completely straight vacuum tube through the base. It is made of steel and has transparent circular bases (bottoms) with diameter of, say, 50 cm.

If you look through this tube, the other end appears as a point of light with an angular diameter of 0.172 minutes of arc. This is about 6 times the angular diameter of Ganymede, the largest moon of Jupiter. Ganymede can be observed with ordinary binoculars.

I think the other end of the vacuum tube can be seen through a telescope as a small circle with even some detail. Some of the most powerful amateur telescopes, such as CELESTRON C14 SC XLT, are certainly sufficient.

So a flat-earther needs just look through the telescope to see the straightness of the base. If he still suspects some fraud, he could have his FE-friend at the other end. The friend could do what the observer asks with the cell phone (perhaps wave or block the entire view).

This is very simple. First check the straightness with the telescope, and then walk five kilometers to check the curve. Refraction cannot give excuses for curving, because there is no refraction involved. So no chance for black swans either.

As Mendel said above, there are 4 km long vacuum tubes at LIGO: "Precision concrete pouring of the path upon which the beam-tube is installed was required to counteract this curvature". If we could somehow use such a tube as reference for the base of Curve Aquarium, the sagitta would be 31.4 cm.

At least LIGO Hanford in Washington State offers free tours to the public every month. These tours are kind of family attractions with educational purposes too. So it would be fun if you could watch also Earth's curve during these visits. https://www.ligo.caltech.edu/WA/page/lho-public-tours

In this layout the connection to Earth's shape is obvious, much more so than with Foucault's pendulum. It also provides a side view of the curve, which might be impossible in any other way. It could be also a much needed demonstration for a layman (flat-earther or not) of the geometry and dimensions of the Earth.

Of course my suggestions are not to be taken quite seriously. I don't think that any of the world's many billionaires is eccentric enough to build my 10 km long Curve Aquarium (not to mention LIGO). But as a "gedankenexperiment" it might work as well, I guess.

 

[Mendel]

It also provides a side view of the curve, which might be impossible in any other way.

You literally get a side view of the curve any time you look at the ground. The problem is that the curvature is so very slight.

Some wide enough communicating pipes installed next to a LIGO arm might actually be doable and interesting.

In this layout the connection to Earth's shape is obvious, much more so than with Foucault's pendulum.

Yes. Obviously the pendulum only shows directly that the Earth turns, because its plane of motion turns. (The shape of the Earth is an indirect result because the rate of turn depends on the latititude.) But it is this obvious demonstration of the Earth's motion that still meets with denial, so don't expect your curve aquarium to be more convincing.

 

[Pertti Niukkanen]

All discussion forums have the same problem. A new member asks a question or opens a new thread about some old topic discussed heavily before. Repeating the same answers can be quite frustrating and annoying for old members.

As @Rory said: "And pretty much everything is here on Metabunk - but perhaps not so easy to find without a real trawl through the forum." Thanks for your "spreadsheet attached"-list. It's very useful. https://www.metabunk.org/search/539836/?q=spreadsheet+attached&c[users]=Rory&o=relevance

When I searched for "Rowbotham" I got many old threads on Bedford Level experiment, eg:
– Attempt at Recreating Rowbotham's Bedford Level Experiment by Flat Earth Believers (Rory, Jun 22, 2016)
https://www.metabunk.org/threads/attempt-at-recreating-rowbothams-bedford-level-experiment-by-flat-earth-believers.7710/
– Where and How could the Wallace Experiment Easily Be Repeated? (Mick West, Sep 12, 2016)
https://www.metabunk.org/threads/where-and-how-could-the-wallace-experiment-easily-be-repeated.7920/
– Recreating the Bedford Level Experiment (Rory, May 21, 2018)
https://www.metabunk.org/threads/recreating-the-bedford-level-experiment.9729/

After reading these threads, I'm not as sure about the ease of this experiment as I was before. The story of Alfred Russel Wallace and John Hampden is not very encouraging either.

I also thought of using a long water hose to demonstrate the sagitta, but noticed that this topic has been discussed before too:
– Using a very long water level to measure Earth's curvature (danno, May 14, 2018)
https://www.metabunk.org/threads/using-a-very-long-water-level-to-measure-earths-curvature.9710/

In the comments there is a link to Adrian Chetwynd's 2017 video: "Earth is not flat. Flat water is curved!". He did a hose test at the length of 1 km. Then the sagitta is only about 2 cm. The idea is fine, although the straight reference line is the biggest problem here too. He said this was just a preliminary test for a more controlled experiment at longer distance. However, nothing has been heard from him since then.

Another suggestion for an experiment mentioned there is from Sly Sparkane 2019: "Flat Earth: Bending Water Test Funding"


Source: https://www.youtube.com/watch?v=jh9Q42ZoOLo


The proposal was not received with unanimous enthusiasm. In the video's comment section, engineer George Hnatiuk criticized heavily the arrangements of the experiment. I thought the experiment was never done, but now I'm not quite sure. Sky Sparkane's YouTube channel has many "Bending Water Test" updates from 2019, but I haven't watched them yet. Does anyone know how this case ended?

 

[Ann K]

Another suggestion for an experiment mentioned there is from Sly Sparkane 2019: "Flat Earth: Bending Water Test Funding"

I get nothing but error messages from that video. Could you summarize the basics?

 

[Pertti Niukkanen]

I get nothing but error messages from that video. Could you summarize the basics?

Here is Sly Sparkane's experiment in five screenshots from the video.

At the distance 1600 m the geometric sagitta is 5.02 cm, so I don't know where he gets 4 inches (= 10.16 cm). Besides, he doesn't care about refraction and marks straight line on the tubes as seen with the camera. So he shall get a smaller, "refracted" sagitta, which is with standard refraction about 4.30 cm.

You can compare this with my thought experiment on Lake Pontchartrain Bridge. There the observer O sees the line of green lights as a straight line, although they actually curve down from the horizontal plane. However, the effect of refraction is small and ignoring it will not destroy the experiment.

Critical comments are mainly focus on the practical problems of conducting the experiment. Does Sparkane realize how big a job he has taken on? Here are some hard comments from engineer George Hnatiuk:

------------------------
Sly,
Before going public with this, you could have asked for engineering help/opinion but you did not. Now you will have to live with the embarrassment and consequences that are sure to arise if you attempt this. Talk to Rumpus and Phil Nye for each have discussed this with me and can detail the problems to you that I have identified along with those that they have which you apparently have not considered. This is a good "thought" experiment but as with many thought experiments, that is all it is good for. Any practical implementation may not be possible with a thought experiment. This is going to be very difficult to carry out in actual practice.
GH Feb 01,2019 6:44pm

Sly,
I did read the pinned comment before posting any comments and nothing in there indicates that you sought profession review of this test and its implementation. You have in that comment expressed some of the standard issues common to all tests but little related to the specifics of this test.
All you say is setting the marks to line up will be difficult but did not discuss how you would actually accomplish it. Do you not think it would be prudent to detail such an important issue before asking others to contribute money in support of the project? Last thing you need to do is risk the money of others thinking you can solve this issues on the fly. I would want to know all the details so I can access the risk associated with success or failure before investing in a project. Without that information, you are no better than FECORE and their failed projects and acting irresponsibly. This is your reputation you are putting at risk besides the contributions of others. Your choice.
GH Feb 01, 2019 7:24pm

Sly,
You have more likely than not performed any preliminary investigations for if you had, you would have detailed how you would line up the marks rather than being so vague. Not only that, you would have understood that a 10mm tube would not work over 1600 meters. Ridiculous.

Sly,
Do not get this wrong. I written you here to caution you before you embark on this project so it does not blow up in your face. I am a damn good engineer and can see many difficulties that you will encounter and It does not seem that you have thought this out thoroughly or consulted anyone with an engineering background.
GH Fe, 02, 2019 11:44am
-----------------------

I don't know how the story continues. Was the test finally done and what were the results? Maybe they are found on Sly Sparkene's You Tube channel https://www.youtube.com/channel/UCcJ-sg7yIH5osx4pGcyVZMw.

There's also this video that Ann K couldn't open. You only have to scroll back about three years. I hope it opens this way.

 

[Mendel]

I remember the experiment was done on the bank of some river in Austria or southern Germany, but suffered from the small diameter of the plastic tubes which impeded the levels equalizing when the contraption was filled. 2019 or 2020?

 

[Pertti Niukkanen]

I remember the experiment was done on the bank of some river in Austria or southern Germany, but suffered from the small diameter of the plastic tubes which impeded the levels equalizing when the contraption was filled. 2019 or 2020?

So George Hnatiuk was right when he said that piping will be a problem.

I don't think that we amateurs can do such an experiment successfully. We need top professionals and top equipment and especially that strange billionaire to be interested in this crazy idea. The project budget would be then unlimited. The professionals will probably wonder about this kind of waste of time, but the salary offer would be one you can't refuse.

 

[Mendel]

So George Hnatiuk was right when he said that piping will be a problem.

If you are equalizing, you are going to near zero pressure differential driving the water flow, at which point stuff like wind blowing across the open ends becomes noticeable.

I don't think that we amateurs can do such an experiment successfully.

Define success.

 

[Pertti Niukkanen]

Define success.

The experiment is successful when it answers the question for which it was made. The reason for the failure of the experiment can be the practical difficulties of the proposed test arrangement, e.g. sub-optimal test terrain, lack of sufficiently high-quality test equipment, etc. Many reasons that could be eliminated with enough money (which amateurs rarely have).

If the test is conducted anyway, the result may be that it does not give a clear answer to the given question or verify/falsify a possible hypothesis. That's what I meant by the unsuccessful test, nothing special, just the usual stuff.

 

[Mendel]

The experiment is successful when it answers the question for which it was made. The reason for the failure of the experiment can be the practical difficulties of the proposed test arrangement, e.g. sub-optimal test terrain, lack of sufficiently high-quality test equipment, etc. Many reasons that could be eliminated with enough money (which amateurs rarely have).

If the test is conducted anyway, the result may be that it does not give a clear answer to the given question or verify/falsify a possible hypothesis. That's what I meant by the unsuccessful test, nothing special, just the usual stuff.

The easier test is to take a plastic tube and some water up a seaside mountain, fill it up, and then sight across the ends to the horizon, which then will appear to be below eye level both ways.

 

[Pertti Niukkanen]

The easier test is to take a plastic tube and some water up a seaside mountain, fill it up, and then sight across the ends to the horizon, which then will appear to be below eye level both ways.

Yes, that surely proofs the drop of horizon.

I just talked with a flat-earther who accepts this result, i.e. he admits that the FE-slogan "the horizon always rises to eye-level" is false. Yet he doesn't accept that the horizon is curving. In his logic there is no connection between these things.

So I'm still looking for some test to show the sagitta. Here is my latest (and hopefully last) idea.

A highly tensioned cable is geometrically quite straight. It's not straight enough though to be the straight reference line which I need. Gravity takes care of that.

What if the cable had the same density as water? It would behave like a weightless object and stay where you put it in the water. Then it would be easy to tighten the cable without much force. Wouldn't it be straight then too? Maybe this works at 10 m. It should be quite easy to test with the "Rory's method" in some transparent tube. If it works, maybe it works at 10 km too?

If you think this idea is crazy, you are probably right.

 

[Mendel]

What if the cable had the same density as water? It would behave like a weightless object and stay where you put it in the water. Then it would be easy to tighten the cable without much force. Wouldn't it be straight then too? Maybe this works at 10 m. It should be quite easy to test with the "Rory's method" in some transparent tube. If it works, maybe it works at 10 km too

in 10 km of open water, the currents will destroy the straightness of your cable

and even if you could get it to be straight (e.g. by submerging it in the Bedford canal), the FEers would simply say tbe cable sags and the water level is straight when you show them the sagitta

 

[Mendel]

In his logic there is no connection between these things.

this is the power of denial

the only people I know of who beat FE are those who got off their asses and worked through something themselves