Comparing flat Earth and spherical Earth from a geometric point of view

[Pertti Niukkanen]

Here's the homemade test I suggested above. The idea is to observe the tip of the shadow of a stick etc. and mark its location every hour. The stick does not have to be straight or even completely vertical. The platform does not have to be completely horizontal either, but it must be flat for the follow-up test.

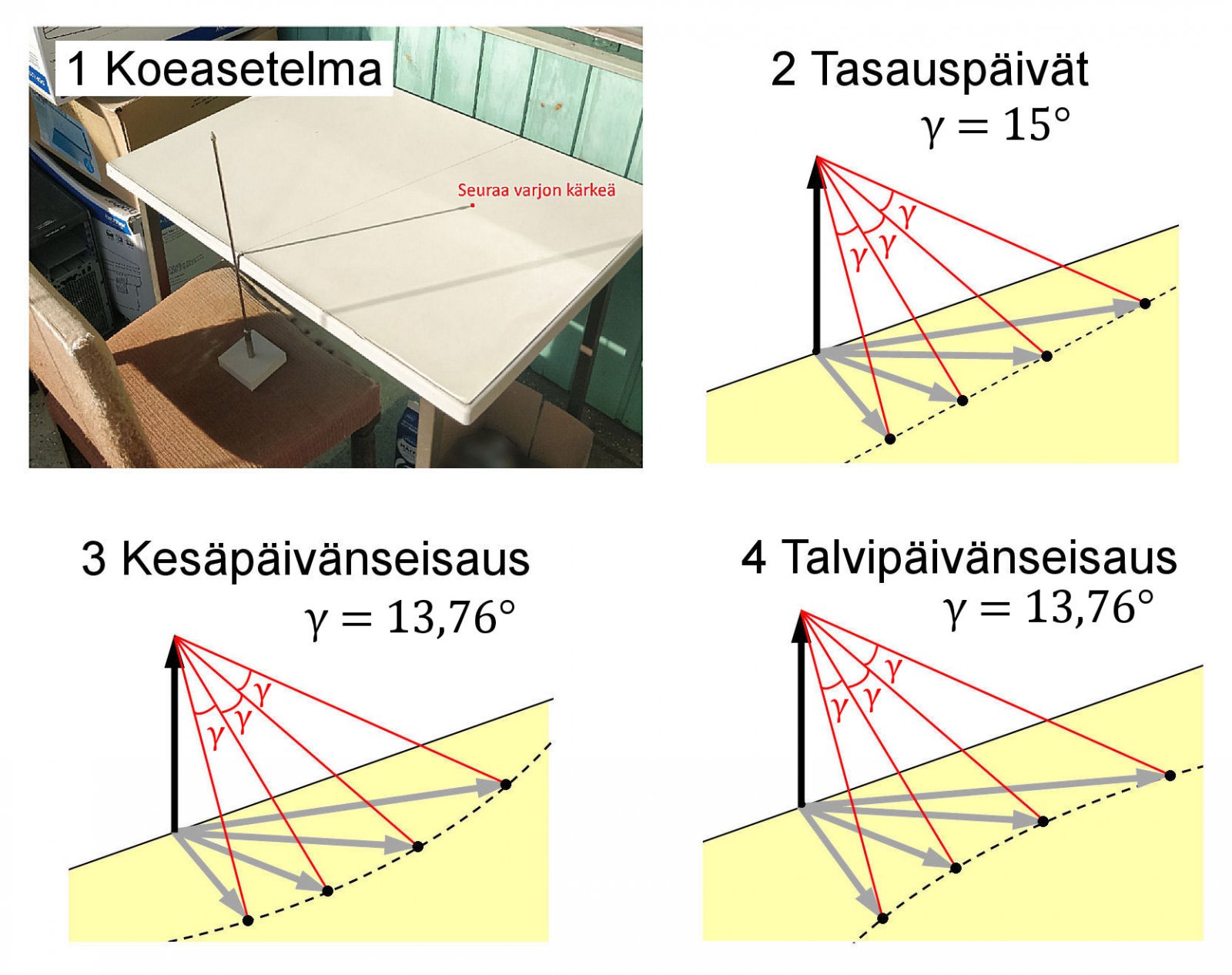
Picture 1 shows my version from a year ago. It had a miniature flagpole as a stick, the tip of which cast a shadow on the flat table. I marked the tip of the shadow with a marker on the table every hour.

Figure 2 shows the expected result of an experiment conducted at the vernal equinox. If you tighten the (red) threads from the tips of the shadows to the tip of the stick, you can see that the angles between the threads are all 15°. In addition to this, the tips of the shadow line up.

Especially the latter result is fatal for FE theory. The Sun rotating in a circle above the flat Earth cannot possibly produce such a straight line. The tip of the shadow should draw a circle.

(Admittedly, I did nothing but the latter test myself at that time, which succeeded as expected. I was too lazy to measure the angles. I hope you find an easy way to measure them.)

Figure 3 shows a similar test done on the summer solstice. In this case, the angles between the wires should be 13.76°. (You can probably be satisfied if you get a result of approx. 14°.) Now the tips of the shadow do not draw a straight line, but settle on an arc, which, strictly speaking, is a hyperbola.

Figure 4 shows an experiment done on the winter solstice. Even then, the angles between the threads are 13.76°. Even now, the tips of the shadow are placed on an arc, which is a hyperbola. This time it just opens in the opposite direction as in experiment 3. This is even more impossible in the FE model.

 

[Pertti Niukkanen]

It looks to me like you were going somewhere else, though?

You are right. I actually wanted to criticize a meme I found on the fb group "Official Flat Earth & Globe Discussion"

The meme was created by debunker Michel Toulouse (MT). He is a competent debunker, but this time his meme promises too much: "Anywhere on Earth, any season, all year long, any time of the day, a stick will show you the Sun appears to move 15° per hour."

However, the angle test shows that this only happens on the equinoxes. Well, blunders happen to debunkers too.

 

[Mendel]

(Admittedly, I did nothing but the latter test myself at that time, which succeeded as expected. I was too lazy to measure the angles. I hope you find an easy way to measure them.)

I'd have mounted the camera vertically if I had thought of that. But doesn't this require the surface to be equatorial? The tilt would skew the angles, methinks.

I put the camera on a tripod and did a time lapse recording, adding the track in the editor later.

Source: https://youtu.be/KLb1QtRZlzg

 

[Pertti Niukkanen]

I'd have mounted the camera vertically if I had thought of that. But doesn't this require the surface to be equatorial? The tilt would skew the angles, methinks.

I think you are right. However, the camera must be quite high, so that the images are not distorted by perspective.

 

[Pertti Niukkanen]

I'd have mounted the camera vertically if I had thought of that. But doesn't this require the surface to be equatorial? The tilt would skew the angles, methinks.

When I thought about it more, I began to have doubts. Now I think you can't measure the angles just from the pictures you get with the camera.

In the Toulouse meme, the angle between the tightened wires must be measured. In this case, the shape or position of the platform does not matter, nor does the shape or position of the stick (gnomon). This much is correct in the meme.

Let's consider situation A. In that case, the stick is straight and vertical. Suppose you have the camera high up exactly above the stick. The camera now sees shadows as straight lines, regardless of the shape of the platform. Let α be the angle between them in the photo. If you had installed the red wires, they would appear to be on top of the shadows, so in the camera image the angle between them is also α.

The angle α is the horizontal projection of the desired angle formed by the red wires (let it be β). This projection angle α is always bigger than the angle β. However, the angle β cannot be calculated if we do not know the height of the Sun. (E.g. in picture A, β = 15°. Let's assume that the height of the sun is 32°. I calculated that then α = 17.8°. I hope I calculated correctly.)

So I feel that it is not possible to determine the angle β from camera images alone. It has to be done by measuring the angle between the red wires manually (at least in the home test).

The question was surprisingly difficult for me and I am not at all sure that my explanation is correct. So if you do the test your own way, let us know how it went.

 

[Mendel]

Imagine being on a Pole. If you use a 90⁰ vertical gnomon here, on a flat level surface, you always get 15⁰ per hour for the shadows. This is because basically the sun stays where it is, maintaining its elevation, and the paper simply turns 15⁰ per hour as the Earth turns, for one 360⁰ circle per day.

An equatorial mount is motor-driven tripod for astronomical observations, where you set up the axis parallel to the Earth axis, and then set it to rotate 15.04⁰ per hour which makes it immobile with respect to the stars: basically the same as if you had set it up at the pole (until the ground gets in the way).

Source: https://www.youtube.com/watch?v=1zJ9FnQXmJI

So all you need to do is determine your latitude L, the angle θ=90⁰-L, and incline your paper by that angle by elevating the edge of it that points toward the equator. Then the shadows of a vertical gnomon will also be at 15⁰.

Note that the meme is still false.
View attachment 66793
Imagine summer solstice at the North Pole, piece of paper with a vertical gnomon, mark the shadows every hour, for 24×15⁰=360⁰ on the paper. However, the spatial angles are smaller (because the two sides enclosing the angle are longer) than the angles on the paper, so they are less than 15⁰. They only match on the equinox.

 

[Pertti Niukkanen]

So all you need to do is determine your latitude L, the angle θ=90⁰-L, and incline your paper by that angle by elevating the edge of it that points toward the equator. Then the shadows of a vertical gnomon will also be at 15⁰.

So this is an equatorial sundial. However, in order for the direction of the shadow to change 15 degrees per hour, the gnomon must be perpendicular to the hour disk (i.e. not vertical elsewhere than at the pole).

However, the spatial angles are smaller (because the two sides enclosing the angle are longer) than the angles on the paper, so they are less than 15⁰. They only match on the equinox.

Yes, e.g. on the summer solstice, the angle is approx. 13.76 degrees. However, we still have the problem of how to demonstrate this experimentally. The "red threads method" certainly works, but are there other ways?

By the way, what do you mean by "Note that the meme is still false"?

 

[Mendel]

So this is an equatorial sundial. However, in order for the direction of the shadow to change 15 degrees per hour, the gnomon must be perpendicular to the hour disk (i.e. not vertical elsewhere than at the pole).

Technically the gnomon need not be perpendicular, but then it's not at the center of the circle. The shadow of the tip will move on a circle (as it is supposed to on FE if you don't tilt your paper), and measured from the center of that circle, you still get the 15⁰ per hour angle.
Using a gnomon aligned with the axis of the Earth ensures that it intersects the paper at that center.

Yes, e.g. on the summer solstice, the angle is approx. 13.76 degrees. However, we still have the problem of how to demonstrate this experimentally. The "red threads method" certainly works, but are there other ways?

Align the optical axis of the camera with the axis of the Earth.

By the way, what do you mean by "Note that the meme is still false"?

The 15⁰ angle indicated on the meme is not 15⁰.

 

[Pertti Niukkanen]

Align the optical axis of the camera with the axis of the Earth.

I hope you will do the test this way and let us know how it went.

The 15⁰ angle indicated on the meme is not 15⁰.

It is correct on the equinoxes though, right?

 

[JMartJr]

Critique welcomed...

BUT hang on just a minute...

Edit: Image 2 replaced after deleting erroneous reference to Paris.

 

[Mendel]

It is correct on the equinoxes though, right?

No.
Take a flat, level paper and a perpendicular gnomon. Sun rises exactly East, sets exactly west 12 hours later = 180⁰ / 12h on the paper with the shadow = 15⁰ per hour. The tip to paper legs are longer, making the angles at the tip smaller.

It only matched on the pole on the equinox because then the paper is parallel to the shadow.

 

[Pertti Niukkanen]

No.
Take a flat, level paper and a perpendicular gnomon. Sun rises exactly East, sets exactly west 12 hours later = 180⁰ / 12h on the paper with the shadow = 15⁰ per hour. The tip to paper legs are longer, making the angles at the tip smaller.

It only matched on the pole on the equinox because then the paper is parallel to the shadow.

This is a horizontal sundial with the gnomon perpendicular to the hour disk. This sundial is dependent on your location. The hour disk is different at different latitudes. Only on the poles are the angles equal (15 degrees per hour). These hour discs work all year round, regardless of the time and direction of sunrise or sunset.

Let's apply my formula (1) to the angular displacement of the Sun in an hour. Then α = 15° (Earth's rotation per hour relative to the Sun). The angle β is the Sun's declination (the Sun's angular distance from the celestial equator).

The formula (1) gives the angle γ, which is the angular displacement of the Sun per hour as seen from Earth (the angle between the red wires). It varies depending on the season, so the Sun's declination β for that time must be known. On the equinoxes β = 0°, on the spring solstice β = 23.4° and on the winter solstice β = -23.4°.

The formula does not take the latitude into account. You get the same result no matter where on the globe you measure the angle between the red wires. Take the test tomorrow. I bet you get 15 degrees.

 

[Mendel]

These hour discs work all year round, regardless of the time and direction of sunrise or sunset.

I'd like to disagree.

I've seen a sundial built by a maths/physics teacher with a movable gnomon (the observer) that depends on the time of year.

Note also that your angle γ would change with the elevation of the sun if the hour disk worked year-round.

 

[Pertti Niukkanen]

I'd like to disagree.

I've seen a sundial built by a maths/physics teacher with a movable gnomon (the observer) that depends on the time of year.

Note also that your angle γ would change with the elevation of the sun if the hour disk worked year-round.

In this experiment we can forget how sundials work. The question is only about the size of the angle γ. My "artwork" below tries to show that the gnomon can be any shape (e.g. a crooked tree). The shape of the platform doesn't matter either (steep and uneven rock slope). The direction of the red arrows is the same regardless of these factors. And so is the angle γ.

I will try to do this string test tomorrow, if the weather in Helsinki permits. I'm sure I'll get a result of 15 degrees per hour. I also believe that you will get the same result no matter where you make the test.

 

[Mendel]

On the equinox, G=P and α=γ=15⁰.

 

[Pertti Niukkanen]

On the equinox, G=P and α=γ=15⁰.

So we agree? The string test tomorrow will result γ = 15°.

 

[FatPhil]

View attachment 66836
On the equinox, G=P and α=γ=15⁰.

If GP || earth's axis, and GP _|_ PA and PB, then I'm curious what physical thing plane PAB is supposed to represent, and consequently what A and B represent. If P is at ground level, then A and B are below ground level, which is not normally where you find the ends of gnomon shadows.

 

[Pertti Niukkanen]

It's cloudy in Helsinki today, so the test has to be postponed.

My formula calculates the angle γ for all days when we know the Sun's declination β on that day. In the table, the γ-angles are calculated for the period 20.3.2024 – 20.6.2024. Unfortunately, I don't know how to calculate the change in declination as a function of time (except on equinoxes and solstices). So I took the Sun's declinations directly from Stellarium. I used Helsinki time 05:14:00 as the spring equinox and continued every 24 hours from there.

I think my table is quite accurate for all places on earth. It can be pretty valid in other years as well, except maybe the last decimal.

The diagram shows the change in angle γ visually. It resembles a sine curve. At the moment the change is very slow, so you will probably get γ = 15° in the test for several more days. You can make the test at other times as well. For example, 25.5. according to the table, the result would be 14°.

 

[Pertti Niukkanen]

I searched the internet for "solar declination calculators" and found this: https://solarsena.com/solar-declination-angle-calculator. This site also has many formulas for calculating the Sun's declination, e.g. the following:

"In the above formula, d is the number of days since January 1st (UTC 00:00:00). For example, On March 3rd (UTC 00:00:00), d = 31 + 28 + 2 = 61. On December 31st (UTC 00:00:00), d = 364." So March 20st is day number 78.

This formula does not take leap years into account. So this year March 20st is day number 79. When I took this into account and applied the formula, I got pretty much the same declinations as in my table (taken from Stellarium). The maximum difference was approx. 0.17°. The compatibility is quite good when we also remember that the equation assumes the earth orbits around the sun in a perfect circle.

My declination table above is probably more accurate than the values given by the formula because its values are "real time" given by Stellarium. So it probably gives quite accurate values also for the angle γ during this spring (for all places on earth). However, it cannot be applied to next year because the dates do not match. I probably also overestimated the accuracy of the table. There can be an error even in the first decimal place.

In any case, it is true that on equinoxes γ = 15° and on solstices γ = 13.76°. It can also be said that the change in angle γ roughly follows the shape of the graph below every year.

 

[psikiwi]

So on a slightly different tangent...
Am I correct, that at the equinox, the sun rises due east, and sets due west, for everywhere on the globe. How can this be explained, on the FE disc map (AE projection, as originally pointed out in this thread)? The sun must be 'setting' in 100000 different places, from Helsinki to Cape Horn, to be truly west, of each/any of the locations.
Is this a new nail in the FE coffin lid? (I don't have the time right now, let alone the skills, to try and draw anything as explanation, if my words aren't making sense.)

 

[psikiwi]

If GP || earth's axis, and GP _|_ PA and PB, then I'm curious what physical thing plane PAB is supposed to represent, and consequently what A and B represent. If P is at ground level, then A and B are below ground level, which is not normally where you find the ends of gnomon shadows.

As I read the exchange above, it seems there is some talking past each other. In brief, it doesn't matter where the ends of the shadows are: on, in or above any plane/surface.
IF an observer is located at the end of suns ray, just grazing the tip of any given sharp object (tree, flag-pole, pencil on a desk), AND 1 hour later is positioned anywhere they like, but still along a the ray of sunlight grazing the same 'gnomon' tip, THEN the angle subtended at the gnomon tip is 15 degrees. (Within cooee, given some variations as highlighted in numerous sections above.)

 

[Scaramanga]

I've seen many pieces of dubious reasoning flat earthers use to get round the distance problems on a flat Earth. But the one thing they cannot get round is the Coriolis effect.

Firstly, because flat earthers regard the earth as stationary and the Sun going round it...there should be no Coriolis effect at all. So flat earthers have to explain why any such effect exists at all.

Secondly, the Coriolis effect as observed is a direct result of the Earth being a sphere. That includes not only the strength of the effect at differing latitudes but also the fact that the effect reverses in the southern hemisphere. There is no geometry other than a sphere that explains this, and a flat earth model simply cannot explain the Coriolis effect reversing at the equator.

 

[FatPhil]

So on a slightly different tangent...
Am I correct, that at the equinox, the sun rises due east, and sets due west, for everywhere on the globe.

It's a good question, and one I only had a feel for, but felt that I needed a proof (or disproof) of. Fortunately it didn't take long, and I thought I'd share.
In brief: It's true because the poles are side on to the sun.
Long form: Imagine the plane going through the middle of the earth, perpendicular to the sun. That plane cuts through the poles, and forms a great circle. Therefore it must be a whole line of longitude. Therefore anyone standing just on the far side of that line must look perpendicularly across the line in order to see the sun rise or set. Therefore it's due east, or due west, for them. And a that's true for any line of latitude during the day, it's true for every place on earth that day.
I'm often terrible at explaining things, if anyone can reword for better clarity, please do.

Thank you for making me think, I was feeling a bit of a zombie after two big beer-related events yesterday.

 

[AmberRobot]

I've seen many pieces of dubious reasoning flat earthers use to get round the distance problems on a flat Earth. But the one thing they cannot get round is the Coriolis effect.

Firstly, because flat earthers regard the earth as stationary and the Sun going round it...there should be no Coriolis effect at all. So flat earthers have to explain why any such effect exists at all.

Secondly, the Coriolis effect as observed is a direct result of the Earth being a sphere. That includes not only the strength of the effect at differing latitudes but also the fact that the effect reverses in the southern hemisphere. There is no geometry other than a sphere that explains this, and a flat earth model simply cannot explain the Coriolis effect reversing at the equator.

Presumably, a Flat Earther would dare you to show them an experiment demonstrating the Earth's Coriolis effect, which really can't easily be done on a small scale (though there are some good videos of some people carefully preparing pools of very still water), just like their challenges of finding water sticking to a sphere or gas pressure without a container and other examples that require a massive change of scale to demonstrate.

Furthermore, they don't seem to be bothered with effects that have no plausible mechanism, such as the Sun and Moon orbiting in circles above the flat Earth with absolutely no mechanism explaining why they do that. So, things like hurricanes spinning in certain directions could simply be a brute fact of the Earth, just like the orbiting Sun.

You cannot defeat Flat Earthers with reasoning. They do not appear to demonstrate scientific or mathematical reason beyond the simplest of platitudes, like their constant erroneous calls to "perspective" to explain away what obviously destroys their model.

 

[Pertti Niukkanen]

As I read the exchange above, it seems there is some talking past each other. In brief, it doesn't matter where the ends of the shadows are: on, in or above any plane/surface.
IF an observer is located at the end of suns ray, just grazing the tip of any given sharp object (tree, flag-pole, pencil on a desk), AND 1 hour later is positioned anywhere they like, but still along a the ray of sunlight grazing the same 'gnomon' tip, THEN the angle subtended at the gnomon tip is 15 degrees. (Within cooee, given some variations as highlighted in numerous sections above.)

You are absolutely right. It is exactly this - and only this - that I have tried to explain above.

 

[Pertti Niukkanen]

So on a slightly different tangent...
Am I correct, that at the equinox, the sun rises due east, and sets due west, for everywhere on the globe. How can this be explained, on the FE disc map (AE projection, as originally pointed out in this thread)? The sun must be 'setting' in 100000 different places, from Helsinki to Cape Horn, to be truly west, of each/any of the locations.
Is this a new nail in the FE coffin lid? (I don't have the time right now, let alone the skills, to try and draw anything as explanation, if my words aren't making sense.)

You are right. At the equinoxes, the sun rises exactly in the east and sets exactly in the west everywhere on Earth. Also, its altitude at noon is 90 minus the latitude of the location.

So, at the equator on the equinoxes, the sun rises exactly in east, is exactly at zenith at noon, and sets exactly in west 12 hours later. During all this time, the Sun's angular diameter is approx. 0.53 degrees.

Every flat-earther would have observed this a couple of days ago at the locality A (see picture below). But would he have believed his eyes? What should he have observed according to his own model?

According to the FE model, the sunrise in A means that the Sun suddenly appears as a small point (angular diameter approx. 0.19 degrees) in the north-eastern sky at an altitude of approx. 20 degrees. From there it continues its course until it is exactly at the zenith above point A at noon. In this case, its angular diameter is approx. 0.57 degrees. This is the same order of magnitude as in the ball model. This is the only moment that the observations and the FE model roughly match each other.

After that, the sun continues its journey along the equatorial circle at an altitude of 5000 km. The sunset as seen from A means that the Sun disappears from view in the northwest direction. When it disappears, the altitude is approx. 20 degrees and angular diameter approx. 0.19 degrees.

These sudden "disappearances" are explained in the FE theory, e.g. as follows: The sun is so far away that its light gets tired over a long distance. The Sun can only shine for a certain distance. Without such explanations, it is impossible to understand why the Sun is not visible at night. Even then, its altitude is about 14 degrees (seen from locality A).

The FE model and observations are in sharp contradiction. I haven't seen a single reasonable attempt to resolve this conflict – and I'm unlikely to see one.

I think the FE coffin is already firmly closed. The flat-earthers just don't believe it. Just as little would they believe their own eyes when looking at the sun's path at the equator.

 

[JMartJr]

the equinoxes, the sun rises exactly in the east and sets exactly in the west everywhere on Earth.

Other than at the poles, where it just sort of skims along the horizon, and where East and West become indeterminate .

 

[Pertti Niukkanen]

It's a good question, and one I only had a feel for, but felt that I needed a proof (or disproof) of. Fortunately it didn't take long, and I thought I'd share.
In brief: It's true because the poles are side on to the sun.
Long form: Imagine the plane going through the middle of the earth, perpendicular to the sun. That plane cuts through the poles, and forms a great circle. Therefore it must be a whole line of longitude. Therefore anyone standing just on the far side of that line must look perpendicularly across the line in order to see the sun rise or set. Therefore it's due east, or due west, for them. And a that's true for any line of latitude during the day, it's true for every place on earth that day.
I'm often terrible at explaining things, if anyone can reword for better clarity, please do.

Thank you for making me think, I was feeling a bit of a zombie after two big beer-related events yesterday.

I made a "dynamic" model of the sun's paths on equinoxes and solstices for different latitudes. The model is easy to build. You basically just need a transparent hollow plastic ball, different colored markers and colored water.

Instructions for making the model can be found here: https://www.metabunk.org/threads/co...m-a-geometric-point-of-view.12591/post-280291

 

[Pertti Niukkanen]

An addition to my previous example.

In the FE model, the Sun never really sets or rises, but always goes around a circular path above the flat Earth at an altitude of approx. 5000 km. Even at midnight the Sun's altitude is approx. 14.03° and angular diameter approx. 0.14°. Why don't we see it then though?

 

[Pertti Niukkanen]

If GP || earth's axis, and GP _|_ PA and PB, then I'm curious what physical thing plane PAB is supposed to represent, and consequently what A and B represent. If P is at ground level, then A and B are below ground level, which is not normally where you find the ends of gnomon shadows.

If GP || earth's axis, and GP _|_ PA and PB , then the plane PAB is the equatorial plane. Mendel's sketch therefore depicts an equatorial sundial, where the angle α is 15° per hour. The angle γ is also constant per hour, but generally γ < α. As Mendel said: "On the equinox, G=P and α=γ=15⁰."

Mendel's sketch can also be used to derive a general formula for the angle γ. In my sketch, the angle β is the Sun's declination (the Sun's angular distance from the celestial equator). This way I derived a new formula (2) for the angle γ. It's simpler than the formula (1) that I derived before, but it returns exactly the same values.

Speaking of sundials, I have to correct my previous comment @Mendel: https://www.metabunk.org/threads/co...m-a-geometric-point-of-view.12591/post-312818

In a horizontal sundial, the hour disk is different for each latitude. However, this is not enough; the gnomon must be parallel to the earth's axis (as in the equatorial sundial). I didn't know this before. These customized sundials work all year round.

Here are the instructions for making a simple horizontal sundial: https://www.blocklayer.com/sundial. In the picture, the latitude is 20.46°. Would work e.g. in Tecolutla, Mexico or Vapi, India.

 

[Pertti Niukkanen]

Figure 1 shows the experiment I proposed above to determine the angle γ. In my test, the threads are attached slightly below the tip of the miniature flagpole. I marked the attachment point with a thin red plastic straw. This way, the "tip" of the shadow is a cross, which is more clearly readable (red dot in the picture).

I marked the "crosses" every hour with a marker on the surface of the table. Then I attached small nails at the marks and tightened the threads from them. The angle γ is now the angle between the wires.

According to the theory, on the equinox γ = 15°. However, I did the test only yesterday, 28.3. i.e. 8 days later. Then the angle should be (according to my calculation) slightly smaller, γ = 14.98°. It is worth repeating the test at the time of the summer solstice, when the angle should be clearly smaller, γ = 13.76°.

It was cloudy in Helsinki on the spring equinox and the cloudy weather just continued. Only yesterday 28.3. the sun was shining enough that I was able to make the test with the help of my friend Ilkka.

In the left picture, the "tips" of the shadows are already marked on the table. We got a clear mark at 10 a.m., 12 p.m. and 1 p.m. At 11 a.m. the sky was overcast, so that mark is missing. Fortunately, the marks 2, 3 and 4 were good enough for our measurements. In the pictures, Ilkka measures the angle between threads 2 and 3 with a protractor. In the picture on the right, you can see that the angle γ is approx. 15°. (Actually, it should be 14.98°, but of course our experiment is not capable of such accuracy.)

In addition, you can see from the picture on the left that the marks are no longer placed exactly on a straight line, as happens on equinoxes. After all, 8 days have already passed since the equinox.

Below is the measurement of the angle between threads 3 and 4. The result is still the same: the angle γ is approx. 15.

It is really worth repeating the experiment at the time of the summer solstice, when the angle γ is approx. 14° (more precisely γ = 13.76°). Even this modest test can clearly show the 1 degree difference. It also shows (at a qualitative level) that the "ball theory" works.

 

[Scaramanga]

Presumably, a Flat Earther would dare you to show them an experiment demonstrating the Earth's Coriolis effect, which really can't easily be done on a small scale (though there are some good videos of some people carefully preparing pools of very still water),

As an avid follower of storm chasers and also the various live storm chaser feeds, one consistent feature of northern hemisphere supercells especially across the great plains is their counter-clockwise rotation. Countless examples on video.

Do they rotate clockwise in the southern hemisphere ? Yes, indeed. There are less examples on video....but here is one....an excellent demonstration of the Coriolis effect...


Source: https://www.youtube.com/watch?v=1elXp0GhgDs

 

[FatPhil]

As an avid follower of storm chasers and also the various live storm chaser feeds, one consistent feature of northern hemisphere supercells especially across the great plains is their counter-clockwise rotation. Countless examples on video.

Do they rotate clockwise in the southern hemisphere ? Yes, indeed. There are less examples on video....but here is one....an excellent demonstration of the Coriolis effect...

Surely ballistic drop is a far easier demonstration of the coriolis effect, not requiring a stochastic dynamic system? Just fire east and west near the equator - fire west and the target will rise and come towards you, fire east, and the target will drop and move away from you. Yes, unfortunately, those two effects are in opposite directions, but all you need to do is show that east and west behave differently (and differently from firing north or south - those two can also be used to show a sideways coriolis effect, but alas air movement is much more of a problem side to side than it is up and down, hence drop being the clearer indicator).

You'll probably need a decent fraction of a kilometer, or a large sample size - go on, you know you want to, in order to see the effect with statistical significance.

Note, this is all theoretical: all I know is the maths, not the hardware. It *should* be possible to demonstrate at the hunting-rifle scale, it doesn't just apply to big guns like the Paris Gun.

 

[Scaramanga]

You'll probably need a decent fraction of a kilometer, or a large sample size - go on, you know you want to, in order to see the effect with statistical significance.

The only 'effect' here would be a SWAT team showing up.....as guns are not allowed in the UK. Though hunting rifles must be allowed with special permits.....as when mountain climbing in Scotland I've a few times had to call the land owner to make sure deer hunting parties were not active.

Do snipers need to take the Coriolis effect into account ? I'm not sure. What I do know is that on a smaller scale of a kilometer or less the Coriolis effect is far less active. That is why in the northern hemisphere you get a few percent of tornadoes that rotate clockwise....opposite to the Coriolis effect. I would imagine that a sniper bullet would be travelling too fast for the Coriolis effect to have any significant impact....but its an intriguing question.

 

[Pertti Niukkanen]

Do snipers need to take the Coriolis effect into account ?

In this article, product specialist Jeremy Winters says they do:
https://americanshootingjournal.com/precision-long-range-shooting-the-coriolis-effect/

 

[FatPhil]

The only 'effect' here would be a SWAT team showing up.....as guns are not allowed in the UK. Though hunting rifles must be allowed with special permits.....as when mountain climbing in Scotland I've a few times had to call the land owner to make sure deer hunting parties were not active.

Do snipers need to take the Coriolis effect into account ? I'm not sure. What I do know is that on a smaller scale of a kilometer or less the Coriolis effect is far less active. That is why in the northern hemisphere you get a few percent of tornadoes that rotate clockwise....opposite to the Coriolis effect. I would imagine that a sniper bullet would be travelling too fast for the Coriolis effect to have any significant impact....but its an intriguing question.

The UK is 0.04% of the planet, I'm not sure why you think it's important. I'm also curious which bit of the UK you think is at the equator.

And yes, snipers absolutely have to take the coriolis effect into account, at ranges much over a kilometer it makes a difference that can be measured in body widths. The planet is moving at a comparable speed to the muzzle velocity of a winchester 308 (about half) and the travel time is measured in seconds, it's significant.

 

[Mendel]

just like their challenges of finding water sticking to a sphere or gas pressure without a container and other examples that require a massive change of scale to demonstrate.

both have been demonstrated at small scales

Furthermore, they don't seem to be bothered with effects that have no plausible mechanism, such as the Sun and Moon orbiting in circles above the flat Earth with absolutely no mechanism explaining why they do that.

Isaac Newton didn't really know why, either.

 

[AmberRobot]

both have been demonstrated at small scales

Of course they have. Flat Earthers won't believe it anyway.

Isaac Newton didn't really know why, either.

Yes, but he made mathematical predictions that could be checked against reality. Any flat earther claim about the Sun's movement, position, and size is demonstrably false.

I won't hold my breath for any flat earth theory on par with Newton.

 

[FatPhil]

Yes, but he made mathematical predictions that could be checked against reality. Any flat earther claim about the Sun's movement, position, and size is demonstrably false.

"Why" is a metaphysical question. Newton was eventually happy that the law applied - the attraction he could measure was that law enacting between the particles he was measuring.

And in Newton's 1713 General Scholium in the second edition of Principia: "I have not yet been able to discover the cause of these properties of gravity from phenomena and I feign no hypotheses.... It is enough that gravity does really exist and acts according to the laws I have explained, and that it abundantly serves to account for all the motions of celestial bodies."[9]

https://en.wikipedia.org/wiki/Newton's_law_of_universal_gravitation

Chasing the "why"s or the "causes" is a somewhat futile endeavour, as each time you unravel another layer you need to ask what causes *that*. If you begin that process, you have the choice of saying it just goes on for ever - which implies that there are more layers to the laws of physics than there are particles in a finite universe for those laws to act upon, or to accept that one of the layers is justified by "that's just how it is". The former seems paradoxical, and the latter is your ticket to just saying, as Newton did in 1713, that Newton's Law of Universal Gravitation "is enough". And to that extent, from his own perspective, it's fair to say that he did "know why" as much as anyone knowadays does. (This being a reference to @Mendel's "Isaac Newton didn't really know why, either." in #117 upthread.) But that's just my personal opinion on a metaphysical matter (what is "really" anyway?). Well-reasoned disagreement is fine on such things.

 

[Mendel]

Yeah, that's basically the gist of it.
Science isn't superior because it explains "why" things happen, it's superior because it describes what happens in thorough detail (or tries to).

This is why globes are useful for navigation while FE maps do not exist.
It's why we can use geometry to predict sunrise times and solar eclipses while FE can't.
And why there are always counterexamples to FE claims.