Earth curvature refraction experiments - debunking flat/concave Earth

[Mick West]

????
No, in 'my' definition, the "bulge" height depends on the distance between the observer's horizon and the object behind the horizon. In this case, just the distance between the camera and the hull.

But you said:

the bulge is at the horizon

So that does not make sense with "bulge height", when the observer's height is zero (and hence anything "at the horizon" is coincident with the observer. Maybe you should draw a diagram, and indicate what you mean by "bulge height"?

 

[Trailspotter]

But you said:


So that does not make sense with "bulge height", when the observer's height is zero (and hence anything "at the horizon" is coincident with the observer. Maybe you should draw a diagram, and indicate what you mean by "bulge height"?

It wasn't me, who suggested the term, I've just used the @david Ridlen's term. By "bulge height", I mean the height of the part of the object behind the horizon that is hidden from view below the horizon.

In the above diagram, if the observer is at the top of the lighthouse, the "bulge height" is hB - the height of the boat (ship) mast. Respectively, if the observer is in the "crow nest" on the mast, the "bulge height" is hL - the height of the lighthouse. It the observer is in the point T with their eyes at the sea level, the "bulge heights" are again either hB, or hL, depending on the object of observation.

 

[Mick West]

By "bulge height", I mean the height of the part of the object behind the horizon that is hidden from view below the horizon.

Okay, but I think we should avoid the term, as it sounds more like it's referring to the height of the curvature of the Earth i.e. an actual bulge. Perhaps "obscured height" would be better?



The above should be interactive. Try moving the "Camera" and "Target" points

 

[Trailspotter]

Perhaps "obscured height" would be better?

I agree that "obscured height" is a better term. I think that actual "bulge" should refer to a water surface height above the mean curvature of the Earth surface/sea level, e.g., tidal bulge.

 

[Astro]

I believe you're correct on that. The guy who seems to be the source of this theory believes we should all humble ourselves to him because he is god.

I know there are rules against attacking individual people, but I felt it important to share this information for the sake of the safety of the posters here. The person Trigger Hippie is referring to, "Lord Steven Christ" or whatever he's calling himself this week, is a known stalker. He made threats against the owner of one of the major conspiracy websites and allegedly attempted to confront the owner in person at his home in Florida. Before that could happen he was arrested for other threats he made against President-elect Obama following the 2008 election.
http://www.huffingtonpost.com/2009/01/16/steven-joseph-christopher_n_158703.html
He was found guilty and sentenced to 3 years in prison starting in 2009. Obviously he has since been released.
http://www.clarionledger.com/article/20091106/NEWS/91106033/Man+who+threatened+Obama+sentenced
I say this just as a warning for anyone wishing to get involved in debunking this issue since Steven is the source of most of it. I initially started my own debunking before I was informed that this was the same Steven. I have personally decided that his history of death threats makes engaging the issue too dangerous. He already made one video about posts I made on another forum and I do not wish to draw any more attention from him. Again, I'm only presenting this so that others can also make an informed decision of how to approach it, or whether to approach it at all.

 

[David Ridlen]

Yes, "Earth bulge" and "obstruction/obscured height" should be separate terms, and are among several examples of confused perceptions I read in various Earth curvature discussions.

I am still wondering about the difference between the calculated 19' obstruction, and the seeming visual 14' obstruction in my comparison photos.

I dont understand equations at all, so I constructed a 3D scene to scale in order to observe actual dimensions. But is your obscured height derived from calculating the distance between observer and target as a straight line through the Earth, or as a circumferential arc around the Earth (like navigational 'great circle routes')?

The initial video experiments are referencing the Google Earth ruler which I assume represents a curved distance, not a straight line. Perhaps the difference is negligible at 6.58 mi, and the 5' difference may be due to variation in oblate bulge, as suggested. And perhaps the distance between the ferry and the camera is actually less than 6.58 mi, and/or the camera height is actually bit higher, or Google Earth may be slightly distorted somehow. And I have not found a clear way to calculate/guestimate refraction effects.

...What FE fans often calculate as the "bulge height" is actually the amount obscured if viewed from sea level...

FE'ers are usually referencing this simplified chart to predict the height of obstruction, using an exponential, 8" drop-per-mile rule http://www.sacred-texts.com/earth/za/za05.htm

"Lord Steven Christ" or whatever he's calling himself this week, is a known stalker. He made threats...

He is a special case. I have had ongoing discussion with Captain Christ(opher), and I do not fear that character who refers to himself as the "the greatest troll ever," but I recommend avoiding feeding his considerable ego with any attention.

 

[Mick West]

I am still wondering about the difference between the calculated 19' obstruction, and the seeming visual 14' obstruction in my comparison photos.

I think that's a combination of inaccurate estimation, variable waterline of the ferry (loaded/unloaded), and refraction. Given the variables I think 19 vs 14 is in the same ballpark. I don't think local difference in the shape of the earth is a factor. Wave swell possibly.

But is your obscured height derived from calculating the distance between observer and target as a straight line through the Earth, or as a circumferential arc around the Earth (like navigational 'great circle routes')?

The initial video experiments are referencing the Google Earth ruler which I assume represents a curved distance, not a straight line. Perhaps the difference is negligible at 6.58 mi,

The difference is negligible. Part of the problem here is that the Earth is so big, but diagrams are so small. It's hard to accurately show the magnitudes, so we get a false sense of the curvature. I've updated my little sim above to use an actual sized earth. Now, illustrations of the obscuration by the horizon are often shown like this:

But notice the huge sizes and distances we need to get a visible curve like that. The target is 252 miles high!! Here though the is a difference between the curved distance (2118 miles), and the "tunnel" distance (2092 miles).

But what about 6.58 miles? What does that actually look like? Really it's more like this:

Notice the curve distance and the straight line distance are the same, but that's just because the dispay use two decimal places. Really they are a few fractions of an inch different, but that does not make any significant difference to the end result.

Turning up the accuracy:

Curve = 6.58437499998, Straight = 6.5843742409 miles, a difference of less than 0.1 inches.

 

[Chew]

The distance to the horizon accounting for refraction is the square root of the height of eye * 1.345 statute miles.

If you know the height of the camera and the total distance you can calculate the other height of eye (i.e. how much is obscured).

Using the ferry example, the distance to the horizon from the camera is sqrt(1 ft)*1.345 mi = 1.345 mi.

Subtracting that distance from the total distance means the other height of eye is ((6.58 mi - 1.345 mi) / 1.345)² = 15.1 ft.

That is 4 feet less than Mick's trigonometric solution and closer to your guesstimate. Refraction accounts for the difference.

 

[Mick West]

The distance to the horizon accounting for refraction is the square root of the height of eye * 1.345 statute miles.

That value assumes a standard lapse rate - i.e. the density of the air decreasing at a constant rate, based on a standard atmosphere. At very low heights the density change could be very different - because of the heating or cooling effect of the ground or water, as noted here:

http://www-rohan.sdsu.edu/~aty/explain/thermal/std_atm.html

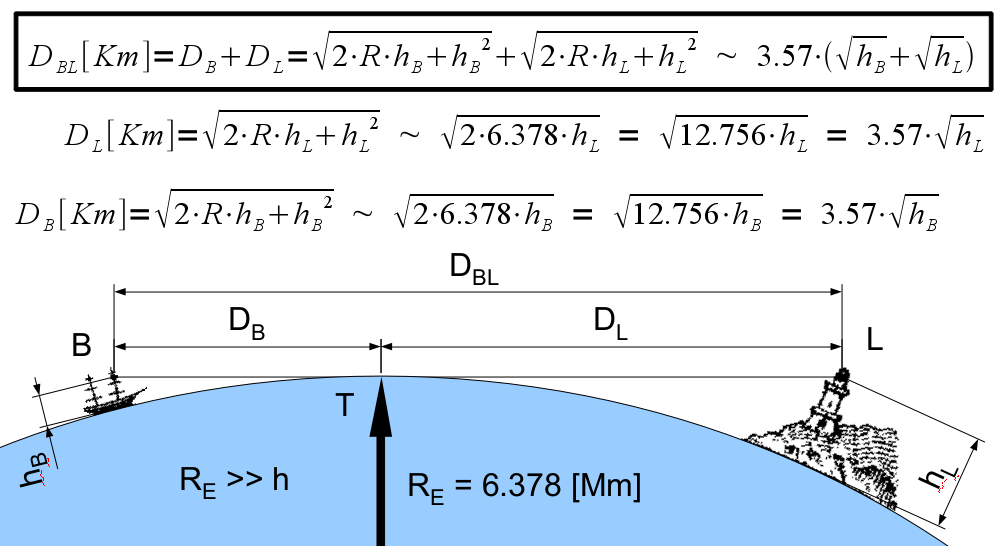
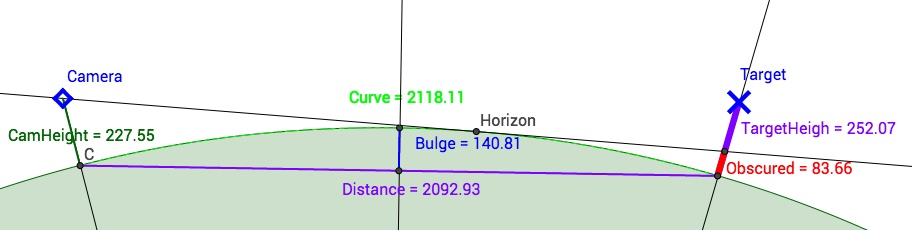
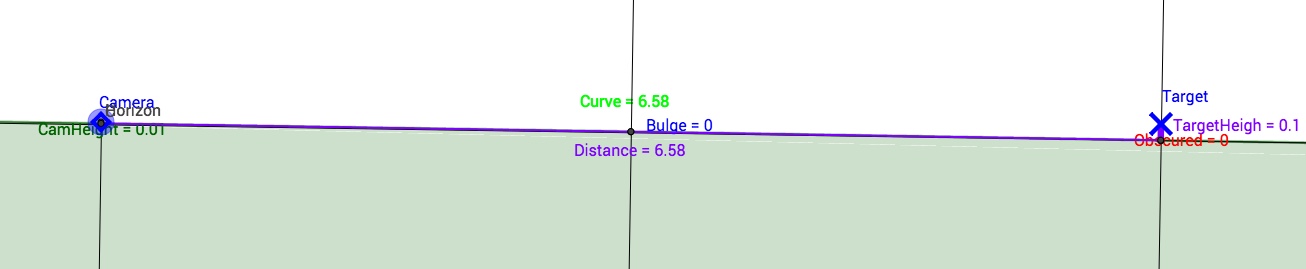
With a little digging, you can discover that the Standard Atmosphere can be traced back to 1920. The constant lapse rate of 6.5° per km in the troposphere was suggested by Prof. Toussaint, on the grounds that

… what is needed is … merely a law that can be conveniently applied and which is sufficiently in concordance with the means adhered to. By this method, corrections due to temperature will be as small as possible in calculations of airplane performance, and will be easy to calculate. …​

The deviation is of some slight importance only at altitudes below 1,000 meters, which altitudes are of little interest in aerial navigation. The simplicity of the formula largely compensates this inconvenience.

The above quotation is from the paper by Gregg (1920). The early motivations for this simplified model were evidently the calibration of aneroid altimeters for aircraft, and the construction of firing tables for long-range artillery, where air resistance is important.

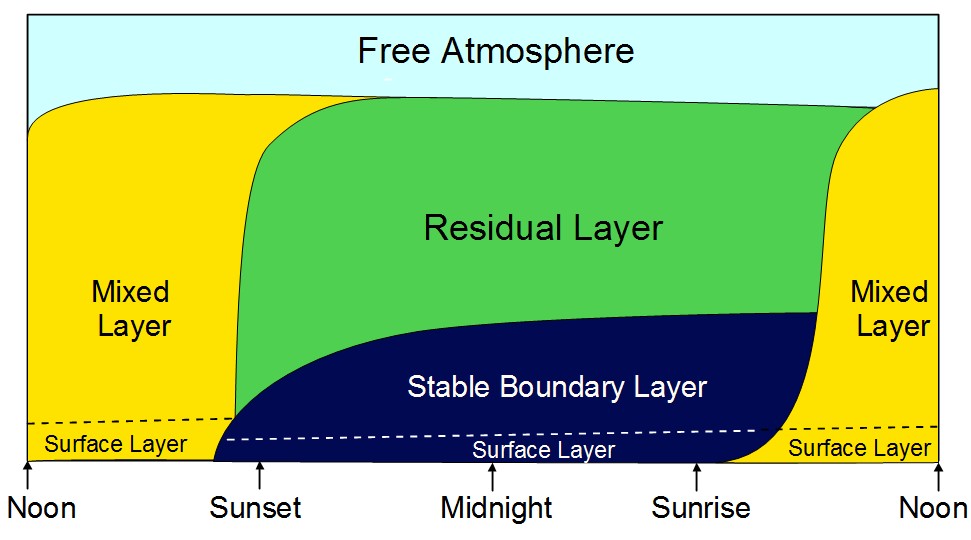
Unfortunately, it is precisely the inaccurate region below 1000 m that is most important for refraction near the horizon. However, the Toussaint lapse rate, which Gregg calls "arbitrary", is now embodied in so many altimeters that it cannot be altered: all revisions of the Standard Atmosphere have preserved it.

Therefore, the Standard Atmosphere is really inappropriate for astronomical refraction calculations. A more realistic model would include the diurnal changes in the boundary layer; but these are still so poorly understood that no satisfactory basis seems to exist for realistic refraction tables near the horizon.

"diurnal changes in the boundary layer" means the 24 hour cycle of temperature changes in the planetary boundary layer - i.e the layer of air next to the ground/water. Here's an illustration of how this varies over a day (the experiments in this thread take place in the "surface layer"):

source: http://elte.prompt.hu/sites/default/files/tananyagok/AtmosphericChemistry/ch01s05.html

Daly variation of PBL shows a typical pattern during pleasant weather condition (Fig 1.11.) The lowest (about 10%) part of PBL is called surface layer. The thickness of this layer is typically 10–30 m at night, and 50–100 m in day-time. Exchange processes between the atmosphere and the surface (vegetation) are realized here by the turbulent fluxes[17] of heat, momentum, water and air pollutants. After sunrise, a convective mixed layer growing rapidly due to the intensive turbulence. This layer is capped by a stable entrainment zone. Near sunset, the mixed layer collapses and in its place a nocturnal boundary layer is formed. The bottom part of this layer is stabilized by the nigh time radiative cooling of the surface. Above this stable zone a residual layer can be found.

Basically - there's a lot of variation, you can't actually calculate the value, just a range of possible values.

Here's a full derivation of the simple value.
http://mathscinotes.com/2013/08/distance-to-the-horizon-assuming-refraction/

 

[Pete Tar]

Does anyone have a good source to explain square roots in trigonometry - specifically, how to visualise their usefuleness and application, not just the 'rules' of using them?
(proofs I guess)

Edit: I found a few useful sites if any others are interested:
http://betterexplained.com/archives/
https://en.wikipedia.org/wiki/User:LucasVB/Gallery (maths gifs)
https://superplexa.wordpress.com/2010/02/11/why-are-square-roots-so-hard-to-learn/

 

[Mick West]

There's two uses of square roots here. One is just in finding the length of one side of a right angle triangle if you know two of the other sides. That's one of the most fundamental things in using trig practically.

Here's a nice visual proof of "the square of the hypotenuse is equal to the sum of the squares of the other two sides"


Then the other use is in solving quadratic equations. That's not really trig specific, just what arises here. It's simply an algorithm for solving an equation, you don't have to understand the proof, which is a bit tedious.

 

[guyonearth]

I know there are rules against attacking individual people, but I felt it important to share this information for the sake of the safety of the posters here. The person Trigger Hippie is referring to, "Lord Steven Christ" or whatever he's calling himself this week, is a known stalker. He made threats against the owner of one of the major conspiracy websites and allegedly attempted to confront the owner in person at his home in Florida. Before that could happen he was arrested for other threats he made against President-elect Obama following the 2008 election.
http://www.huffingtonpost.com/2009/01/16/steven-joseph-christopher_n_158703.html
He was found guilty and sentenced to 3 years in prison starting in 2009. Obviously he has since been released.
http://www.clarionledger.com/article/20091106/NEWS/91106033/Man+who+threatened+Obama+sentenced
I say this just as a warning for anyone wishing to get involved in debunking this issue since Steven is the source of most of it. I initially started my own debunking before I was informed that this was the same Steven. I have personally decided that his history of death threats makes engaging the issue too dangerous. He already made one video about posts I made on another forum and I do not wish to draw any more attention from him. Again, I'm only presenting this so that others can also make an informed decision of how to approach it, or whether to approach it at all.

This is highly interesting, as I have had a number of "discussions" with him on YouTube. He keeps wanting me to "skype" him so he can tell me more about the structure of his universe.

 

[Astro]

This is highly interesting, as I have had a number of "discussions" with him on YouTube. He keeps wanting me to "skype" him so he can tell me more about the structure of his universe.

Well personally I would be wary of granting him any access to personal information or anything he could even glean from a Skype chat, including your Skype account, but that's just me. Just be aware he has a history of violent threats and stalking.

 

[guyonearth]

Well personally I would be wary of granting him any access to personal information or anything he could even glean from a Skype chat, including your Skype account, but that's just me. Just be aware he has a history of violent threats and stalking.

Don't worry, I'm not that naive. I asked him how he enjoyed his three years in prison, he said he recommends it to everyone as a way to be more disciplined.

 

[TWCobra]

I've installed the "Theodolite" app on my iPad. Often with opposing traffic heading towards you, aircraft that are lower than your aircraft appear much higher than you when at a distance. It is an optical illusion caused by the curvature of the earth that only pilots get to see.

Next time I see it I will photograph it through the theodolite app. It should debunk the "flat-earth" once and for all.

 

[David Ridlen]

I've installed the "Theodolite" app on my iPad. Often with opposing traffic heading towards you, aircraft that are lower than your aircraft appear much higher than you when at a distance. It is an optical illusion caused by the curvature of the earth that only pilots get to see.

Next time I see it I will photograph it through the theodolite app. It should debunk the "flat-earth" once and for all.

Hmm... I dont follow. Sounds like proof of concave Earth.

 

[Mick West]

Hmm... I dont follow. Sounds like proof of concave Earth.

Think about what you have to do to "look at the horizon" in the case of flat, concave (bowl shaped), or convex (spherical) world.

(A) In a flat world, the horizon is directly ahead of you, very far away, you look essentially parallel to the ground.

(B) In a concave world, assuming there's an edge, then it's above you, you look up at it (relative to the ground)

(C) In a convex world (a globe), you look down to the horizon. Yet your brain is interpreting the scene as if the ground is flat. So it thinks you are looking parallel to some flat ground, and hence the other plane seems higher.

 

[TWCobra]

The photo I posted just shows the app; not what it looks like from the flight.

What it will show at 35000 feet when at 0 deg declination will be the horizon well below the zero line. That can only happen on a globe.

 

[Henk001]

Just to give an order of magnitude for the refraction effect. I've learned that when the sun starts setting (its lower edge hits the horizon) it is geometrically already below the horizon completely, because the angle of refraction for een object on the horizon is about 34 arcminutes, slightly more than the sun's apparent diameter.
Comparing this with the angle between the line of sight when you are looking at a height of 1,7 m at the horizon and the surface of the Earth -- about 2,7 arcminutes, the contribution of refraction can be expected to be substantual. I haven't tried to figure out what this quantitatively will be.

 

[David Ridlen]

What it will show at 35000 feet when at 0 deg declination will be the horizon well below the zero line. That can only happen on a globe.

That would be good evidence to reference. But I can already see Flat-Earthers will simplistically argue that the horizon is actually higher than it appears, and that it is just too far away to see in the haze, and/or due to perspective. "Perspective" is how they defend the Sun appearing to set below horizon, or why distant cities appear below sea level.

 

[Z.W. Wolf]

Hello;

Z.W. Wolf here. First post.

I ran across this YT video. I'm not strong in math so I wanted to check with you all to see if I've correctly spotted the fallacy.



-I agree that this the top 100 ft or so of the Duke Energy Center Tower in Charlotte, N.C.

https://www.google.com/search?q=duk...ved=0CAcQ_AUoAmoVChMIk4K0uPH_xgIVRM2ACh02-goZ

-I agree that the distance from where he is standing - The Edge of the World (a bluff near Edneyville, NC) - is about 80 linear miles from Charlotte.

Where he gets into trouble is here:

Charlotte, NC: 748 ft altitude
Duke Energy tower: 786 ft high
Combined altitude: 1,534 altitude

World's Edge : 2,880 ft altitude
That puts World's Edge 1,346 feet above the height of the top of the Duke Energy Tower. 80 miles away
there is 51,200 inches of drop, or 4,266 feet of drop from earth's supposed curvature.

That puts the top of the Duke Energy Tower about 2,920 ft below the supposed curvature of earth.

What he should have done is establish a virtual sea level (to coin a phrase) and then treat the tower and the bluff as two towers above that sea level. Then solve for the distance one could see the top of the tower from the top of the bluff.

To reduce Charlotte to that virtual sea level you should subtract 748 ft from its altitude of 748 ft to get it to zero. Then subtract 748 ft from the altitude of The World's Edge (2,880 ft):

2,880 ft - 748 ft = 2,132 ft.

Now we have the proper relationship of The World's Edge to Charlotte and can treat the World's Edge as a tower 2,132 ft above sea level.

Now we can treat the Duke Energy Tower as a tower 786 ft above sea level and solve using the method in this:

http://boatsafe.com/nauticalknowhow/distance.htm

The only problem with this site is that the measurements are in nautical miles. The formula for statute miles uses the factor 1.23 rather than 1.17.

https://en.wikipedia.org/wiki/Earth_bulge#Distance_to_horizon


My calculation goes like this:

Using the formula:

Distance in miles approximately equals 1.23 times the sqrt of height in feet

Height of World's End = 2,132 ft

Square root of 2132 = 46.1735855225
46.1735855225 x 1.23 = 56.7935101927 miles

This is the distance from the top of The World's End to the virtual sea level horizon.

Then we calculate the distance to the horizon from the top of the Duke Energy Center Tower

Height of Duke Energy Center Tower = 786 ft

sqrt of 786 = 28.0356915378
28.0356915378 x 1.23 = 34.4839005914 miles


Then we add the two together to see the maximum distance at which one could see the top of the Duke Energy Center Tower from the top of the World's End.

56.7935101927 miles + 34.4839005914 miles = 91.2774107841 miles


Now, I agree that we're only seeing the top 100 feet or so of the Duke Energy Center Tower so lets knock 100 feet off its total height.

786-100 = 686

sqrt of 686 = 26.1916017074
26.1916017074 x 1.23 = 32.2156701001 miles

Add that new figure to the figure for The World's End

56.7935101927 + 32.2156701001 = 89.0091802928 miles

89 miles. Well within the 80 miles distance he specified.

(I didn't round, but it's just as easy to cut and paste the whole figure, so what the hell)

Hope this is right.

 

[Z.W. Wolf]

Charlotte, NC: 748 ft altitude Duke Energy tower: 786 ft high
Combined altitude: 1,534 altitude

World's Edge : 2,880 ft altitude
That puts World's Edge 1,346 feet above the height of the top of the Duke Energy Tower. 80 miles away
there is 51,200 inches of drop, or 4,266 feet of drop from earth's supposed curvature.

That puts the top of the Duke Energy Tower about 2,920 ft below the supposed curvature of earth.



I don't know what formula he's using to get the "drop." But if you use the formula

d in miles = 1.23 x sqrt of height in feet

and use it to solve for height

d in miles divided by 1.23 = sqrt of height in feet

80/1.23 = 65.04

65.04 squared = 4,230.29 feet

Which is pretty close to his figure of 4,266 feet


He gets into trouble when he subtracts the altitude of Charlotte plus the height of the Duke Energy Center Tower from the altitude of The Edge of the World. I think you should add all of these figures together.

748 + 786 + 2,880 = 4,414 feet.

Which puts the top of the tower 148 feet above his drop of 4,266 feet.

But I'm having a hard time putting into words why you should do this; in a way he could actually picture it. I'm not sure I'm picturing it correctly.

But the formula is for zero feet altitude to zero feet altitude (sea level to sea level) The bluff and the top of the tower are both above sea level so you have to add the altitudes together.

I'm picturing a perfect circle with two bumps on the surface. You have to calculate the drop on the perfect circle. And then see if the drop is greater or lesser than the combined altitude of the two bumps.

I'm not sure about this. I'd appreciate any corrections or comments.

 

[Z.W. Wolf]

To prove that there's something screwy about his calculations.


Charlotte, NC: 748 ft altitude Duke Energy tower: 786 ft high
Combined altitude: 1,534 altitude

World's Edge : 2,880 ft altitude
That puts World's Edge 1,346 feet above the height of the top of the Duke Energy Tower. 80 miles away
there is 51,200 inches of drop, or 4,266 feet of drop from earth's supposed curvature.

That puts the top of the Duke Energy Tower about 2,920 ft below the supposed curvature of earth.

Subtract the altitude of the tower from the altitude of The World's End

2,880 ft - 1,534 ft = 1,356 ft

Subtract that figure from the drop due to the supposed curvature of the Earth.

4,266 ft - 1,356 ft = 2,920 ft

And the top of the tower is 2,920 ft below the supposed curvature of the Earth.

But if by the same logic you subtract the altitude of Charlotte from the altitude of The World's End

2,880 ft - 748 ft = 2,132 ft.

Subtract that from the drop

4,266 ft - 2132 = 2,134

And the altitude of Charlotte is 2,134 ft below the supposed curvature of the Earth.... compared to the tower's 2,920 ft below the supposed curvature.

Which means that Charlotte is 786 fewer feet below the supposed curvature of the Earth than the top of tower is. Which means if you took off in an airplane from the top of The World's End, maintained the altitude of 2,880 feet and traveled toward Charlotte on the supposed ball Earth... you would see the base of the tower before you would see the top of the tower.


Finally, if the top of the tower was 1,346 below sea level it would be at exactly the right height to be seen from The World's End

2,880 ft - (-1,386 ft) = 4,266 ft

4,266 ft - 4,266 ft = 0 ft below the supposed curvature of the Earth.

There's something screwy going on here.

 

[Chew]

I don't know what formula he's using to get the "drop."

The formula the flat earthers usually use (always use?) is statute miles² x 8 inches = drop in inches.

The part the FE messed up is the 4266 foot drop only applies if your height of eye is 0 feet. Their formula uses squares (²) and if you break up the total drop for different heights of eye and add up the drops you will not get a total drop of 4266 feet except when one of the heights of eye is 0 feet.

For example, at 27.38 miles the first drop is 500 feet. To make up the remaining 80 miles (a difference of 52.62 miles) means the second drop will be 1846 feet. Add the two drops (500 feet and 1846 feet) and you get a total drop of 2346 feet.

Other examples for a distance of 80 statute miles with various heights:
100 feet and 3060 feet = 3160 feet total drop
200 feet and 2619 feet = 2819 feet total drop
1000 feet and 1135 feet = 2135 feet total drop
2132 feet and 366 feet = 2498 feet total drop

 

[mrfintoil]

Is it just me or is Flat Earth theories trending within the conspiracy community right now? I keep seeing them being mentioned more and more frequent. According to Google Trends, "Flat Earth" is trending on their search engine.

 

[Z.W. Wolf]

Exploding.

 

[Pete Tar]

That is bit odd given that one of the fall-back responses from conspiracy-prone types to criticism of any new psuedo-science is "Well scientists used to the think the earth was flat".

 

[Chew]

Is it just me or is Flat Earth theories trending within the conspiracy community right now?

I'm seeing it more and more too. Used to be calling someone a flat earth believer was an insult but nowadays more and more of them seem to embrace the moniker. It's kinda surprising it took so long for so many CTers to be swayed by the flat earth theory given their previous inability to separate science from nonsense.

 

[mrfintoil]

Might be due to the increased media focus on recent space endeavours. So when big brother (ie. the government) tells us something about space, it must be wrong. Because... You know... The government and stuff.

Perhaps the fading out media focus on the war on terror also have effects on the conspiracy community. Google trends shows both "9/11 truth" and "war on terror" in a steady decrease. And you don't see so much "war on terror" stuff on TV any more.

Just a theory.

 

[Z.W. Wolf]

I think a big reason is because to be leader in the community you have to be more radical than the followers. It's a Red Queen's race, though; because someone else will just go onto something more radical. And if you just stand still, you get left behind in a formerly radical idea that becomes mundane established reality.

The Moon used to be very real place and it was only the Apollo Landings that were fake. Now the Moon is fake. That's the new thing coming on strong behind the Flat Earth.

This guy is a leading light in the Fake Moon movement

https://www.youtube.com/user/Crrow777

Gone are the naïve days when we had simple JFK assassination theories. Now the Moon is fake. All science is fake. There are no satellites - all fake. NASA is an evil Masonic/Satanic organization that feeds the sheeple disinformation from birth. There's talk that we live in a fake, controlled reality.

We're talking about fantasy prone people with poor reality testing in the first place; so to them anything on the vulnerable edge of the weird frontier seems intriguing rather than incredible. The Moon is fake? Tell me more!

And the Internet has sped all this up to a frenetic pace. It used to be a few guys who would write a new book every few years. There were scattered readers here and there across the world, with little contact. Now it's thousands of guys making new YT videos every few days, and legions of true believers spending all day sucking it up and writing comments.

 

[solrey]

To me all this flat Earth fake moon NASA always lies nonsense is just mental laziness. Science is hard, making stuff up is easy.

 

[Mick West]

Is it just me or is Flat Earth theories trending within the conspiracy community right now? I keep seeing them being mentioned more and more frequent. According to Google Trends, "Flat Earth" is trending on their search engine.

I think this is in part because recreational debunkers enjoy debunking the stilly logic and math. Many of the flat earthers are just trolling, and so they post more when people respond to them, which affects the true believers. I think if they were just ignored, the theory would be less popular.

 

[Z.W. Wolf]

This is a follow-up to what I wrote about this...



This is a video taken from a bluff or escarpment called The World's Edge, near the town of Edneyville, NC. You can see the top of the tallest tower in Charlotte about 80 miles away.

We have to look at the elevations along the line of sight between The World's Edge and Charlotte. If there were no hills or ridges between The World's Edge and Charlotte, and if the world were flat, we would see all of Charlotte. He is implying that there is a ridge which is blocking the view, and just allowing the Duke Energy Center tower to peek over that elevation.


But what is the line of sight between those two points? We can ignore all the closer ridges and hills we can see, because obviously they are not blocking our line of sight. It's that last ridge that we have to look at. The compass heading from The World's Edge to Charlotte is 97 degrees; 7 degrees south of east. The line of sight passes over Gastonia, NC. - (we can see the ridge get higher toward King's Mountain on our right). This is the last high elevation to the west of Charlotte. On the east side of this ridge is a low area around the Catawba River. Charlotte is 20 miles east of the ridge and is slightly higher than the river and its lakes.


That last ridge around Gastonia is 20 miles west of Charlotte and is about 850 feet above sea level. Charlotte is 748 feet above sea level. Which means that ridge is only 102 feet higher than Charlotte. And 682 feet lower than the top of the Duke Energy Center tower.


If the world is flat, why can't we see the rest of Charlotte?


The World's Edge is 2,880 feet high, and the last ridge is 850 feet high and is 20 miles west of Charlotte. Which by the laws of perspective on a flat Earth would hide virtually none of Charlotte from that high 2,880 foot escarpment. Because it is 20 miles west it would hide less of Charlotte than if it were only 10 miles or 5 to the east. Which can be easily proved.


If he wants to argue that the last ridge we see is a much higher ridge that's closer to the camera and is hiding the area around Gastonia... Where is that ridge; which is high enough to do that? If it were closer to the camera it would have to be much higher than the ridge on which Gastonia sits, and the closer it was to the camera, the higher it would have to be. Where is that tall ridge along the line of sight between The World's Edge and Charlotte? There is none on the map.

You also have to look at the video and count the towns (water towers) and ridges that we can see. We're seeing a long, long way to that last ridge. The theoretical ridge has to be in between those ridges and towns and the ridge on which Gastonia sits. Where is it?

Another problem he runs into is that the video disproves a theory he's pushing on another of his YT videos.



This is a common fallacy: that a boat goes hull down because of perspective and if you just use "more zoom" you can make the missing part of the hull re-appear. But at all levels of zoom he uses, no more or less of the tower is visible above the ridge.


This video proves that the Earth is not flat and disproves this perspective fallacy.

 

[Chew]

@Z.W. Wolf, both formulas are correct; he just misapplied his.

 

[Z.W. Wolf]

The formula the flat earthers usually use (always use?) is statute miles² x 8 inches = drop in inches.

The part the FE messed up is the 4266 foot drop only applies if your height of eye is 0 feet. Their formula uses squares (²) and if you break up the total drop for different heights of eye and add up the drops you will not get a total drop of 4266 feet except when one of the heights of eye is 0 feet.

For example, at 27.38 miles the first drop is 500 feet. To make up the remaining 80 miles (a difference of 52.62 miles) means the second drop will be 1846 feet. Add the two drops (500 feet and 1846 feet) and you get a total drop of 2346 feet.

Other examples for a distance of 80 statute miles with various heights:
100 feet and 3060 feet = 3160 feet total drop
200 feet and 2619 feet = 2819 feet total drop
1000 feet and 1135 feet = 2135 feet total drop
2132 feet and 366 feet = 2498 feet total drop

I'm now seeing that my method was as naïve as his. They both depend on the eye or camera being at zero feet. And the reason my method seemed to work out was complete coincidence. It's the intervening landscape that is obscuring most of the tower and the rest of Charlotte for that matter. Using the math presented here on this site, if Charlotte were at sea level and on the shore of an island, and the escarpment - which is 2,880 feet high - were on a mountain of another island, only 130 feet of Charlotte would be obscured and we would be able to see everything above that. But since Charlotte is at 748 feet above sea level, we would see all of Charlotte if we were looking across the sea and it were built on an island mountain.

I also made a mistake in establishing that "virtual sea level" by subtracting the sea level height of Charlotte from the sea level height of the escarpment. That is not valid. All you have to do is find the distance to the horizon for both Charlotte and the escarpment and add them together. That figure is 99.64 miles, and downtown Charlotte is only 80 miles from the escarpment. Which confirms that Charlotte would be completely visible across a body of water.

 

[Chew]

I also made a mistake in establishing that "virtual sea level" by subtracting the sea level height of Charlotte from the sea level height of the escarpment.

Huh? That wasn't a mistake. That was the correct way to calculate the drops and horizon distances. Subtracting 748 feet to get a 'virtual sea level' won't appreciably change the math given the 20.9 million foot radius of the Earth.

 

[Z.W. Wolf]

Hmmm. I'll have to figure this out. At the least, I don't think it was necessary.

Sorry for the deleted posts. I'm still getting used to this MB.

 

[Z.W. Wolf]

@Z.W. Wolf, both formulas are correct; he just misapplied his.

Right. I should say that I misapplied my formula as naively as he did. I'm learning, which makes this a great place.

 

[Mick West]

Right. I should say that I misapplied my formula as naively as he did. I'm learning, which makes this a great place.

A general problem here seems to be doing geometry with words rather than pictures. In his famous book "How to Solve it", G. Polya offers a four step heuristic for solving mathematical problems. The most memorable and useful part of this for me is in step one "Draw a figure, introduce suitable notation".

This has been my problem solving method for 30 years. Draw a figure, introduce suitable notation (i.e. label the known, unknown and intermediate quantities, lengths, angles, vectors, etc. with letters, so you can use algebra), then solve for the unknown.

The figure does not need to be impressive. Here I just draw it on a notepad, and took a photo of it with my phone:

 

[Trailblazer]

The formula the flat earthers usually use (always use?) is statute miles² x 8 inches = drop in inches.

The part the FE messed up is the 4266 foot drop only applies if your height of eye is 0 feet. Their formula uses squares (²) and if you break up the total drop for different heights of eye and add up the drops you will not get a total drop of 4266 feet except when one of the heights of eye is 0 feet.

That error reminds me of an Apollo hoaxer trying to use absolute speeds rather than velocity changes in the formula E = ½mv2​ to try and convince me that the lunar module rocket could not have carried enough fuel to perform the necessary accelerations.

A conspiracy-oriented mindset combined with a shaky grasp of maths is a dangerous thing