I have a technical question to ask you all
In SpaceEngine, https://spaceengine.org/ ( what a great piece of software it is ), if you try to land on a planet ( say planet Earth ), and look at the horizon, you will see that the horizon is basically flat.
Let's say we turn off the clouds and atmosphere, to leave only the ground and water visible;
we will place our point of view on a ground practically at water level, and without hindrance all around (in the sense of placing it as if we were observing the horizon practically from the surface of the water );
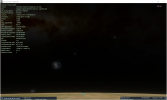
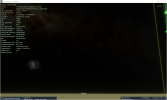
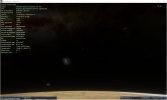
if I then try to raise My observation point to 5km( 3.106856 mile ) above the ground, I will notice that a slight curvature on the sides of the horizon is already beginning to be seen; the higher I go, the more and more such curvature becomes visible, on both sides of My point of view ( as well as a slight bump in the center );
what I wonder, and I ask you all, is whether the SpaceEngine graphics engine produces some kind of image deformation, which could account for the curvature that one begins to see at the horizon already from 5km( 3.106856 mile ) height from the ground.
I thought that on the globe ( oblate ellipsoid ) the curvature at the horizon would begin to be seen from heights much greater than only 5km( 3.106856 mile );
if the SpaceEngine 3D engine does not produce any image deformation, on the sides of the screen, does it mean that the Earth's atmosphere is solely responsible for our not being able to see, in reality, the earth's curvature from such low heights ?
Or is there someone who claims that the Earth's curvature is visible, in reality, even from 5km( 3.106856 mile ) above the ground ?
I think it's just the Earth's atmosphere, the optical phenomena within it , the factor that should prevent you from seeing the curvature from such low heights, as instead you can see in SpaceEngine, by turning off the atmosphere, right ?
The field of view of one's point of view I don't think it has anything to do with it, in this, because if if I am observing a sphere, at the horizon ( so My point of view is on the sphere, at varying heights above the ground ), I will ALWAYS see, on the sides of My point of view, curvature, as well as a bump in the center of it; if the sphere is monstrously gigantic, it would require a greater height from the ground, to be able to begin to see these things, it is true; but here I refer to the dimensions of the planet Earth, and their supposedly mathematically correct representation in SpaceEngine, where, even at heights of 3-5km above the ground, without( switch off ) the atmosphere, the curvature on the sides can be seen well, distinctly.
The field of view in SpaceEngine can be modified ( and it behaves like a sort of linear zoom, compared to what you see; behaves correctly, this, I'm saying ) : if I set it as that of human sight ( and i think it is the default value ), there should therefore be no correspondence problems, between the hypothetical reality (the one where I get up from the ground at a height of 3-5km, 'turn off' the atmosphere, and I observe the horizon ), and the simulated reality inside SpaceEngine( where I do the same thing )
( All the above, is, you think ) correct ?
Thank you
In SpaceEngine, https://spaceengine.org/ ( what a great piece of software it is ), if you try to land on a planet ( say planet Earth ), and look at the horizon, you will see that the horizon is basically flat.
Let's say we turn off the clouds and atmosphere, to leave only the ground and water visible;
we will place our point of view on a ground practically at water level, and without hindrance all around (in the sense of placing it as if we were observing the horizon practically from the surface of the water );
if I then try to raise My observation point to 5km( 3.106856 mile ) above the ground, I will notice that a slight curvature on the sides of the horizon is already beginning to be seen; the higher I go, the more and more such curvature becomes visible, on both sides of My point of view ( as well as a slight bump in the center );
what I wonder, and I ask you all, is whether the SpaceEngine graphics engine produces some kind of image deformation, which could account for the curvature that one begins to see at the horizon already from 5km( 3.106856 mile ) height from the ground.
I thought that on the globe ( oblate ellipsoid ) the curvature at the horizon would begin to be seen from heights much greater than only 5km( 3.106856 mile );
if the SpaceEngine 3D engine does not produce any image deformation, on the sides of the screen, does it mean that the Earth's atmosphere is solely responsible for our not being able to see, in reality, the earth's curvature from such low heights ?
Or is there someone who claims that the Earth's curvature is visible, in reality, even from 5km( 3.106856 mile ) above the ground ?
I think it's just the Earth's atmosphere, the optical phenomena within it , the factor that should prevent you from seeing the curvature from such low heights, as instead you can see in SpaceEngine, by turning off the atmosphere, right ?
The field of view of one's point of view I don't think it has anything to do with it, in this, because if if I am observing a sphere, at the horizon ( so My point of view is on the sphere, at varying heights above the ground ), I will ALWAYS see, on the sides of My point of view, curvature, as well as a bump in the center of it; if the sphere is monstrously gigantic, it would require a greater height from the ground, to be able to begin to see these things, it is true; but here I refer to the dimensions of the planet Earth, and their supposedly mathematically correct representation in SpaceEngine, where, even at heights of 3-5km above the ground, without( switch off ) the atmosphere, the curvature on the sides can be seen well, distinctly.
The field of view in SpaceEngine can be modified ( and it behaves like a sort of linear zoom, compared to what you see; behaves correctly, this, I'm saying ) : if I set it as that of human sight ( and i think it is the default value ), there should therefore be no correspondence problems, between the hypothetical reality (the one where I get up from the ground at a height of 3-5km, 'turn off' the atmosphere, and I observe the horizon ), and the simulated reality inside SpaceEngine( where I do the same thing )
( All the above, is, you think ) correct ?
Thank you