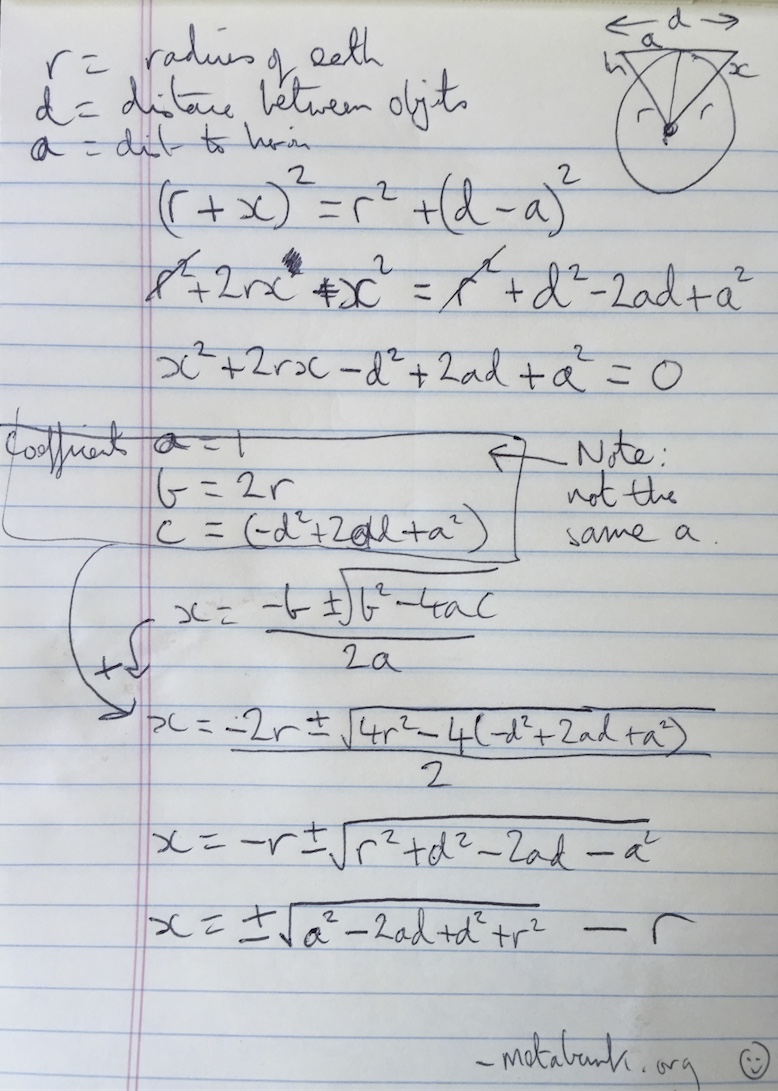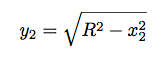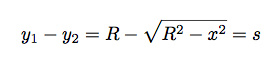Earth curvature refraction experiments - debunking flat/concave Earth

[David Ridlen]

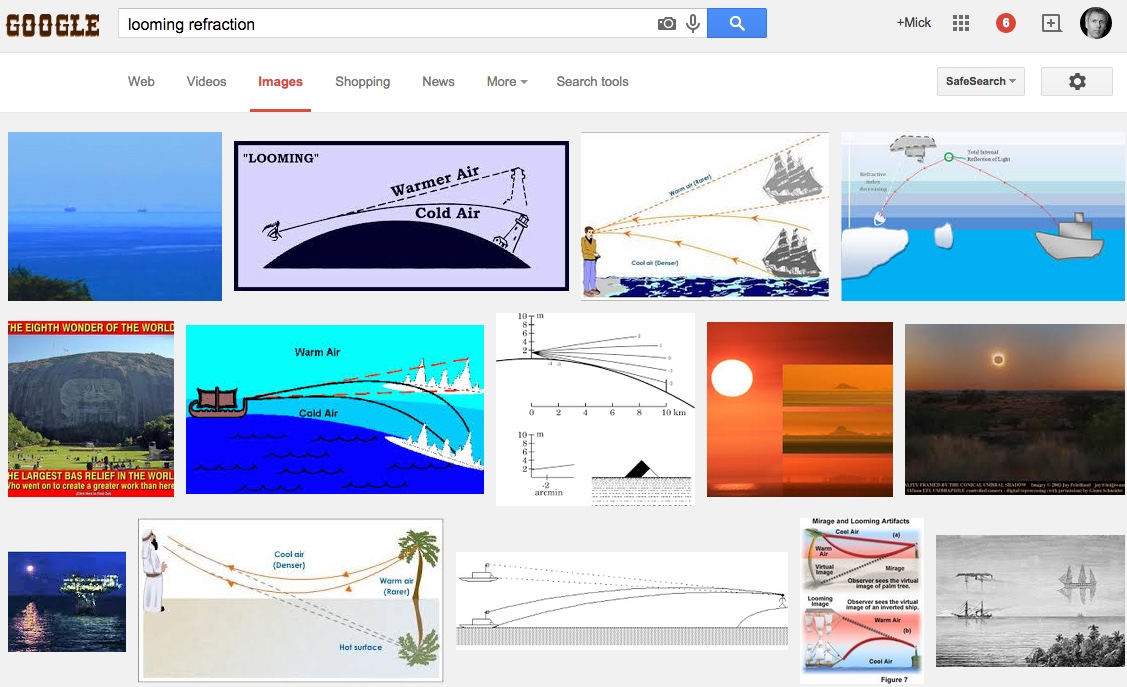
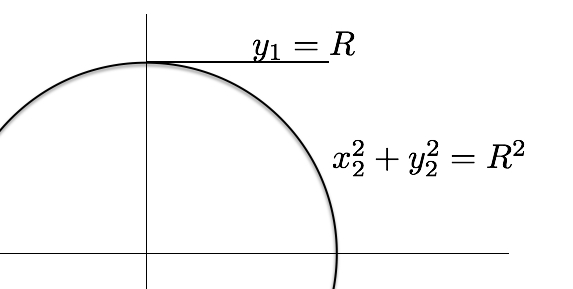
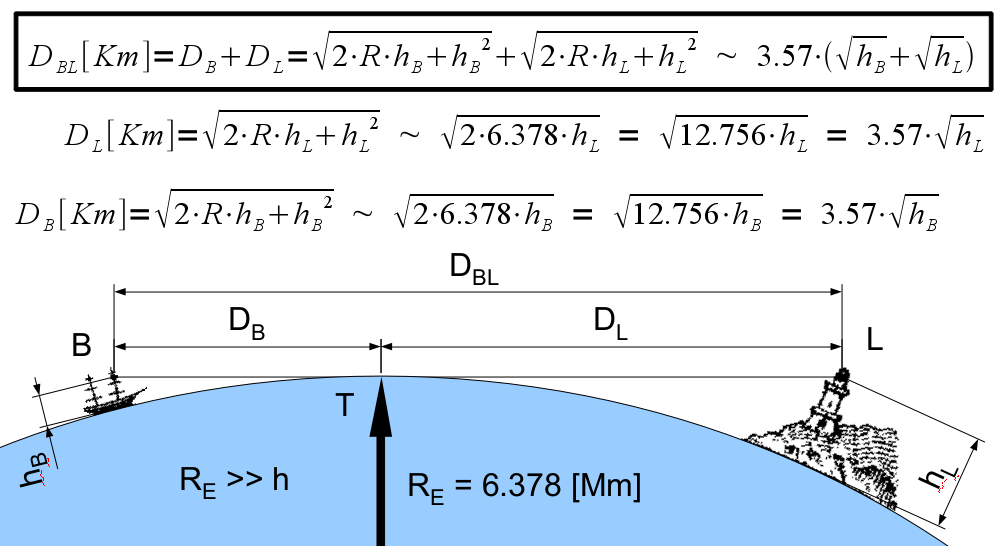
I keep being presented with 'earth curvature experiment' videos recently, by flat/concave earth advocates. It seems to be their new favorite "evidence" that Earth is not spherical. Debunking this gets into math which I stink at, regarding refraction. I would like to be sure I have considered all the factors. And I keep looking for a simple rule of thumb, like 'for each mile, the line of sight drops X amount, due to refraction' value.

So for example, this '20 mile laser' experiment comes up-
Source: https://www.youtube.com/watch?v=b8bpPTsPgsU

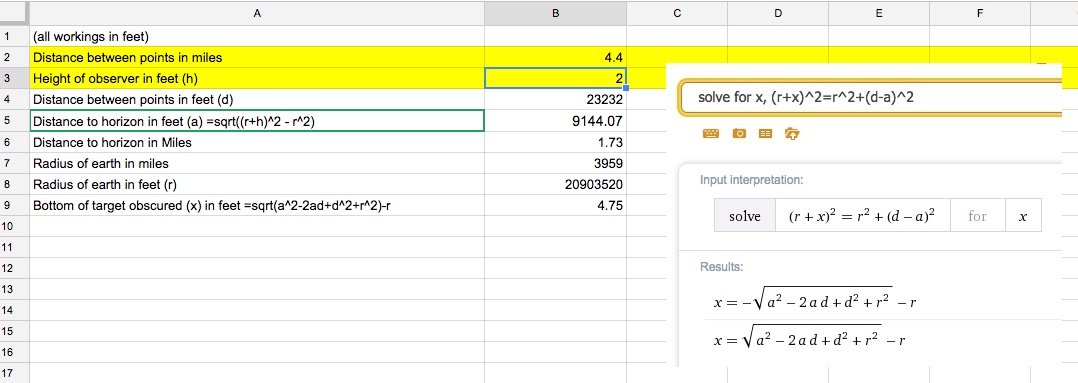
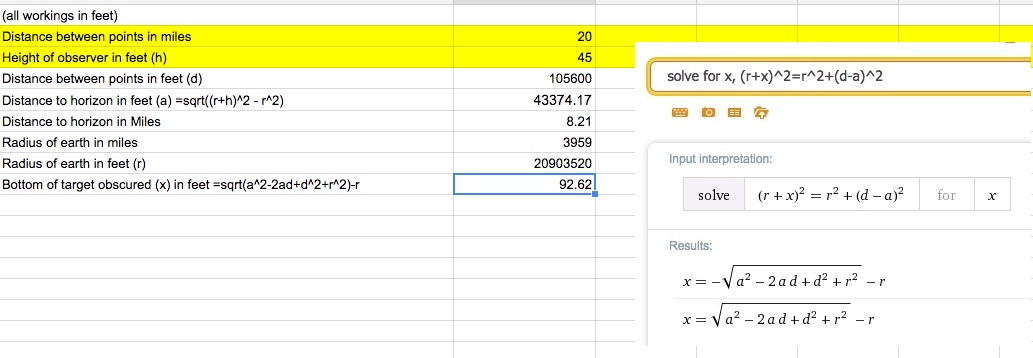
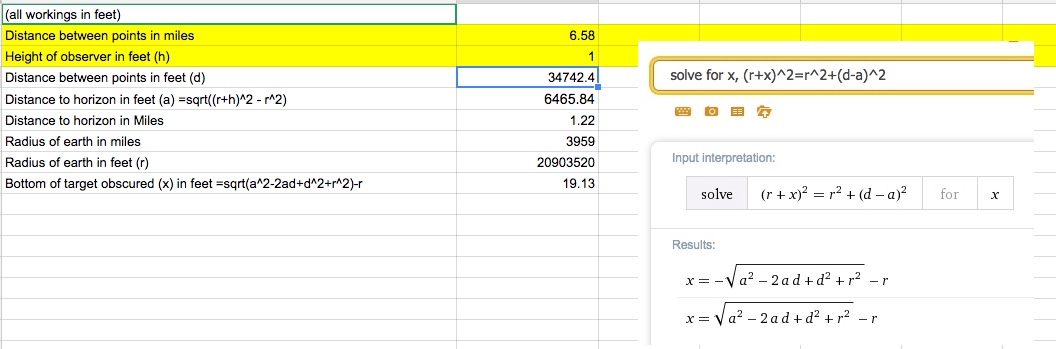
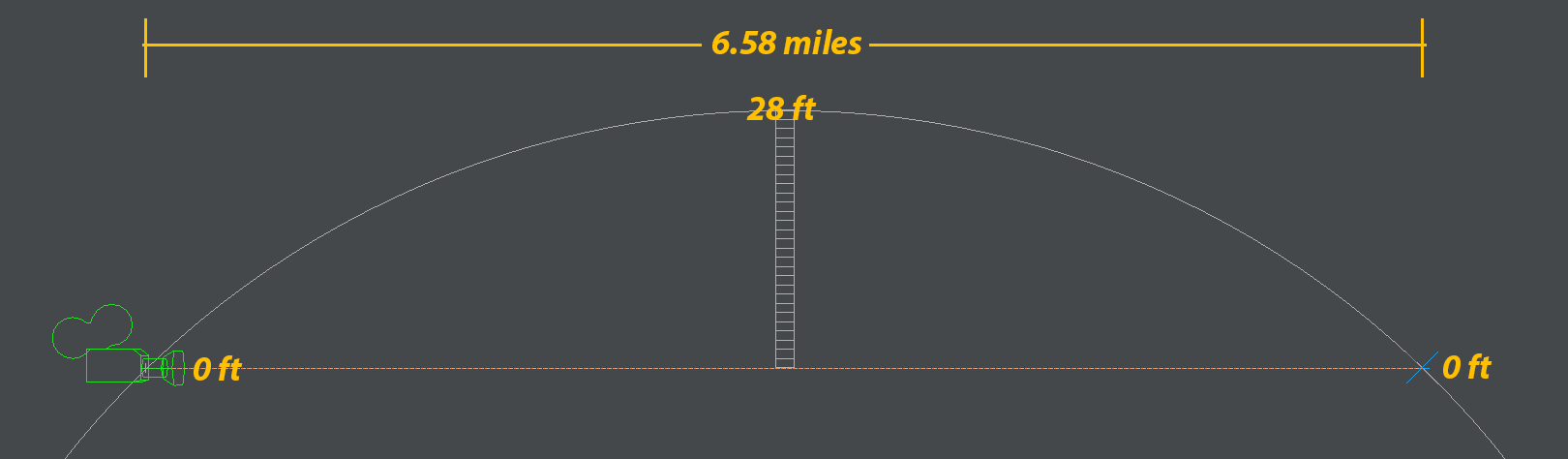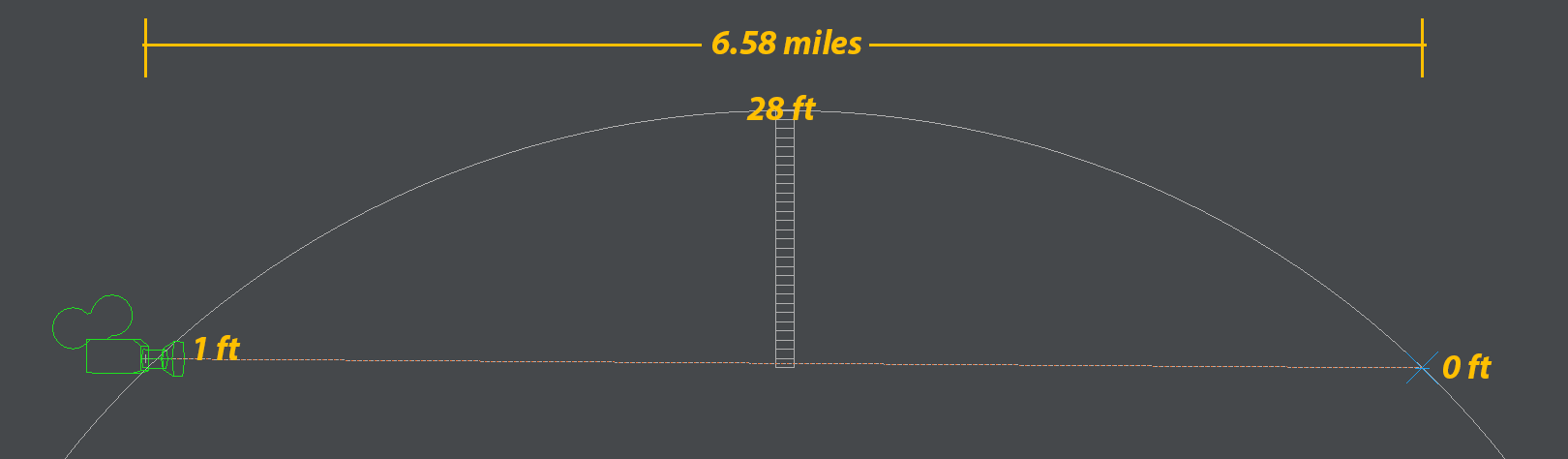
that claims to defy limitations of Earth curvature. It is sloppy, but assuming they are not cheating, the laser's horizontal line of sight is 65 feet above sea level, so does it make sense to be able to see a laser from 20 miles away, over water, at a height of 65 feet above sea level when the geographic (actual) line of sight would prevent the laser from traveling more than 10 miles over the Earth's curved surface? Does atmospheric refraction normally account for the laser distance doubling? And how to explain why it does make sense, in simplest terms?

I am also wondering if the laser could be "skipping" over the surface, kinda like a skipping rock over water, but in a few, long arcs. So the laser might graze the water surface near sea level peak/bulge at around 10 miles, then is reflected back upward, and arcs over the 'hump' another ten miles, or more, due to refraction. Thus the laser covers more distance than if it were traveling over level ground that is non-reflective.

Sites explaining refraction calculation are too mathy for my simple right-brain (figuratively speaking). And I seem to be reading conflicting rules, and I am interpreting different end results. I understand there are several refraction variables, like altitude, temperature, pressure, and moisture, and I understand that the closer to the water, and the greater the distance, the more the laser will refract, or 'super refract.' But I learned from a "Curvature and Refraction" video regarding geodetic surveys, that surveyers use a standard 7% rule-
But subtracting 7% does not seem to account for the laser traveling twice the distance over the curved Earth, as in the 20 mile laser example.

The WikiP entry on "Horizon- effects of refraction" http://en.wikipedia.org/wiki/Horizon#Effect_of_atmospheric_refraction- says something about using a 4/3 ratio, and 15% beyond geometrical horizon. And 'standard' atmospheric refraction is 8%, although that is not 'super' refraction as I assume would apply to the laser example. But these values do not match the 7% rule, and I dont get how all the values are applied to get a definitive refraction value.

I see a simple 'Distance to horizon calculator' here http://www.ringbell.co.uk/info/hdist.htm but it does not figure in refraction.
Another site, "Calculating Altitudes of Distant Objects" http://www-rohan.sdsu.edu/~aty/explain/atmos_refr/altitudes.html has a calculator to determine refraction 'lapse rate' , but no matter what I enter for the values, the lapse rate always comes out "0." It doesnt seem to work.

Any clarification is much appreciated.

 

[Chew]

The math in the video is correct but it doesn't matter because the video debunks itself. If the Earth were concave then the laser light would appear higher above the horizon the farther away it is.

 

[Soulfly]

http://www.howitworksdaily.com/how-high-do-you-have-to-go-to-see-the-curvature-of-the-earth/

However, you can detect the curve of the Earth from ground level at the coast with a pair of binoculars – just look for distant ships on the horizon and you'll see that their hulls start to disappear before their masts and other superstructure. Ancient Greek scientists, who spotted this without any optical aids, used this to conclude that the Earth was round.

 

[Tycho's Nose]

It could be the result of a superior mirage. Temperature inversions are common in the area (Suisun Bay, California), and a beam of light entering the inversion from below will be refracted back downward, effectively "skipping" over a greater distance as you suggest. From the target, the source light will appear to be higher than it actually is.

 

[David Ridlen]

Thanks all!

" If the Earth were concave then the laser light would appear higher above the horizon the farther away it is."

It sounds like you are actually confirming what concave advocates claim- 'the laser light would appear higher above the horizon in a concave Earth.'

" you can detect the curve of the Earth from ground level at the coast with a pair of binoculars – just look for distant ships on the horizon"

That is going into different evidence, which I have already covered. I would like to specifically address the laser experiments.

But I have already posted a debunk video showing a sailing ship disappearing hull-first over the horizon with my Flat Earth Debunk SLAMDUNK vid- among several other 'round Earth' observations.

And as you suggested, I also showed how curvature is observable with any zoom lens, showing Toronto below sea level from across Lake Ontario-


But if I can debunk 99% of the flat/concave "evidence," that wont be good enough if there is one thing, like the laser experiment that I cant adequately debunk, then that alone proves to them that there is a vast global space conspiracy of 50 years.

 

[Chew]

It sounds like you are actually confirming what concave advocates claim- 'the laser light would appear higher above the horizon in a concave Earth.'

Confirming? I'm not confirming it. I'm saying that is what would happen if the Earth were convex. Tell those yahoos to back up another 20 miles and try it again. If they can see the laser at that distance then they'd have a case.

 

[Mick West]

Looming seems the simplest explanation.

http://en.wikipedia.org/wiki/Looming_and_similar_refraction_phenomena

Looming is the most noticeable and most often observed of these phenomena. It is an abnormally large refraction of the object that increases the apparent elevation of the distant objects and sometimes allows an observer to see objects that are located below the horizon under normal conditions.

Also possible is reflection of the bottom of the bridge. Which looks to be around 60 feet high at that point.

 

[Trailblazer]

Confirming? I'm not confirming it. I'm saying that is what would happen if the Earth were convex. Tell those yahoos to back up another 20 miles and try it again. If they can see the laser at that distance then they'd have a case.

Or more to the point, why is there a "horizon" at all, if the Earth's is concave? Surely the ground/ocean should just appear to rise and gradually get fainter and fainter the higher up you look, due to atmospheric extinction? There would be no sharp cut-off.

 

[Trigger Hippie]

But if I can debunk 99% of the flat/concave "evidence," that wont be good enough...

I believe you're correct on that. The guy who seems to be the source of this theory believes we should all humble ourselves to him because he is god.

As for debunking the video, I think it debunks itself. I don't see a "direct hit" from the blue laser. The camera appears to capture a faint blue glow whose source is over the horizon. A little like the image below, the laser is visible but the source is obscured by trees.

 

[Hevach]

Or more to the point, why is there a "horizon" at all, if the Earth's is concave? Surely the ground/ocean should just appear to rise and gradually get fainter and fainter the higher up you look, due to atmospheric extinction? There would be no sharp cut-off.

Depends on the inner diameter. I can't for the life of me actually find a labeled diagram of what this concave earth is supposed to look like. Is this like some kind of miniature Dyson Shell, or is it a bowl-shaped version of the old "turtles all the way down" flat earth?

 

[Trailspotter]

Depends on the inner diameter. I can't for the life of me actually find a labeled diagram of what this concave earth is supposed to look like. Is this like some kind of miniature Dyson Shell, or is it a bowl-shaped version of the old "turtles all the way down" flat earth?

Like this?
http://en.wikipedia.org/wiki/Hollow_Earth#Concave_hollow_Earths

An example of a concave hollow Earth. Humans live on the interior, with the universe in the center.

Abdelkader devised an equation that suggests the phenomena belonging to the perception of the sky-dome and horizon line, are subject to optical illusion, supporting his statement that Light bends in wide arcs through space, rather than travelling in straight paths. As such when we believe we are looking at a luminous astrological object perpendicular to our line of sight, what we are seeing actually lies on the other end of a bent ray of light. Thus ones line of sight is really pointing at nothing, and their eyes are receiving an image of something that is at a position in the sky elsewhere to the direction they are truly looking.

This arcing nature of light therefore would attribute illusion to the perception of phenomena in the sky and space. However it is not just the light alone that produces this illusion, but also the magnetic field of the earth and gravity which causes the light to behave extraordinarily.
Double refraction and re-focalisiation of light was the explanation Teed offered for the sky-dome Illusion. Teed's model however theorised a stationary sun with which he attributed the bizare notion that it were really a focalsied point of light emanating from a rotating luminous double helix at the centre of the cosmos. Abdelkader's model on the other hand requires more elaboration as it entertains an orbiting sun rather than a stationary one.

http://www.theflatearthsociety.org/forum/index.php?topic=50167.0#.VS2GjyhWzpA

 

[Hevach]

So, an offset Dyson Sphere combined with... something like Abraham's discredited model of gravity (basically the opposite of Einstein's - in Abraham's model, time was fixed but the speed of light was variable, making linear distance a relative measure).

Depending on exactly how the whole light bending thing works, the ground could appear to be flat to infinity, domed, or bowled. I'd have to figure out his math to tell which and... I just don't care that much.


What jumps out at me is that the model depends on Earth's magnetic field influencing light to create the whole optical illusion. This creates a lot of problems:

1. Magnetic fields have no effect on photons in a vacuum. They can have an effect on photons in matter, but not by changing its trajectory - only polarization.
2. This effect has never been observed in other magnetic fields (and we've tried, though not for this reason - that's how we know point 1). The earth's magnetic field is very large, but its surface strength is very weak. Its strongest points are about 0.65 gauss. By comparison, the strongest magnetic field ever created by humans was 914,000 gauss. Those useless therapy magnets run up to almost 8000 gauss, and you can get 14000 gauss magnets at many hardware stores.
3. Magnetic fields have no effect whatsoever on neutrinos. When a university wants to use their neutrino detector, they call somebody up with a neutrino source, and they point it straight through the Earth at the detector (Neutrinos barely react with matter, so even if this has to pass through the entire bulk of the planet most of them will still reach the detector - for that matter, most will pass by the detector as well).

 

[sharpnfuzzy]

There is a fairly simple experiment that you can do that shows the curvature of the earth and lets you see the sun set twice in one day. You need to be on a west facing beach of a large body of water where the other side is beyond the horizon. Ocean, sea, or great lake, will all do. Then lay flat facing the sun with your eye level as close the the ground as possible. Wait for the sun to set and as soon as the last bit disappears jump to your feet while in the same spot and you'll see the sun set again. Or reverse everything and see the sun rise twice.

If you take some simple measurements you can even calculate the earth's circumference.

Or you could take an elevator ride up the Burj Khalifa at sunset and see the same thing.

 

[Chew]

There is an ancient mariner navigation technique called "bobbing the light". An officer would go up and down ladders or rigging until a light or navigation mark was just on the horizon. If you know the height of the object and your height of eye you can calculate the distance to the object. I talked several Officers of the Deck into trying this on several of my boats while we were at periscope depth. He would order the boat to slowly go shallower or deeper. The ranges I got were accurate to within a nautical mile.

 

[Hevach]

Oh, another one issue that didn't occur to me last night, the shell-earth's gravity also plays a role in the bending of light and the movement of the cosmos inside it.

http://en.wikipedia.org/wiki/Shell_theorem

A hollow shell exerts zero net gravitational force on any object inside it, regardless of its location within the shell.

This rule holds true in Abraham's model (mentioned above), so the whole anomalous measure of distance (which lets the center of the shell be infinitely distant from all points on it, but opposite points on the shell still be 8000 miles apart) won't eliminate this effect.

This includes objects in direct contact with the sphere, by the way, meaning in a hollow earth you could get into space by dropping a toothpick - the equal and opposite reaction would be enough to reach escape velocity (it would be a very, very slow ascent, but escape velocity is literally 0, so you'll get there eventually).

 

[tadaaa]

can't you just say you have stood on top of Mount Everest, and the Earth does indeed curve

 

[Mick West]

If they think this is evidence, then why don't they do 100 miles, at 3 feet elevation?

Arguing with flat earthers (or concave earthers) is generally a waste of time. Many of them are essentially just trolling - arguing a case as a funny intellectual exercise. Then there are some who take it more seriously who use the work of the first group, but often don't really understand it.

But back to this, it seems like a variation of the eponymous "Bishop Experiment"
http://wiki.tfes.org/Experimental_Evidence

California Monterey Bay is a relatively long bay that sits next to the Pacific Ocean. The exact distance between the extremes of the Monterey Bay, Lovers Point in Pacific Grove and Lighthouse State Beach in Santa Cruz, is 33.4 statute miles. See this map.

On a very clear and chilly day it is possible to see Lighthouse Beach from Lovers Point and vice versa. With a good telescope, laying down on the stomach at the edge of the shore on the Lovers Point beach 20 inches above the sea level it is possible to see people at the waters edge on the adjacent beach 33 miles away near the lighthouse. The entire beach is visible down to the water splashing upon the shore. Upon looking into the telescope I can see children running in and out of the water, splashing and playing. I can see people sun bathing at the shore and teenagers merrily throwing Frisbees to one another. I can see runners jogging along the water's edge with their dogs. From my vantage point the entire beach is visible.

IF the earth is a globe, and is 24,900 English statute miles in circumference, the surface of all standing water must have a certain degree of convexity--every part must be an arc of a circle. From the summit of any such arc there will exist a curvature or declination of 8 inches in the first statute mile. In the second mile the fall will be 32 inches; in the third mile, 72 inches, or 6 feet, as shown in this chart. Ergo; looking at the opposite beach 30 miles away there should be a bulge of water over 600 feet tall blocking my view. There isn't.

Actual images of people playing on a beach would be much more significant evidence than some flashes of light. So why not simply take a photo of someone standing on the Antioch Pier, from the Benicia viewpoint?

And given that there are literally millions of combinations of locations in which you could do this simple experiment with a telescope, and millions of people who own telescopes, then why is the internet not flooded with millions of examples of this evidence?

If I still lived near the sea, I'd pop down an try to take photos of the beach at Point Dume (20 miles from Venice).

 

[Trailblazer]

California Monterey Bay is a relatively long bay that sits next to the Pacific Ocean. The exact distance between the extremes of the Monterey Bay, Lovers Point in Pacific Grove and Lighthouse State Beach in Santa Cruz, is 33.4 statute miles. See this map.

On a very clear and chilly day it is possible to see Lighthouse Beach from Lovers Point and vice versa. With a good telescope, laying down on the stomach at the edge of the shore on the Lovers Point beach 20 inches above the sea level it is possible to see people at the waters edge on the adjacent beach 33 miles away near the lighthouse. The entire beach is visible down to the water splashing upon the shore. Upon looking into the telescope I can see children running in and out of the water, splashing and playing. I can see people sun bathing at the shore and teenagers merrily throwing Frisbees to one another. I can see runners jogging along the water's edge with their dogs. From my vantage point the entire beach is visible.

That's a very good telescope. A person, say, 3 feet wide, at a distance of 33 miles, has an angular diameter of about 3.5 arcseconds. That's not far off the limit for ground-based telescopes at low altitude looking straight up, I would be very surprised if you could resolve something that size while looking across 30+ miles of turbulent air above the ocean! Evidence please...

 

[Mick West]

Here's an attempt to do this by a Flat Earther:
http://www.theflatearthsociety.org/forum/index.php?topic=62813.msg1661347#msg1661347

The problem with this is the math is wrong. 12.9 feet is the amount obscured when you are at 0 feet. At 2 feet it's 4.75 feet.

[Edit] The original thread for that photo is here:
http://www.theflatearthsociety.org/forum/index.php?topic=60895.0#.VS6o3RPF-Z4
There's quite the variety of attempts at math there, the correct figure of 4.75 feet is arrived at on the first page, but they still keep talking. Presumably because they don't trust the math, because they can't do it themselves.

 

[Mick West]

The above math actually gives a larger obscured portion for the OP setup though. 92.6 feet for a 45 high observer at 20 miles. (distance to horizon is 8.21 miles). Seems like they were simplifying. Not a significant difference though.

 

[Mick West]

Here's a sharable copy of that spreadsheet. Math is my own, but it's just pythagoras.
https://docs.google.com/spreadsheets/d/1xoAZqxi3FYUEv9q5Cpm-98tj3PDqWeHDN7SrOifj20g/edit?usp=sharing

 

[Pete Tar]

Can someone show me the steps for that 'solve for x' operation? Why is there one that's a negative and one that's not?

 

[Mick West]

Can someone show me the steps for that 'solve for x' operation? Why is there one that's a negative and one that's not?

(Unspoilered for the common good)

It's just a quadratic equation being solved by the quadratic formula. Any equation on the form ax^2 +bx + c has two solutions (-b +/- sqrt (b^2 - 4ac))/2a, so you just expand the equation to get the three coefficients, a,b,c and slot them into the formula.

Edit, and I used Wolfram Alpha, as I'm lazy. But here's the working.

Notes:

• "a" is the distance to the horizon, already simply worked out from r and h as sqrt((r+h)^2-r^2)
• Unfortunately I also use "a" to indicate the square coefficient
• All numbers have both a positive and negative square root, for example sqrt(4) is both 2 and -2 (2*2 = 4, -2*-2=4) so you get two results that solve the equation.
• We only use the positive result, as the negative result is on the other side of the planet.

This uses the intermediate variable "a", the distance to the horizon, if we expand the intial formula, we get:
(r+x)^2=r^2+(d-sqrt((r+h)^2-r^2))^2
https://www.wolframalpha.com/input/?i=(r+x)^2=r^2+(d-sqrt((r+h)^2-r^2))^2
which solves to a single equation in terms of d, h and r
x = sqrt(d^2-2*d*sqrt(h*(h+2*r))+h^2+2*h*r+r^2)-r

 

[Tycho's Nose]

Both the laser experiment and the Bishop experiment were performed over open water on the West Coast, where a shallow atmospheric inversion (the marine layer) is usually present. This will almost always result in a superior mirage or looming effect as discussed above. The Navy has performed studies of this type and found that meteorological conditions can affect the apparent position of lights across Chesapeake Bay (abstract here).

In effect, it's not the earth that's concave, it's the reference beam that's convex.

 

[Soulfly]

Here we go, I have seen these videos before but didn't think to suggest it here as an experiment to prove the Earth is not flat.
I believe this sort of experiment is relatively easy to get permits (if needed) for and cheap enough now a days to do. GoPro and a weather balloon.

 

[Jeremy]

Have any flat earth advocates ever posted on the Metabunk forums before?

 

[David Ridlen]

Thanks all for the responses!!

Tell those yahoos to back up another 20 miles and try it again.

Well, their laser diffuses much more at that distance. But I think their 20 mile example deserves explanation.

why is there a "horizon" at all, if the Earth's is concave?

The concave simulations I've seen dont reflect the actual dimensions concavers describe. They claim the glass sky is 100 km up, but the animations depict more like a 3500 km altitude. The Sun is a dome shape with a black backside, and is about 140 km in diameter. That means the Sun is wider than the distance between the Earth and glass sky, and only a few dozen kilometers from the ground.

So here's a brief, rough, preliminary interpretation I rendered (I think I am the first debunker to bother). It raises many questions, and I'm sure I will be corrected. I left out the 2nd glass sky inside somewhere, I am not clear on.
Unlisted link-

One thing I wonder is how solar flares would not wipe us out.

The "bendy light" thing is a convenient catch-all explanation for why Earth looks convex. It's like explaining how an apple can look and feel exactly like an orange, when a simpler explanation would be that it actually is an orange. But I have not seen a clear illustration of how bendy light supposedly works. The Sun would still have to set and rise UP behind the edge of the glass sky, instead of DOWN below the horizon. I dont see how they can explain that away.

There is a fairly simple experiment that you can do that shows the curvature of the earth and lets you see the sun set twice in one day.

Actually, the 'double sunset' should also occur if the Sun were setting below the edge of a flat Earth, which it cant do in FET. And they can never logically defend the "spotlight" sun hypothesis. But concavity dictates the Sun revolving inside Earth.

can't you just say you have stood on top of Mount Everest, and the Earth does indeed curve

I understand that Earth curvature only barely becomes noticeable at about 70,000 feet.

If they think this is evidence, then why don't they do 100 miles, at 3 feet elevation?

Haze tends to obscure at that distance, their Radioshack lasers dont go that far, and their consumer cameras dont zoom so far, and that may be difficult to arrange. But thats why I posted examples of Toronto well below sea level at 30+ miles off. But they harp on these laser and visual experiments.

It is a legitimate question, why objects are visible when they should be physically behind the 'hump.' An easy explanation is "refraction" "looming," but I was hoping to be more specific about how it is normal to expect refraction to 'subtract curvature height by Y amount, over Z distance,' that adequately and clearly explains their examples.

As I mentioned, I read that surveyers use a rough 7%-rule for refraction, but that does not seem to explain this 20 mile example.

And given that there are literally millions of combinations of locations in which you could do this simple experiment with a telescope

There are several other such daytime video examples. One that may be more clear, uses a camera about 1 ft above sea level that can clearly see a ferry at 6.6 miles away, which should not be possible due to curvature over geometric line of sight.

Again, I was hoping to find a more specific explanation than just "refraction is doing something."

Arguing with flat earthers (or concave earthers) is generally a waste of time. Many of them are essentially just trolling - arguing a case as a funny intellectual exercise. Then there are some who take it more seriously who use the work of the first group, but often don't really understand it.

Individuals vary in commitment to the idea. Some really take the whole friggin' denial bakery. But I do get thru to some, or at least get them doubting. I find that most are religious fundamentalists, struggling to force Earth back to the center of an anthropocentric universe. It is truly depressing to see thousands of subscribers to the prominent flat/concave advocate channels. Since 97% of the pro-comments are riddled in spelling and grammatical errors, I suspect most are teens.

I cannot debunk one conspiracy without having to debunk several overlapping ones. NASA must be lying for 50 years. And the 'fake' Apollo landings were just a distraction for the government killing JFK. I point out 50+ other space agencies around the globe, then they claim something about Illuminazi-jewmasons, CIA-NWO, reptilian, trilateral, whatever. If I debunk all that, in short order someone claims Satan is behind it all. And since god made Satan, I have to ultimately debunk god. This is how it goes.

I have seen these videos before but didn't think to suggest it here as an experiment to prove the Earth is not flat.

Those numerous high-altitude balloon videos are not useful evidence since they all use a wide angle lens with considerable barrel distortion, so everything looks curved. The highest I've seen is 120k feet. Thats why I link to the Soyuz Launch Camera, or the recent Space X launch. Those are the only somewhat continuous shots I found of a camera traveling from the ground to space.

 

[Mick West]

There are several other such daytime video examples. One that may be more clear, uses a camera about 1 ft above sea level that can clearly see a ferry at 6.6 miles away, which should not be possible due to curvature over geometric line of sight.

Again, I was hoping to find a more specific explanation than just "refraction is doing something."

1 foot above sea level will only obscure 19 feet of something 6.58 miles away. 28 feet is the amount obscured at 0 feet.

And they chose the Pride of Rotterdam (or one of it's sister ships), one of the largest ferries in the world.

(For scale, see the people on the upper decks)

The photo I used has some perspective, but I scaled it so the front of the shop is the right size, hence the region indicated by the arrow.

 

[Psychic]

From an online Wired article titled 'Can you see the curvature of the Earth in this airport?' http://www.wired.com/2014/03/see-curvature-earth-airport/

If the Earth is a sphere, I can draw a circle all the way around it. Now if I am standing on the Earth and shoot a laser tangent to the surface, that would be straight line. I can represent both this circle and line as equations (assuming the origin is at the center of the Earth).

If I solve for the y-value of the circle (in quadrant 1), I get:

The difference between y1 and y2 will give the vertical deviation between a straight laser and the curved Earth. But wait! This is actually cheating. This will give the deviation in the y direction, but maybe it should be a radial deviation. Of course, I am going to proceed anyway – I suspect that for small distances the difference between radial and y distances will be small. Also, there is only one horizontal variable in the two equations – x2. I'll just call this x. Here is the deviation as a function of x.

Just for simplicity, I called this deviation distance s. So, what is the deviation value for a laser aimed across a "level" airport terminal? Putting in the value of 726 meters as well as the radius of the Earth, I get a deviation of 4.1 cm.

It shouldn't be terribly difficult to try this, and refraction should not be a consideration because it's indoors.

Note also that the writer gives the terminal a length of ~700 metres - I recall reading about a hallway in a Chinese university that was two kilometres long (therefore the curvature of the Earth should be visible just by looking down the corridor) but I cannot find the article with Google.

Edit - That last bit seems to be incorrect - according to the Wikipedia article on an RAF station in the Falklands called 'Mount Pleasant', an 800-metre corridor on the base is the longest in the world.

 

[David Ridlen]

1 foot above sea level will only obscure 19 feet of something 6.58 miles away. 28 feet is the amount obscured at 0 feet.

Using people from the deck for height reference, it looks like an approximate 14 to 15 foot difference. Should we assume the remaining 4 to 5 feet of difference are due to refraction? Or maybe the camera is a bit higher than 1 foot above sea level.

Higher resolution-
https://www.metabunk.org/data/MetaMirrorCache/32f6a580b01016129868740b4d8e59a7.jpg

 

[Trailspotter]

Using people from the deck for height reference, it looks like an approximate 14 to 15 foot difference. Should we assume the remaining 4 to 5 feet of difference are due to refraction? Or maybe the camera is a bit higher than 1 foot above sea level.

A smooth spherical surface representing the average sea level is an approximation. There are unaccounted tidal effects in these calculations that may explain a few feet discrepancy.

 

[Trigger Hippie]

These calculations use the radius of the earth. Since the earth is not a perfect sphere, the radius value they use is typically the mean value. So that can also account for some of the error.

 

[David Ridlen]

1 foot above sea level will only obscure 19 feet of something 6.58 miles away. 28 feet is the amount obscured at 0 feet.

The height difference does not make sense to me. How can a 1 foot increase in camera height result in subtracting 9 feet from the peak of Earth bulge height, halfway between the camera and the hull water line?

 

[Trailspotter]

The height difference does not make sense to me. How can a 1 foot increase in camera height result in subtracting 9 feet from the peak of Earth bulge height, halfway between the camera and the hull water line?

The peak of bulge height is not halfway between the camera and the hull water line, but is much closer to the camera than to the hull. At 0 feet it is where the camera is.

 

[Mick West]

The height difference does not make sense to me. How can a 1 foot increase in camera height result in subtracting 9 feet from the peak of Earth bulge height, halfway between the camera and the hull water line?

The "bulge height" is not what is being calculated here, it's how much of the target object is being obscured. What FE fans often calculate as the "bulge height" is actually the amount obscured if viewed from sea level (0 feet)

Bulge height is something different again.

 

[David Ridlen]

The peak of bulge height is not halfway between the camera and the hull water line, but is much closer to the camera than to the hull. At 0 feet it is where the camera is.

? Shouldn't the bulge always be half the distance between observer and target? This is what I mean. I keep seeing different ideas on how to figure this. Shouldn't this bulge be what matters when trying to figure how much a distant object is obscured?

https://www.metabunk.org/data/MetaMirrorCache/1f4409e69f1a5856f567cf6727268b32.gif

 

[Trailspotter]

? Shouldn't the bulge always be half the distance between observer and target? This is what I mean. I keep seeing different ideas on how to figure this. Shouldn't this bulge be what matters when trying to figure how much a distant object is obscured?

https://www.metabunk.org/data/MetaMirrorCache/1f4409e69f1a5856f567cf6727268b32.gif

No, the bulge is at the horizon, and the distance to the horizon depends on the height of the camera/eyes above the sea level.
One can see objects behind the horizon if they high enough to stick out.

 

[Mick West]

Notice in your diagram, the camera cannot even see the top of the bulge.

The problem here is using the term "bulge" instead of "amount of the target that is obscured"

The actual bulge heigh b between two point a distance d apart is given by:

For 6.58 miles, this is 7.21 feet, not 28.

 

[Mick West]

No, the bulge is at the horizon, and the distance to the horizon depends on the height of the camera/eyes above the sea level.

Not really. When the camera height is zero, the horizon is at the camera position (distance to horizon = 0), so your "bulge" height would also be zero.

 

[Trailspotter]

Not really. When the camera height is zero, the horizon is at the camera position (distance to horizon = 0), so your "bulge" height would also be zero.

????
No, in 'my' definition, the "bulge" height depends on the distance between the observer's horizon and the object behind the horizon. In this case, just the distance between the camera and the hull.

http://en.wikipedia.org/wiki/Horizon