Claim: Moon's terminator as a evidence for distant sun

[Rossi]

Hi friends. I kinda believe in Flat Earth, to be honest, I don't have too much mathematical and geometric knowledge but i am willing to learn more about everything. I'm open to many ideas and I like to understand all propositions and see if they make sense to me, and I don't get too attached to any one in particular. So, I read about this topic on a brazilian blog by a college physics professor. The point is, we can attest to the greater distance of the sun from the earth than the moon from the earth by taking a sphere and comparing its terminator to the moon's terminator. He said:

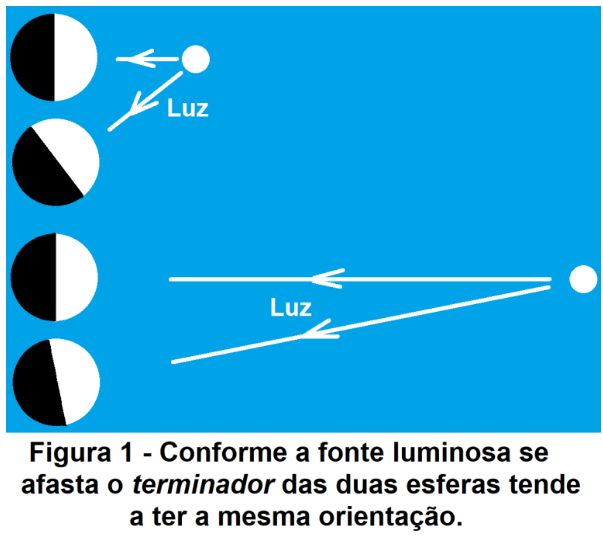
"If we imagine two spheres illuminated by a light source (see Figure 1) it is easy to conclude that the orientation of the terminator is very different when the distance between the spheres is similar to the distance from the light source to each sphere. As the distance from the source to the illuminated spheres grows, the orientation of the two terminators becomes closer and closer as shown in Figure 1."

"Figure 2 shows four photographs of the ball and the Moon (on 07/16/2017 the waning moon occurred) and in them the terminators of both can be seen with the same orientation."

"Since the terminators of the ball and the Moon are similar, the Sun illuminating both must be at a much greater distance from the Earth or the Moon than the Earth-Moon distance."
I can't see how it could work on a flat earth with sun and moon not very far to each other.

I disconsider the ideia of the moon having its own light. Its very clear through observations of the moon and its craters with the perfect contrasts of light and shadow, as well as its sphericity observing the difference with which its extremities move less than its center.

It actually makes sense, but my question is, can we create a formula using variables like the distance between the two spheres, distance between each individual sphere to the light source, diameter of the spherical light source (since the sun, due to its large diameter, has its solar rays falling on the earth with a variation of 0.53º) to determinate de angular difference between the two terminators? It would be great if someone could do it. I tried it by myself, but I don't have too much geometric and optical knowledge to do so, if someone could do it, it would be very cool. By doing it, we could take many photos like this above, in different moon phases and compare the results using both, Spherical and Flat model numbers of the sun and moon distance to see which fits better the results. Thanks

 

[Mendel]

By doing it, we could take many photos like this above, in different moon phases and compare the results using both, Spherical and Flat model numbers of the sun and moon distance to see which fits better the results. Thanks

You put your request very well,

Before I get into the maths (in another post), let me point out that the angle from the observer to the spheres matters as well for the apparent orientation of the terminator, which is why in these photographs the ball is always held close to the moon (ideally it should cover it, but that makes two photos necessary).

diameter of the spherical light source (since the sun, due to its large diameter, has its solar rays falling on the earth with a variation of 0.53º)

i feel that this effect should be neglible as a) it affects both spheres equally, and b) we intuitively put an "average" terminator in the fuzzy penumbra region.

 

[JMartJr]

Well poot, I thought I had an original idea there...

 

[DavidB66]

Well poot, I thought I had an original idea there.

As the Bible says (Ecclesiastes?), there is nothing new under the sun. Appropriately enough, in this case.

I've seen various people, including Aussie pilot Wolfie6020, giving similar demonstrations on YouTube and elsewhere. It would be hard to establish who was the first.

Flat Earth seems to be pretty much dead these days, but as I recall, flat-earthers used sometimes to argue that the moon terminator looked impossible to be explained by the reflected light of the sun, therefore the moon was self-illuminated, therefore conventional science was all wrong. Like almost everything in flat earth 'theory', the idea that the moon is self-illuminated goes back to Samuel Rowbotham in the 19th century. Rowbotham had some important reason for wanting the moon to be self-illuminated, but I forget what it was.

The value of comparing the moon with a tennis ball (or similar) is that we know the ball is not self-illuminated, but lit by the sun, yet it shows a terminator with the same orientation as that of the moon. This demonstrates practically that the terminator of the moon is consistent with illumination by a very distant sun, even if it does not strictly prove it.

 

[Rossi]

You put your request very well,

Before I get into the maths (in another post), let me point out that the angle from the observer to the spheres matters as well for the apparent orientation of the terminator, which is why in these photographs the ball is always held close to the moon (ideally it should cover it, but that makes two photos necessary).

True, I had not thought that this would completely change our perspective on sphere terminators. I made a simple model in blender to compare the different results using different camera positions. I rendered 4 images using two spheres of radius equivalent to one meter, with a distance between their centers being 4 meters and the distance from both spheres to the light source (spherical) being approximately 8.25 meters (since the light source is at a distance distance of 8 meters from the center shared by the two spheres in the horizontal plane y).

I think Blender can be a powerful tool to check the result of a possible formula to this.

 

[Rossi]

As the Bible says (Ecclesiastes?), there is nothing new under the sun. Appropriately enough, in this case.

I've seen various people, including Aussie pilot Wolfie6020, giving similar demonstrations on YouTube and elsewhere. It would be hard to establish who was the first.

Flat Earth seems to be pretty much dead these days, but as I recall, flat-earthers used sometimes to argue that the moon terminator looked impossible to be explained by the reflected light of the sun, therefore the moon was self-illuminated, therefore conventional science was all wrong. Like almost everything in flat earth 'theory', the idea that the moon is self-illuminated goes back to Samuel Rowbotham in the 19th century. Rowbotham had some important reason for wanting the moon to be self-illuminated, but I forget what it was.

The value of comparing the moon with a tennis ball (or similar) is that we know the ball is not self-illuminated, but lit by the sun, yet it shows a terminator with the same orientation as that of the moon. This demonstrates practically that the terminator of the moon is consistent with illumination by a very distant sun, even if it does not strictly prove it.

I can assure you that the flat earth community in Brazil is very much alive and growing every day. I left the Brazilian flat earth groups on social medias because they are very hostile, they do not accept being contradicted in any way, if that happens, they call you alienated by the system, I asked the same question about the terminators, none of them managed to help me to create a formula and focused on the point that the moon having its own light would make this argument nonsensical, but you can't say that the moon has its own light based on observations, so they go on to say that the light is a hologram.

 

[AmberRobot]

You don't even need two spheres. It is easily shown (using trigonometry) that the Sun is substantially farther away from the Moon by looking at the phase angle of the Moon versus the angular distance between the Sun and Moon in the sky.

For example, picture the angle between the Sun and Moon is 90 degrees. If the Sun and Moon were the same distance from us then the phase angle would be quarter moon. In fact, it is half moon, which attests to the much greater distance of the Sun.

If you go through the trig to calculate the relationship between the phase angle and the angular separation the sky as a function of the ratio of Sun to Earth and Moon to Earth distances you'll see that you need to be able to measure the phase angle to arcminute level accuracies to get the proper distance ratio, but you don't need to do it that well if you're just trying to demonstrate that the Sun is at least an order of magnitude farther away than the Moon.

I note that it is one of my pet peeves when seeing "artists conceptions" of planets illuminated by their parent stars that this is gotten wrong virtually all of the time. They want to make a drawing that shows the planet and its star in the same field of view but then over illuminate the planet, suggesting the star is very close, and thus very small.

And to the flat Earth hypothesis, be aware that there is no model of the flat Earth that correctly predicts the easily observable/measureable movements of objects in the sky. Everything I've seen presented falls flat on its face after even the most modest application of mathematics. It simply does not conform to reality.