Lake Balaton Laser experiment to determine the curvature of the Earth, if any.

[Sandor Szekely]

I've suggested several times to @Sandor Szekely, that it would be far better to use a fixed point (like a headland) in the middle and end, rather than a boat. Then accurate measurements could be taken. But he prefers the boat.

The calculations are a little complex, however you don't need them. You just need to show that the measurements do not lay on a straight line. The Wallace experiment demonstrates this with three points. Since Sandor is using a boat I've suggested that he takes as many measurements as possible so the curve will show through the noise.

The Wallace setup at 3 miles would be the same as the orange line here:

With the laser tilted down at 2 feet per mile.

Sandor has indicated he's going to do something more like the purple line (0.66 feet per mile, by leveling the laser at 1 mile. This will give a greater (and more apparent) deviation at 3 miles than the Wallace method of leveling at 3 miles, and then going back to the center.

This is VERY IMPORTANT:
Mick : "You just need to show that the measurements do not lay on a straight line."

Exactly! And in my opinion my type of slope corrected level measurement will give a more definite result than the Wallace type measurement. I am ready to do both, and I can find a target in position B to level the laser as Wallace did.
for example here:

 

[Sandor Szekely]

I do accept the distances are accurate. I'm just baffled as to why Sandor accepts it.

HAHA I have no other choice

I tried to figure out measurement possibility on the long distances but have not got any idea... so for now I do accept the GPS positions as accurate enough on the target distances. And GPS position is the best objective proof as well.
We are looking for a huge target hidden height of about 100 feet in the 14.3 miles distance (okay our distance will be around 13.4 miles now).

You will know me better and experience for your self that I try NOT to belive anything told but come to the right conclusion myself
I am very sceptic lol

 

[Mick West]

Mick, can you please draw me what you think I should measure as Wallace did?

He drew it himself:

The key here is that measurement are not taken from boats. There are just three sticks (described as "staves" at the time. They are fixed so their tops (or rather the visible points A, B and C) are equal heights above the waterline.

This was done on a canal, which has a very still surface, so very accurate measurements were used. It was also six miles from point A to point C, so a more significant drop. The sticks were also tall enough (13 feet above the waterline) to be well clear of the water surface to avoid both being obscured, and the effects of refraction.

This is probably best done with a powerful telescope at A. However you could do it with the laser at A, assuming you can hit the target at six miles. Both would also work. The staves at B and C would need sufficiently visible targets.

Suggested points:

However that's probably too far at 6.9 miles, you might want to try to get it something between 5 and 6 miles, so you can actually see point C from a reasonable height above the water.

There's also the challenge of measuring the height above the waterline in all three locations. It's possible to get a very accurate reading, just not trivial. But for a simple demonstration, assuming A-C is six miles, then within half a foot should work.

 

[DarkStar]

I am very sceptic lol

Skeptical is good - and part of skepticism is peer-review. It's awesome that you are listening to the concerns here.

I really look forward to your results.

To me the CRITICAL difference between Wallace and Rowbotham were two factors:

#1 (most important) Wallace didn't need to level anything to arcsecond precision. He just need a "pretty good" measurement for his targets being some height above the water level. At 6 miles even a foot wrong isn't going to matter for the target heights, you are going to see the curvature if it is there. This is VERY forgiving where even a slight amount of angle wrong on the level and your results are invalidated and we really have no way to validate the level angle. So that is my concern there.

At 6 miles it's a 6 foot high bump in the middle which should be pretty unmistakable, even with modest refraction.

CONSPIRACY THEORY WARNING: (just kidding a little bit) I honestly think that the Hawking team had the laser sighted at 3 miles out and THEN checked that this matched 'level' at the source. This is OK so long as the level was accurate enough. But I dunno -- maybe they had a professional do the leveling using some other method. Not sharing the method means it's NOT science (and this was a TV show, not a published paper but I agree with objections here -- they should have told us, even briefly). You MUST be exact and detailed about the method so others can replicate it. So I don't consider that segment of the show to be authoritative. But the helicopter disappearing was pretty clear evidence, and this doesn't depend on the telescope being leveled at all and it's not all that sensitive to the height of the telescope - which was shown as being fairly low. I would have worried more about refraction at that point.

#2 Wallace avoided the worst of the refraction by shooting 13 feet up instead of 8 inches above the water. When you take the observation also matters.

I don't know where you stand on this but Nowicki's timelapse of Chicago shows a pretty clear case of refraction gone wild:



I did a side-by-side of some of these frames:

You can easily see the horizon floating around like crazy and exposing the more distant Chicago skyline - you can see all kinds of refraction & mirage effects in the buildings, like the lit spires flickering, and you can see the top of the Willis Tower is stretched out compared to it's normal proportions.


Leveling is not easy which is why surveyors only take SHORT lines and close the loop to compute their error. And they make repeated measurements. We like to think "oh you set this up and point it over there and it gives you 0.13874387755 degrees and we're done - perfect!" but the reality of surveying is that it is HARD work and extremely error prone, and just being 39 arc SECONDS off will mean you are 6 feet off after 6 miles (5.98995' actually

I will absolutely swear to you that I only care about finding the truth - I have no other motive. I hope yours is the same.


But I've done my measurements here: http://flatearthinsanity.blogspot.com/2016/07/simple-proof-for-convexity-of-earth.html

And my measurements are EASY and very error tolerant. I just need a fairly plumb stick and some measuring tape. I only care about the SHAPE of the data so the exact values don't matter - it goes exponential at higher latitudes so it's trivial to tell the difference between exponential (even with a fairly shallow exponent) and linear data.

And my measurements agree with those taken by dozens of kids all around the world that participate in the Noon Day Project. And they agree with any solar altitude calculator which is BASED on a spherical Earth model, the values ONLY work on a Spherical Earth.

Good luck!

 

[Mick West]

CONSPIRACY THEORY WARNING: (just kidding a little bit) I honestly think that the Hawking team had the laser sighted at 3 miles out and THEN checked that this matched 'level' at the source. This is OK so long as the level was accurate enough. But I dunno -- maybe they had a professional do the leveling using some other method. Not sharing the method means it's NOT science (and this was a TV show, not a published paper but I agree with objections here -- they should have told us, even briefly). You MUST be exact and detailed about the method so others can replicate it. So I don't consider that segment of the show to be authoritative.

I agree. To determine the curve you need at least two readings at different distances to eliminate the slope of the laser. Now one of these reading can be eliminated if you already know the slope of the laser. They essentially claim it's got a slope of zero, but don't show how they measured this. I suspect the experiment was basically reversed in the way you suggest.

@Sandor Szekely will do better than this by taking lots of readings over 5 miles and plotting them on a graph. If the graph is straight, the lake is flat. If the graph is curved, the lake is curved.

 

[DarkStar]

I agree. To determine the curve you need at least two readings at different distances to eliminate the slope of the laser. Now one of these reading can be eliminated if you already know the slope of the laser. They essentially claim it's got a slope of zero, but don't show how they measured this. I suspect the experiment was basically reversed in the way you suggest.

@Sandor Szekely will do better than this by taking lots of readings over 5 miles and plotting them on a graph. If the graph is straight, the lake is flat. If the graph is curved, the lake is curved.

Yeah I agree - given the situation it's probably the best option - more measurements are absolutely a good thing no matter what the method. Over the proposed ~21km distance it should be obvious. I used to do some amateur cave surveying - not pretty. I don't think people appreciate just how difficult accurate measurement is Taking a lot of readings will help, but taking them from a boat -- whew, that is rough.

Another thing @Sandor Szekely should do is get altitude readings from GPS (at least) from all locations. We don't KNOW that the water is perfectly smooth (be it flat or merely level), we are assuming it, be good to verify that. Especially water level on both ends and in the middle (or at some fixed height above the water level so you don't get equipment wet).


I hope I made it clear in my most recent post, and Mick restated it, but what we are saying with Wallace is that, instead of trying to level the laser or calibrate it at some distance - just try to hit a distant target at a known height that ISN'T right above the water (put both the laser and target up 3 meters or so) and then see what the middle does. You could still use the boat to trace the path and take measurements.

Either the middle rises up as in Figure 1 and we have curvature or it's flat as per Figure 2.

That said. I do not believe that, at ~21km, you can hit a target that is only 3 meters above the water level from 3 meters up. I think you would need to be about 9 meters up to hit a 9 meter high target at 21km -- maybe 8m/8m with refraction (varies with conditions -- if you hit a thermal duct you could make it further of course). So you might want to have a plan in place for that (some positions up a little higher). Maybe have a camera with a good optical zoom taking a timelapse of the distance shore so we can at least see changes in the refraction index?

Whatever else, PLEASE keep things up off the water level or that will spoil it due to refraction concerns.

As for specific numbers, at 21.5km the sagitta ('Bulge' Height) should be approx 9.1 meters. Which means you need to be 9.1 meters up to hit a 9.1 meter high target (before accounting for refraction) and you use https://www.metabunk.org/curve/ to figure out whatever specifics you have and figure *about* +1/7 Earth curvature for nominal refraction.


As for the size of your laser 'spot' at 21km... Some context:

http://www.lpi.usra.edu/lunar/missions/apollo/apollo_11/experiments/lrr/
"the beam that it is about 7 kilometers in diameter when it reaches the Moon and 20 kilometers in diameter when it returns to Earth"

That's about 0.001° of dispersion to the moon with professional grade equipment - so over your ~21km that'd be about 38 cm wide maybe? Pretty wide but maybe acceptable if you can hit that level of collimation. I suspect it's going to go SPLAT and you'll need to test with much shorter distances but i wish you good luck.

 

[Spectrar Ghost]

As mentioned though, minimum possible beam divergence is inversely related to beam diameter. APOLLO achieves its tight beam by turning a 3.5m telescope into a laser reflector. A commercial laser with ~1mm beam diameter will have divergence about three orders of magnitude larger.

 

[Mick West]

If I might suggest a possibly more foolproof non-laser continuous Wallace type setup?

A = The camera, with a 500mm lens, focused on infinty.
B = A tripod that simply remains in the frame through the entire shot to prove the camera does not move
C = The boat with a 10 foot high board firmly fixed in a vertical position, with different colored rectangles at 1 foot intervals.

So you set up the camera as level as possible. You can do this various ways, but here's a suggestion

• Use a concrete jetty, or similar, with a level surface, a few feet above the water (exact height is not important)
• Setup the camera on a very solid tripod, as level as you can get by looking at it, and measure the height from the ground to the center of the camera sensor.
• Setup point B (for example the top of a tripod) as far away from point A as possible on the level jetty, so that it is the same height off the ground
• Tilt the camera so point B is exactly in the middle of the frame. Lock it in place.

Alternative simpler method:

• Focus on the far shore, which will get the camera approximately level, lock the camera tripod
• Put the other tripod (Point B) in view

With a level camera, and point B to prove it does not move. Move the boat to point C
Start videoing with the camera
Move the boat away 5 miles, keeping it in shot, stop every 1/4 mile and let the boat settle as much as possible.

So now you've got a video that contains all the measurements you need.

• Overlay a horizontal line on the video as a fixed reference plane
• For each of the 1/4 mile stopping points see at what height this line intersects the board at C. If the boat is bobbing that take the midpoint of the top and bottom of the bob (frame advance to measure accurately)
• Plot these on a graph
• See if the graph is a curve or a straight line.

 

[DarkStar]

It will be on the 15th / 16th of August ( in 10 days )

Are these still the planned dates? If so, coming right up!

 

[Mick West]

Something that might be useful for the initial leveling is that some camera have a level built in, like my old 7D:

On a Canon, just press the INFO. button a couple of times.

 

[Mick West]

If I might suggest a possibly more foolproof non-laser continuous Wallace type setup?

And if anyone does do something like this, one important fact is that nobody should move in the boat. In fact it would be better if there was just one person in the boat, and they sit in the exact same place for the entire trip.

 

[eenor]

I will study this thread more, sorry if this is already answered, but I'm trying to explain why Hawkings lake experiment was correct and conclusive without having factored the observer height (and understanding that refraction wasn't spoken of accounted for either). It appears that the laser was well above water level....so without a bunch of trig I can't fathom, is there a simple way to show why Jeranisms critique is wrong? It seems to me it should be a simple explanation if the commonly used curve formula is relevant.

 

[Mick West]

I will study this thread more, sorry if this is already answered, but I'm trying to explain why Hawkings lake experiment was correct and conclusive without having factored the observer height

Hawking's experiment, and @Sandor Szekely's, are measuring how far the surface drops. They are not measuring how much of an object is obscure from a viewpoint. Here's Sandor's own diagram:

The laster there is the upper line, it's parallel to the "Straight line from the ground" (the tangent at the pint below the camera. That distance between those lines is the "observer height", and it's just something that's added to the "drop". It's a very simple relationship, so it might seem like it's being ignored, but it's not.

If you use the curve calculator, you would put in zero for the viewer height, and then add that laser height to the result.

For Hawking, 3 Miles at 0 feet gives a 6 mile Hidden/drop, then add in whatever the laser height is (2 or 3 feet)

For Sandor his figures there are correct, basically the same thing as the Hawking experiment.

However, the Hawking experiment is NOT "conclusive" as it did not explain how the laser was leveled, and only took one reading. Sandor should do better if he takes multiple readings, which will simply show a curve, so no math is needed.

I moved your post from a different thread. I suggest you read all of this one.

 

[eenor]

Thank you being patient with me Mick, I will eagerly await @Sandor Szekely's findings, but i does seem clear that they didn't put the laser at water level (of course would be quickly obscured by lake chop) and therefore didn't actually observe 6 and 24 ft of drop from whatever laser position they started with, suggesting they just cobbled the production together with pre ordained results based on the curve calculator. Despite being TV and not science, it is amazing to me that Hawking would allow this, or is this part of the Jeranism critique still in dispute?

 

[Mick West]

Thank you being patient with me Mick, I will eagerly await @Sandor Szekely's findings, but i does seem clear that they didn't put the laser at water level (of course would be quickly obscured by lake chop) and therefore didn't actually observe 6 and 24 ft of drop from whatever laser position they started with, suggesting they just cobbled the production together with pre ordained results based on the curve calculator. Despite being TV and not science, it is amazing to me that Hawking would allow this, or is this part of the Jeranism critique still in dispute?

The 6 foot described was the change in the height of the laser spot. i.e. it was six feet above where it was previously measured at. Jeranism seems confused about what is being measured, as he refers to the "hidden" value from the viewpoint of the laser, which is entirely irrelevant. However the more general points about inaccurate measurements (it was a rough guess, but seemed more or less correct), and not demonstrating the leveling of the laser, are both valid. Hawking's laser experiment, without more information, should only be viewed as a demonstration of what you would expect. However the helicopter experiment is conclusive (although their descriptions and interpretation are not entirely accurate), you can discuss that here:

https://www.metabunk.org/stephen-hawkings-genius-helicopter-demonstration-of-lake-curvature.t7834

 

[Bass In Your Face]

Here is a graphic that shows what Jeranism is claiming.

I think Jer's overall problem with this part of the experiment is that because the laser is not known here to be "perfectly tangent", therefore its possible to get the same reading for a flat earth, but only IF we read from 2 locations and no more, and that second location to measure from is at the correct distance to give us the same change in height that matches the change in height that Globe curvature math gives us.

If we were to read from 3 locations or more, we would be able to see a linear or non-linear change in height, no matter the angle of the laser.

His other confusion has to do with, as Mick said, the change in height of the laser, and whether or not the "6 feet" is a change in height, or the actual measurement from the water.. but it's quite clear that they mean a 6 foot change.

 

[eenor]

https://www.metabunk.org/folsom-lake-photographs-demonstrating-the-curvature-of-the-earth.t7789/

Hang in there with me if you can Mick, I'm not trying to be dense but am not seeing any clarity yet in the explanations of why Hawkings Didn't make a mistake in the 6ft and 24ft measurements of curve drop. In the above Folsom lake post you use the curve calculator as is suggested by Jeranism in his Hawking Lake critique, factoring the height of your camera above the lake surface, and the from same 3 mile distance, if the Hawkings experiment is valid, I'm trying to understand why you didn't observe a 6 ft disappearance of the dock and pylons below the curve (like Hawkings lake boat did at that same distance) instead of the calculators 2.1 ft (which seems correct based on the clearly shown view). Again, thanks for being patient.

Sorry Bass, I have no idea what the flat earth diagram is showing or how it relates to the suggested error in the Hawkings experiment, but the first diagram validates to me that an observer height entry should have been used (in the video the laser hit the boat low on the hull about 2 ft above water level which should be (?) entered as observer height in the curve calculator (and...if you do it like Mick did at Folsom lake linked above). They then go out 3 miles and show the laser hitting 6 ft higher on the boat, which is only possible if they had put the laser on the surface of the lake for that distance, which as I mentioned they did not do...they started at around 2 feet above the lake. Whether they shot the laser parallel to the water surface or tangent to the horizon, it was definitely on a tripod above the lake surface. I can't yet fathom how 6 ft of laser drop can be observed over 3 miles given their setup.

Here is a graphic that shows what Jeranism is claiming.

I think Jer's overall problem with this part of the experiment is that because the laser is not known here to be "perfectly tangent", therefore its possible to get the same reading for a flat earth, but only IF we read from 2 locations and no more, and that second location to measure from is at the correct distance to give us the same change in height that matches the change in height that Globe curvature math gives us.

If we were to read from 3 locations or more, we would be able to see a linear or non-linear change in height, no matter the angle of the laser.

His other confusion has to do with, as Mick said, the change in height of the laser, and whether or not the "6 feet" is a change in height, or the actual measurement from the water.. but it's quite clear that they mean a 6 foot change.

 

[Mick West]

Hang in there with me if you can Mick, I'm not trying to be dense but am not seeing any clarity yet in the explanations of why Hawkings Didn't make a mistake in the 6ft and 24ft measurements of curve drop. In the above Folsom lake post you use the curve calculator as is suggested by Jeranism in his Hawking Lake critique, factoring the height of your camera above the lake surface, and the from same 3 mile distance, if the Hawkings experiment is valid, I'm trying to understand why you didn't observe a 6 ft disappearance of the dock and pylons below the curve (like Hawkings lake boat did at that same distance) instead of the calculators 2.1 ft (which seems correct based on the clearly shown view). Again, thanks for being patient.

Because they are two different experiments.

A) Measuring how much of something is obscured by the horizon
B) Measuring how far the surface of a lake drops below a level beam

I can see how these things are confused. It's quite a common thing to conflate the "drop" height with the "hidden" height. They are related, but different numbers.

Imagine two different lasers that are one foot above the lake, and the surface of the lake is curved, as we are on a ball.

Laser A points at the horizon, Laser B is level. They both hit a boat three miles away.

Now laser B is probably the simples to think about. It's level, so on a flat earth it would simply hit the boat one foot above the waterline. On a round earth, it would hit the boat at one foot plus whatever the drop is at three miles (6 feet)

Laser A is more complex. Let's say it's pointed at the horizon, but what does that mean? Well on a round earth, it means it's pointed at the crest of the "bulge", i.e. the last part of the surface of the lake you can see from one up. So it tilted down a bit, relative to laser B. When it hits the boat, it hits the lowest point on the boat that is visible from the viewpoint of the laser.

Think now of what Hawking's boat looks like from the shore on a round earth with these two lasers on it. It's a little over the horizon, and so 2.1 feet of the boat is hidden. Laser A hits at this point, 2.1' above the waterline. So from the viewpoint of laser A, you'd see half the dot of the laser on the boat, where the boat visually meets the horizon. The other half would be on the water.

But the boat is actually six feet lower than it was, the "drop" is six feet. So the level laser B would hit the boat six feet higher than before, i.e. at seven feet. And since 2.1 feet of the boat is hidden, you'd see the dot on the boat 3.9 feet above the dot from laser A

Try drawing it out for yourself. The key thing to get right is the difference between laser A (laser to the horizon) and laser B (a level laser). Remember laser A is going to have to dip a little.

 

[DarkStar]

They then go out 3 miles and show the laser hitting 6 ft higher on the boat,

The key phrase here is "higher on the boat" -- it's not "6 ft above the water". It's just 6 feet HIGHER.

which is only possible if they had put the laser on the surface of the lake for that distance, which as I mentioned they did not do...they started at around 2 feet above the lake.

Right, so the total height above the water would be about 8 feet. 6' + 2' The AMOUNT of drop due to curvature doesn't change just because you put the laser up 2 feet.

Whether they shot the laser parallel to the water surface or tangent to the horizon, it was definitely on a tripod above the lake surface. I can't yet fathom how 6 ft of laser drop can be observed over 3 miles given their setup.

I guess you could say it was "parallel to the water" where the laser was. I would describe it as "level" (which means perpendicular to plumb).

Consider this diagram:

The RED line that goes out to the top of D is tangent to the surface of the Earth (aka parallel to the water at the point of the observer / laser) so raise that line up 2 feet and D would increase by 2 feet.

Now you COULD angle down a little bit and hit lower on the boat with the laser but they didn't -- they tried to have the laser parallel to that red line.

Does that help?

[any calculator that is showing how much is obscured by the horizon is using the purple line which involves finding the horizon point C and then finding height of B -- this is a completely different calculation]

 

[Mick West]

The 14.3 miles laser experiment will be in August 15th - 16th
Please visit us if you are nearby Hungary and lake Balaton!

So is this actually happening?

 

[DarkStar]

So is this actually happening?

It's about 5:30pm Aug 16th just now in Hungary -- so maybe in some hours we will get an update. I'm sure it also takes time to edit the videos and make them available so who knows but would be nice to get a quick word. Was the curvature fairly obvious or do we have some 'splainin to do?

 

[Mick West]

It's about 5:30pm Aug 16th just now in Hungary -- so maybe in some hours we will get an update. I'm sure it also takes time to edit the videos and make them available so who knows but would be nice to get a quick word. Was the curvature fairly obvious or do we have some 'splainin to do?

The key thing is going to be the graph of the readings of height against distance. Everything else is just documentation.

 

[eenor]

[GALLERY=media, 38]Mirror Mirror by eenor posted Aug 16, 2016 at 9:32 AM[/GALLERY]So which curve experiment methods would I have to use to make this person (under 6 ft tall presumably) disappear from view over the curve in 3 miles (like the Hawkings Lake findings)? If the curve is that demonstrative (as Hawkings suggests), why would we see a perfect mirror reflection of the distant mountains and not one that is slightly distorted like a fun house mirror or fisheye lens? And/or is the the pictured salt flat an anomaly of flatness, or representative of water everywhere?

 

[Rory]

So which curve experiment methods would I have to use to make this person (under 6 ft tall presumably) disappear from view?

If there was no refraction, being 6 miles away from them should do it.

That's the Salar de Uyuni in Bolivia, by the way. Interesting article talking about how flat it is, and also places where it bulges slightly due to variations in the strength of gravity and dense rocks several kilometres beneath the surface here:

http://www.nature.com/news/2007/071130/full/news.2007.315.html

 

[Trailblazer]

If the curve is that demonstrative (as Hawkings suggests), why would we see a perfect mirror reflection of the distant mountains and not one that is slightly distorted like a fun house mirror or fisheye lens?

You seem to have a misconception of how pronounced the curve is. Enough curve to make a 6ft tall person disappear over 6 miles would not be anything like as curved as a "fun house mirror". The main part of the Salar de Uyuni is roughly 70 miles across. That is roughly one 360th of the circumference of the Earth, which means that the angle between the horizontal surface below your feet on one side of it and that on the far side would be approximately one degree. Do you think you could spot a one-degree distortion in a distant reflection, even if you could see right to the other side of it?

 

[Bass In Your Face]

[GALLERY=media, 38]Mirror Mirror by eenor posted Aug 16, 2016 at 9:32 AM[/GALLERY]So which curve experiment methods would I have to use to make this person (under 6 ft tall presumably) disappear from view over the curve in 3 miles (like the Hawkings Lake findings)? If the curve is that demonstrative (as Hawkings suggests), why would we see a perfect mirror reflection of the distant mountains and not one that is slightly distorted like a fun house mirror or fisheye lens? And/or is the the pictured salt flat an anomaly of flatness, or representative of water everywhere?

I think this should probably be its own thread, as it deviating from the original thread of the laser experiment.

 

[Inti]

You seem to have a misconception of how pronounced the curve is. Enough curve to make a 6ft tall person disappear over 6 miles would not be anything like as curved as a "fun house mirror". The main part of the Salar de Uyuni is roughly 70 miles across. That is roughly one 360th of the circumference of the Earth, which means that the angle between the horizontal surface below your feet on one side of it and that on the far side would be approximately one degree. Do you think you could spot a one-degree distortion in a distant reflection, even if you could see right to the other side of it?

I did a small calculation , because it often seems that people attracted to the flat earth idea can't visualise the sizes involved, and can't believe that we shouldn't see the curvature at a glance.

I found that a pretty close model of the distance we can see at when standing by the edge of the sea or on a flat plain (without refraction) is to imagine a the tip of a typical human hair touching a men's basketball. I think that puts the relative sizes in perspective (no pun intended).

 

[eenor]

Given Hawkings measurements, yea I would think we would see more of a mirrored ball effect on the salt flats and lake bed. But clearly we don't...we see a perfect un-distorted mirror image. Interestingly the person on the flats would also disappear in around 3 miles due to the effect of the vanishing point and the limits of naked eye human vision.

I'm trying to understand what my waking senses are showing me, and I do get that the globe is so huge that curves look flat, but would you agree it seems sorta odd that when we want to show a dead certain curve, its only 3 miles out, but when we see vast mirrored perfect flatness ahead (as in the above Bolivia pic) the observable curve is very very far away.

I am actually trying to understand the distinction raised above about there being two curve experiments, I appreciate your help and I think I'm beginning to understand but I'd genuinely like to know which setup method I should use to understand the curve calculator correctly.

So again, based on the Hawking laser experiment findings can I theoretically show a person drop 6ft in 3 miles on a salt flat?

 

[Rory]

Given Hawkings measurements, yea I would think we would see more of a mirrored ball effect on the salt flats and lake bed. But clearly we don't...we see a perfect un-distorted mirror image. Interestingly the person on the flats would also disappear in around 3 miles due to the effect of the vanishing point and the limits of naked eye human vision.

I'm trying to understand what my waking senses are showing me, and I do get that the globe is so huge that curves look flat, but would you agree it seems sorta odd that when we want to show a dead certain curve, its only 3 miles out, but when we see vast mirrored perfect flatness ahead (as in the above Bolivia pic) the observable curve is very very far away.

I am actually trying to understand the distinction raised above about there being two curve experiments, I appreciate your help and I think I'm beginning to understand but I'd genuinely like to know which setup method I should use to understand the curve calculator correctly.

So again, based on the Hawking laser experiment findings can I theoretically show a person drop 6ft in 3 miles on a salt flat?

Your earlier question was "how far away would you have to be for them to disappear?" (6 miles) while the question above is about a "drop" (3 miles).

Do you understand why these are different questions, with different answers?

Also, to show it theoretically, refer to the diagram on the curve calculator page.

Or perhaps drawing a circle on paper with the relevant figures will help. Doing that has always been a big help to me.

The curve, I guess, is a bit like the wind - we see the effects it produces, rather than the thing itself.

Unless one is really high.

And also: our senses are not the best measure of a thing, as optical illusions demonstrate. Indeed, to take the analogy further, wouldn't our senses tell us that trees were moving by themselves, if someone hadn't told us it was in fact the wind that was moving them?

 

[Mick West]

Also, to show it theoretically, refer to the diagram on the curve calculator page.

I think I need to add "drop" to the curve calculator. There's three related numbers: "Drop", "Bulge", and "Hidden", with the first two being only functions of the distance, and the last (also referred to as "Obscured") being a function of the distance and the observer height. These are often conflated.

This video is a bit slow, but explains the math behind them.

Source: https://www.youtube.com/watch?v=W1KJANfK71A

 

[DarkStar]

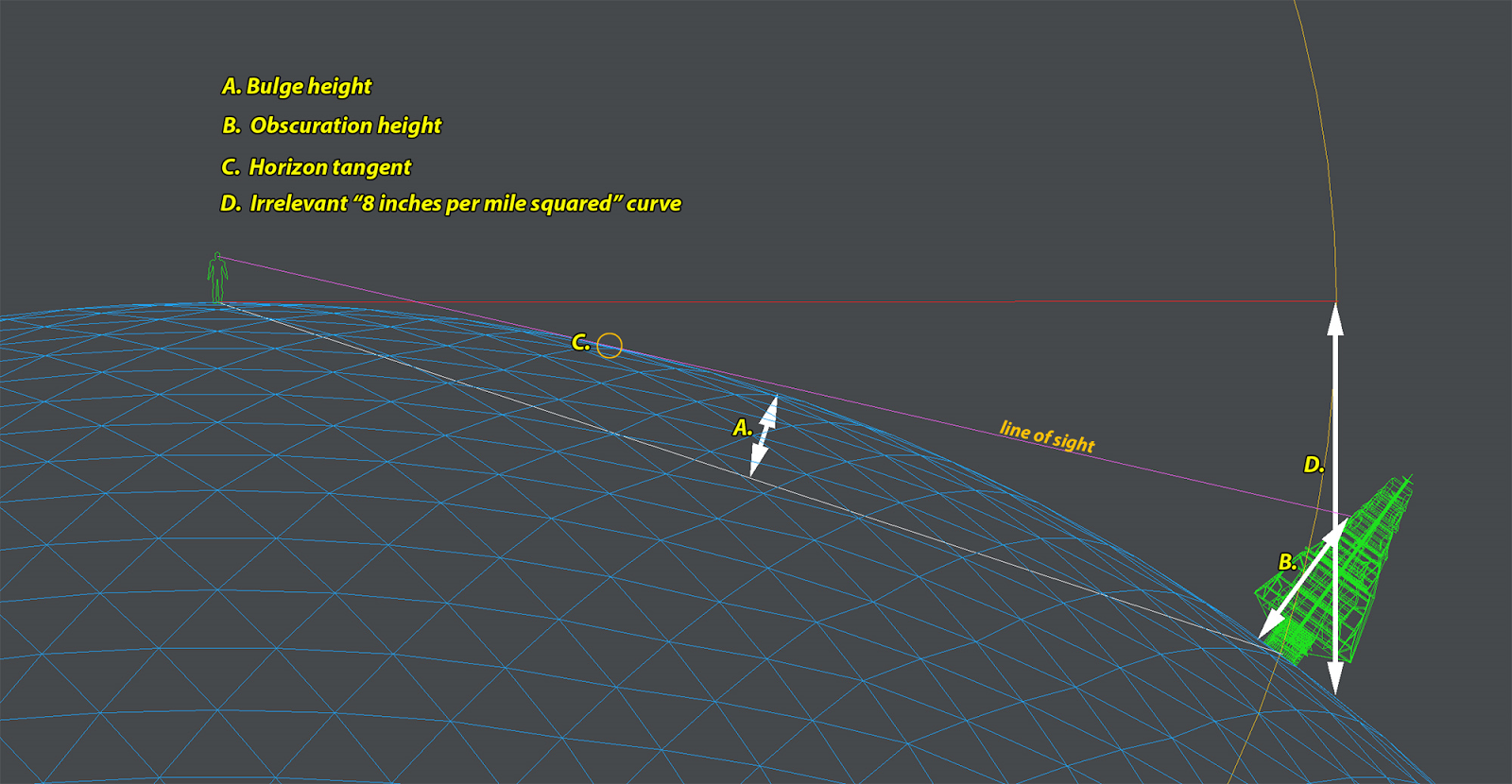
Given Hawkings measurements, yea I would think we would see more of a mirrored ball effect on the salt flats and lake bed. But clearly we don't...we see a perfect un-distorted mirror image.

Why do you think that? Have you done the math? How do you measure curvature? How do you compare it? How would you compare it to behavior on a flat plane?

What is the curvature for the Earth? How curved is that? What effect would that have on light rays?

There are mathematics to describe and work with all of these things. I can hand feed you some numbers but unless you do the work yourself to understand it you'll continue to be at the mercy of your own credulity.

Interestingly the person on the flats would also disappear in around 3 miles due to the effect of the vanishing point and the limits of naked eye human vision.

If 3 miles is the 'vanishing point' why can I see a mountain 28 miles away? Maybe you don't understand what the 'vanishing point' is? You do understand it has nothing to do with things actually disappearing right? It's the point where parallel lines would converge if you extended them to infinity.

What are the limits of human eye vision? What angular size would a 6 foot person have 1.5 miles away? Or 3 miles away? How 'big' do things appear at a distance?

I get about 0.3 arc minutes for human visual acuity (and down to 1/2 arc second under ideal conditions) -- you?

angular size(α) = 2*arctan(g/r/2) -- where r is distance to thing, and g is size of thing (in the same units) - I'll use feet here... so 2*arctan(6/15840/2) = 0.0217029465258 degrees or 1.3 arc minutes.

So that seems to be about 4.3 'human eye pixels' -- So they would be tiny but you could see them. So perhaps our intuition isn't 100% perfect and we should look more carefully eh?

Of course, don't trust just the math -- test it. You'll need a decent camera where you know the exact vertical Field Of View and you can take pictures of something of a known height at different distances and compare it with the predicted values. When you find they don't match you have to try to understand why and how to test the source of error. For example, if you test carefully you will notice that the values don't agree at different distances. That's because the FOV for your camera actually changes as it focuses closer or further away -- the values given are for focus at infinity. So you need to figure out how to adjust for that.

and then you'll find that if it's not a straight line between you you are point slightly up or down - so you need to adjust for that.

And you'll keep finding little errors like that and refining your model.

But just start with shooting pretty straight at something, keep it in the middle of the image, and see what values you get. Experiment!

I'm trying to understand what my waking senses are showing me, and I do get that the globe is so huge that curves look flat, but would you agree it seems sorta odd that when we want to show a dead certain curve, its only 3 miles out, but when we see vast mirrored perfect flatness ahead (as in the above Bolivia pic) the observable curve is very very far away.

No, I calculate that you are seeing about 1.25 miles, the rest of the land which is 'most curved' relative to you, to 3 miles out fills about 1 DEGREE of angular size because it is tilted just about completely on edge to you.

Figuring this out mathematically is pretty complex but I give you the tools here:

http://flatearthinsanity.blogspot.com/2016/08/flat-earth-follies-high-altitude.html

If the curve is barely detectable at 100,000' why do you think it should be obvious when you are at just 6 feet when you are seeing a minute fraction of the Earth?

I am actually trying to understand the distinction raised above about there being two curve experiments, I appreciate your help and I think I'm beginning to understand but I'd genuinely like to know which setup method I should use to understand the curve calculator correctly.

Ok -- there are TWO different questions:

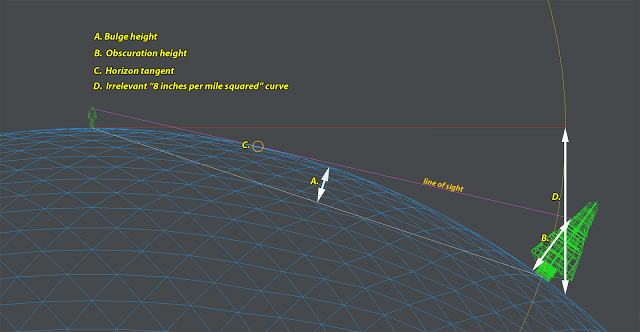
#1 how much of an object some distance away would be hidden behind the curvature if I'm at some height above the ground. Detailed math: http://flatearthinsanity.blogspot.com/2016/07/derivation-for-height-of-distant.html

Use calculator: https://www.metabunk.org/curve/

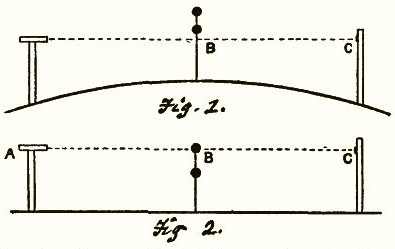
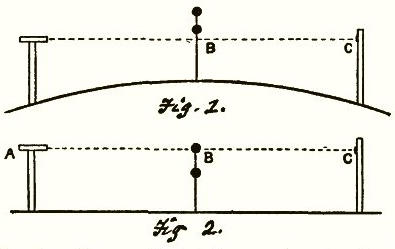
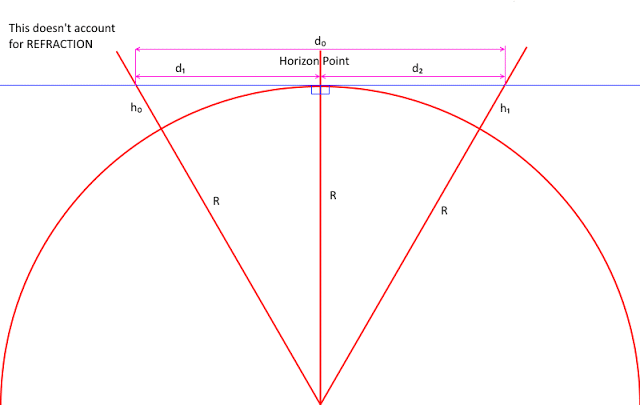
This version of the question is asking about BOTH triangles shown in this diagram.

If I'm at h0 on the left there -- I can see to some point on the Horizon and then PAST that to see some distant object so long as it's above h1 (on the right).

#2 If I had a perfectly STRAIGHT board that was X miles long and I placed it absolutely level with the ground at some point, how height above the Earth would I be after X miles?

To relate this to the diagram above This question says I am at d0 in the middle and I go d2 to the right, what is h1 at that point.


This is where people use 8" times miles squared.

Why 8" * d^2 is only an estimate that works under 100 miles:

http://flatearthinsanity.blogspot.com/2016/08/flat-earth-follies-how-to-derive-8-per.html

This is the LEVEL laser experiment case. We don't have an 'observer' height because we only want to know what the DELTA is between where the laser started and the height at some distance where we measure it. We don't care how high up the laser is in this case. It could 1000 feet up in the air -- 6 miles later the answer is STILL *24 feet higher than it was*. Make sense? I hope


Both of these are based on the SAME GEOMETRY but they are asking different questions about that geometry.

So again, based on the Hawking laser experiment findings can I theoretically show a person drop 6ft in 3 miles on a salt flat?

You are using the wrong math. If you have an observer AT ALL use the curve calculator and enter the observer height - it is IMPOSSIBLE for an observer, in practice, to have Zero height -- PERIOD.

Different parts of the image have DIFFERENT observer height! For light that passes through the TOP of the lens you need to measure from ground level to the TOP of the lens.

Let's say your height is 3 feet.

Put that into the Metabunk curve calculator as 3 miles and 3 feet you get:

Horizon distance 2.12 Miles
Hidden Amount = 0.52 Feet
'Bulge' Height = 1.5

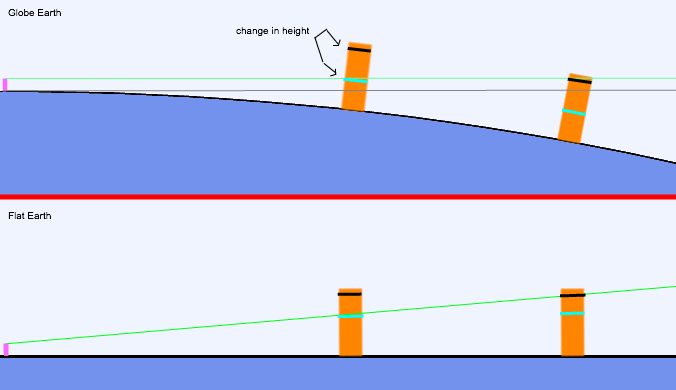
If that was a straight slope it would be just ~0.00026801029! This is VERY VERY FLAT. But's not straight, it is a VERY SLIGHT curve that is too slight for your eye to detect because of the distance. The variations on those salt flats are greater than that but you don't complain how they make it appear not flat -- that's because even those larger variations are too small for you to see.

AND, to make it harder to see, that curvature is curving down from your visual line of sight so it's ON EDGE. The last half of it fills only about 1 degree of your vision.

Write some small words on a piece of paper -- put the paper down flat on the table and put your eye down so you are viewing the paper at a very very steep angle... can you still make out the words?

Don't you think looking at 1 mile of land on edge that is a mile away, such that it takes up just 1 degree is going to be hard to see what is going on?


https://www.geogebra.org/m/ZKqBkC4A

You can move the camera and target and zoom in & play around. I'm working on one that help visualize the horizon better but it runs VERY VERY SLOWLY for some reason.

 

[DarkStar]

I think I need to add "drop" to the curve calculator. There's three related numbers: "Drop", "Bulge", and "Hidden", with the first two being only functions of the distance, and the last (also referred to as "Obscured") being a function of the distance and the observer height. These are often conflated.

This video is a bit slow, but explains the math behind them.

Source: https://www.youtube.com/watch?v=W1KJANfK71A

If you do read my analysis of 8"*d^2 formula first:

http://flatearthinsanity.blogspot.com/2016/08/flat-earth-follies-how-to-derive-8-per.html

It's not actually the D shown here -- it's the same angle as B.

 

[Rory]

Perhaps drawing a circle on paper with the relevant figures will help. Doing that has always been a big help to me.

If we take the 70-mile 'flat' surface of the Salar de Uyuni and scale it down to draw an arc of 7 inches in length, the "bulge height" of the arc will be 0.015 inches (or 0.39mm).

I imagine that would be quite difficult to observe with the naked eye, even up close.

But perhaps to get a more accurate simulation, we should place the drawing at a certain distance, like at the other side of the room.

I'd draw it if I could but me hand's not that steady.

 

[Mick West]

I've improved the curvature calculator a bit, tidying up, and added "drop" calculations
https://www.metabunk.org/curve/

Wth easier cut and paste:

For distance = 4 Miles (21120 Feet) and Viewer Height = 6 Feet (72 Inches)
Horizon = 3 Miles (15838 Feet)
Bulge = 2.67 Feet (32.01 Inches)
Drop = 10.67 Feet (128.03 Inches)
Hidden= 0.67 Feet (8.01 Inches)

I'll continue to tidy it up.

If you do read my analysis of 8"*d^2 formula first:

http://flatearthinsanity.blogspot.com/2016/08/flat-earth-follies-how-to-derive-8-per.html

I include three ways of calculating drop height,

1. r - sqrt(r^2 - d^2)
2. 8 * d^2
3. r/cos(d/r) - r

They are pretty much the same for the first 100 miles. Certainly sufficient for visual observation.

'Drop' r-Math.sqrt(r*r-d*d); drop = 1.26 Miles (6669.41 Feet)
Drop is the amount the curve of the earth drops away from level, it can be calculated in various ways
which are all about the same for under 100 miles distance
Drop calculated as 8 inches per mile squared = 8 * d*d / 12; = 1.26 Miles (6666.67 Feet)
Drop calculated with trig = r/cos(d/r) - r; = 1.26 Miles (6670.12 Feet)

 

[DarkStar]

I've improved the curvature calculator a bit, tidying up, and added "drop" calculations

Very nice, yours is my favorite already. Found one typographical oddity: "Drop' r-Math.sqrt" I suspect you meant to remove the 'Math.' package string from the text.


I have two enhancement requests, in priority order:

#1 Allow the user to enter Earth radius, but default to 3959 miles.

#2 (might be harder) allow user to pass in distance, height, and Earth radius as URL parameters so we can link users to pre-filled values.

 

[DarkStar]

@Sandor Szekely -- what's up? How did it go?

I'm starting to get worried you sunk your boat or got arrested for shining a bright laser at people.

 

[Mick West]

Sandor's email is bouncing intermittently, so he might not be getting email notification from this thread. He has not logged in since Sunday.

 

[Steve Torrence]

Just got word that the test was complete. Sander will be posting the results here soon.

 

[Mick West]

Very nice, yours is my favorite already. Found one typographical oddity: "Drop' r-Math.sqrt" I suspect you meant to remove the 'Math.' package string from the text.


I have two enhancement requests, in priority order:

#1 Allow the user to enter Earth radius, but default to 3959 miles.

#2 (might be harder) allow user to pass in distance, height, and Earth radius as URL parameters so we can link users to pre-filled values.

Done!

Click on "Permalink" to get the link with the parameters
https://www.metabunk.org/curve/?d=4&h=6&r=3959
Also added a "reset" button

 

[Mick West]

I've also added calculations based on the "Standard" refraction adjustment of 7/6 Radius. I'm not entirely sure how correct this is for all three numbers.
https://www.metabunk.org/curve/

Distance = 4 Miles (21120 Feet), View Height = 6 Feet (72 Inches) Radius = 3959 Miles (20903520 Feet)
Horizon = 3 Miles (15838 Feet)
Bulge = 2.67 Feet (32.01 Inches)
Drop = 10.67 Feet (128.03 Inches)
Hidden= 0.67 Feet (8.01 Inches)


With Standard Refracton 7/6*r, radius = 4618.83 Miles (24387440 Feet)
Refracted Horizon = 3.24 Miles (17107 Feet)
Refracted Drop= 9.15 Feet (109.74 Inches)
Refracted Hidden= 0.33 Feet (3.96 Inches)

Quite interesting the halving of the hidden amount in the above example.

At 40 miles, there's still 140 feet difference.
https://www.metabunk.org/curve/?d=40&h=6&r=3959

Distance = 40 Miles (211200 Feet), View Height = 6 Feet (72 Inches) Radius = 3959 Miles (20903520 Feet)
Horizon = 3 Miles (15838 Feet)
Bulge = 266.74 Feet (3200.83 Inches)
Drop = 1066.96 Feet (12803.56 Inches)
Hidden= 912.9 Feet (10954.75 Inches)


With Standard Refracton 7/6*r, radius = 4618.83 Miles (24387440 Feet)
Refracted Horizon = 3.24 Miles (17107 Feet)
Refracted Drop= 914.53 Feet (10974.41 Inches)
Refracted Hidden= 772.35 Feet (9268.25 Inches)