This is Folsom Lake, California. I visited it today (Aug 1 2016) to try to determine the curvature of the Earth.
Most people know the Earth is round, but they know it mostly because they just accept it, as it's long established science. But you can actually go out and test this for yourself, which can be either a fun science experiment, or a life altering paradigm shift, depending on your view of the "Flat Earth" theory.
So that viewpoint is at Brown's Ravine, a boat ramp area run by the California State Parks. Over in the distance is the dam, which is exactly 3 miles away on the right side (2.9 on the left).
I used a Canon 7D with a 500mm zoom lens, and from about 20 feet above the waterline the dam looks like this:
(Full Sized Original: IMG_0150)
Zoom in a bit more, you can see what looks like a pontoon walkway at the base of the dam.
Now as we are 20 feet above the waterline, and only 3 miles from the dam, then nothing is obscured by the curvature of the earth, as the horizon is 5.5 miles away. So we are seeing everything that is there.
So next I went down to the water, and took photos from about one foot above the surface of the water. I did not have to worry about waves, as there was just some 1" ripples. Here's the same shot from there:
(Full Sized Original: IMG_0168)
Here's a close up
Notice the walkway has gone. The water line is now above the floating pontoons, and the walkway itself. It seems like most of the hanging chains are still there though, so it's just over the walkway itself. . It's hard to see how high the walkway is, but based on the height of the safety rails, I'd say around 1 foot is it is obscured by the curvature of the Earth.
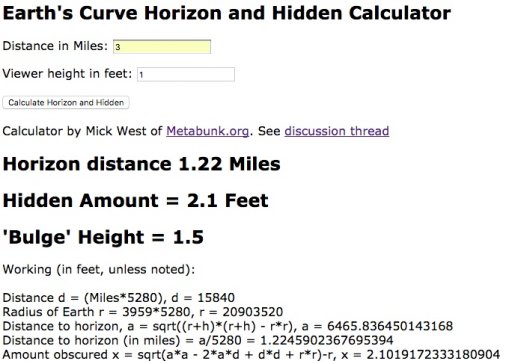
So, 3 mile distance, camera at about one foot, about one foot obscured. Is this in the ballpark? Well, if we plug in 3 miles and 1 foot camera to the calculator, we get 2.1 feet hidden, or 1.6 with "standard" refraction.
https://www.metabunk.org/curve/?d=3&h=1&r=3959&u=i
Given the very rough estimates I have for the level of my camera and the height of the pontoon walkway, this is very much in the ballpark. If my "about 1 foot" for both estimates were actually about 1.5 feet, then it would be exactly correct.
Distance = 3 Miles (15840 Feet), View Height = 1 Feet (12 Inches) Radius = 3959 Miles (20903520 Feet)
Horizon = 1.22 Miles (6465.84 Feet)
Bulge = 1.5 Feet (18 Inches)
Drop = 6 Feet (72.02 Inches)
Hidden= 2.1 Feet (25.22 Inches)
With Standard Refraction 7/6*r, radius = 4618.83 Miles (24387440 Feet)
Refracted Horizon = 1.32 Miles (6983.9 Feet)
Refracted Drop= 5.14 Feet (61.73 Inches)
Refracted Hidden= 1.61 Feet (19.3 Inches)
Hence the world is not flat.
Attachments
Last edited: