Flat Earth theory simple debunking by the moon's appearance

[mineben256]

So, after looking into some flat earth claims that where the Arctic Circle lies proves the FE, I came across an excellent piece of information that is easy to understand yet undoubtedly deals a blow to the Flat Earth theory.

It's quite simple: the moon appears upside down in the Southern Hemisphere compared to the Northern hemisphere.

This cannot be explained on a flat Earth.

 

[Chew]

It can be explained on a flat earth but only if the Moon was much farther (80 times farther) than the flat earthers claim it is. But then that would lead to a whole new slew of inconsistencies and so far none of them have been able to address the existing slew of inconsistencies of their most accepted model of the flat earth (specifically the Moon circles over a flat earth at an altitude of 3000 miles).

 

[Whitebeard]

Of course hardcore flat earthers and other deep rabbit hole dwellers don't think the moon exists at all,

In 1995, the American Historical Association, in an attempt to stifle revisionist scholarship, marked the 50th anniversary of the defeat of Nazism with a resolution calling on scholars to "initiate plans now to study the significance of the Holocaust." This, however, was not enough of a blow to free academic discourse for the enemies of truth. The president of the AHA, William Leuchtenburg, was asked why the resolution did not go so far as to explicitly recognize the Holocaust as a fact of history. He answered that for a group of historians to say that there had been a Holocaust was tantamount to "an organization of astronomers saying there is a moon."

While, on the surface, this appears as nothing more than a shameless attempt to trivialize and thereby discredit the work of revisionists, it nonetheless got me to thinking: why did this historian single out the moon? Why would a scholar, so familiar with academic standards of evidence, use such language to imply that the existence of the moon, unlike any other issue, was a given and not subject to proof? What, in other words, was he trying to hide?

It was then that I embarked on my research, which has led me to this day when I can confidently make the following assertion: The Moon does not exist. As I realize this revelation may appear shocking to the average reader, allow me to repeat it:

The Moon does not exist!

This is no lie. Until recently, I, too, believed in the traditional, establishment view of the moon. But any thinking person, untainted by the biases imposed on us by the controlled media, will have no choice but to reach the conclusion I did once faced with the facts described in this account.

Content from External Source

from - http://www.revisionism.nl/Moon/The-Mad-Revisionist.htm

But there again some folks think David Icke IS the son of god.

 

[Hofnarr]

..the moon does not exist...

No photographs were ever taken of the moon until the 1850�s. Photographs such as this one, taken in 1852 by John Adams Whipple at the Harvard College Observatory, have been cited by Lunarists as proof of the existence of the moon.

Content from External Source

So, supposedly, the "moonhologram" exists since 1850..
But what about the inca
moon goddess mama-quilla? where does she/it come from?

Next Quote from: https://en.wikipedia.org/wiki/Mama_Killa

Mama Killa (Quechua mama mother, killa moon, "Mother Moon",[1] hispanicized spelling Mama Quilla), in Inca mythology and religion, was the third power and goddess of the moon.

Content from External Source

edit: getting the ext.quotes right....

 

[Gridlock]

Here's a possible Bronze Age moondial;

http://www.livescience.com/48298-bronze-age-sundial-moondial-discovered.html

The slab is marked with round divots arranged in a circle, and an astronomical analysis suggests that these markings coincide with heavenly events, including sunrises and moonrises.

Content from External Source

I'm sure there's many more between then and 1850.

 

[Whitebeard]

..the moon does not exist...

No photographs were ever taken of the moon until the 1850�s. Photographs such as this one, taken in 1852 by John Adams Whipple at the Harvard College Observatory, have been cited by Lunarists as proof of the existence of the moon.

Content from External Source

.... err may be because photography didn't exist until around 1820, and as has been discussed elsewhere lunar photography can be tricky even these day due to issues such as contrast, exposure and focus. Add in the fact that until the 1890's and the development of fast film and rapid shutter release exposures could take over an hour and I'm suprised that there are lunar photographs as early as 1852.

But lets say for a moment that the moon IS a hoax from the 1850's....

Then what the heck is shown in these paintings?


Joseph Vernet, Night: Seaport by Moonlight, 1771, (Louvre gallery)



James Arthur O'Connor
Moonlight Scene (C. 1820) - Crawford Gallery, Cork

http://www.nationalgallery.org.uk/s...0022-WZ-PYR.tif&CNT=1&HEI=371&QLT=85&CVT=jpeg
The Four Times of Day: Evening
1739-41, Nicolas Lancret (National Gallery - London)

etc etc etc...

 

[Whitebeard]

Here's a possible Bronze Age moondial;

http://www.livescience.com/48298-bronze-age-sundial-moondial-discovered.html

The slab is marked with round divots arranged in a circle, and an astronomical analysis suggests that these markings coincide with heavenly events, including sunrises and moonrises.

Content from External Source

I'm sure there's many more between then and 1850.

Like The Antikythera Mechanism...

The delicate workings at the heart of a 2,000-year-old analogue computer have been revealed by scientists.

The Antikythera Mechanism, discovered more than 100 years ago in a Roman shipwreck, was used by ancient Greeks to display astronomical cycles.

Using advanced imaging techniques, an Anglo-Greek team probed the remaining fragments of the complex geared device.

The results, published in the journal Nature, show it could have been used to predict solar and lunar eclipses.

Content from External Source

On the back, two further dials displayed information about the timing of lunar cycles and eclipse patterns. Previously, the idea that the mechanism could predict eclipses had only been a hypothesis.

Other aspects are less certain, such as the exact number of cogs that would have been in the complete device. The new research suggests 37 gears could have been used.

However, what is left gives an insight into the complexity of the information the mechanism could display.

For example, the Moon sometimes moves slightly faster in the sky than at others because of the satellite's elliptic orbit.

Content from External Source

(from - http://news.bbc.co.uk/1/hi/sci/tech/6191462.stm )



...which shows that the ancient Greeks not only saw the moon, but understood something about its phases, orbit and it relation to other heavenly bodies.

 

[solrey]

Then there is the purely lunar Hijri calendar that is still used in the Islamic world.

The Islamic calendar (or Hijri calendar) is a purely lunar calendar. It contains 12 months that are based on the motion of the moon, and because 12 synodic months is only 12 x 29.53=354.36 days, the Islamic calendar is consistently shorter than a tropical year, and therefore it shifts with respect to the Christian calendar.

Content from External Source

https://en.wikipedia.org/wiki/Islamic_calendar

http://www.webexhibits.org/calendars/calendar-islamic.html

 

[Whitebeard]

and the fact that the 5000 year old Recumbent Stones type monuments found in Northern Scotland and the West of Ireland are all aligned with the moon rise and moon set on the winter solstice.

Recumbent stone circles are believed to have been designed for ritualistic astronomical purposes. The moon would have appeared above the recumbent stone, framed between the flankers. Scotland's recumbent stone circles have an average diameter of about 20 m (66 ft), so a recumbent stone that was 3.7 m (12 ft) long would have given an observer an arc of vision of around 10 degrees. This would have given the worshippers about an hour during which the moon would pass over the stone.


About every eighteen and a half years, the moon would make a closer approach in which it would appear to be "framed" between the two flanking stones above the recumbent; this was presumably a peak time for ceremonies. The nature of the ceremonies is unknown, but Audrey Burl suggests that "the rites enacted in the rings were closely connected with the flourishing and dying of plants, crops, animals and human beings in the short-lived world of four thousand years ago."

Content from External Source

Again showing that observation and understanding of the moons orbit and cycles was understood long before modern science got involved.

 

[Benji]

So, after looking into some flat earth claims that where the Arctic Circle lies proves the FE, I came across an excellent piece of information that is easy to understand yet undoubtedly deals a blow to the Flat Earth theory.

It's quite simple: the moon appears upside down in the Southern Hemisphere compared to the Northern hemisphere.

This cannot be explained on a flat Earth.

It's just as explainable on the flat earth model as it is on the globe. On FE, the moon travels in a circle around the earth. If you are "inside" that circle when you look up (e.g. north of the equator), it looks a certain way. If you are on the "outside" of that circle (or south of the equator) then when you look up you will see the upside down version of what's seen on the inside of the circle. You can demonstrate this yourself by holding a quarter above your head and moving from one side to the other.

 

[Mick West]

It's just as explainable on the flat earth model as it is on the globe. On FE, the moon travels in a circle around the earth. If you are "inside" that circle when you look up (e.g. north of the equator), it looks a certain way. If you are on the "outside" of that circle (or south of the equator) then when you look up you will see the upside down version of what's seen on the inside of the circle. You can demonstrate this yourself by holding a quarter above your head and moving from one side to the other.

Can you draw a FE diagram that shows the position of two people and the moon such that they see it as rotated 180 degrees?

 

[Z.W. Wolf]

The typical reply is: "Paste a flat picture of the moon on the ceiling of your living room. Look at it from one side of the room, now move to the other side and look at it again. It's upside down!"

This is why they insist that the moon is also flat. But of course, in that case it would appear oval shaped from most spots on the FE. There's also the question of exactly where this flat moon is in relation to the FE and its relation to the "firmament" - the dome.

Some flat earthers have traded pictures of the moon in the northern and southern hemisphere and have dismissed the whole notion that it is "upside down" in the southern hemisphere. The complicating factor is field rotation, which they have never heard of and don't understand when it is explained to them. For instance, they might compare a rising full moon in the northern hemisphere to a setting full moon in the southern hemisphere; and everything in between.

 

[Benji]

The typical reply is: "Paste a flat picture of the moon on the ceiling of your living room. Look at it from one side of the room, now move to the other side and look at it again. It's upside down!"

This is why they insist that the moon is also flat. But of course, in that case it would appear oval shaped from most spots on the FE. There's also the question of exactly where this flat moon is in relation to the FE and its relation to the "firmament" - the dome.

Some flat earthers have traded pictures of the moon in the northern and southern hemisphere and have dismissed the whole notion that it is "upside down" in the southern hemisphere. The complicating factor is field rotation, which they have never heard of and don't understand when it is explained to them. For instance, they might compare a rising full moon in the northern hemisphere to a setting full moon in the southern hemisphere; and everything in between.

Can you draw a FE diagram that shows the position of two people and the moon such that they see it as rotated 180 degrees?

Sure:

 

[Marin B]

Of course hardcore flat earthers and other deep rabbit hole dwellers don't think the moon exists at all,

In 1995, the American Historical Association, in an attempt to stifle revisionist scholarship, marked the 50th anniversary of the defeat of Nazism with a resolution calling on scholars to "initiate plans now to study the significance of the Holocaust." This, however, was not enough of a blow to free academic discourse for the enemies of truth. The president of the AHA, William Leuchtenburg, was asked why the resolution did not go so far as to explicitly recognize the Holocaust as a fact of history. He answered that for a group of historians to say that there had been a Holocaust was tantamount to "an organization of astronomers saying there is a moon."

While, on the surface, this appears as nothing more than a shameless attempt to trivialize and thereby discredit the work of revisionists, it nonetheless got me to thinking: why did this historian single out the moon? Why would a scholar, so familiar with academic standards of evidence, use such language to imply that the existence of the moon, unlike any other issue, was a given and not subject to proof? What, in other words, was he trying to hide?

It was then that I embarked on my research, which has led me to this day when I can confidently make the following assertion: The Moon does not exist. As I realize this revelation may appear shocking to the average reader, allow me to repeat it:

The Moon does not exist!

This is no lie. Until recently, I, too, believed in the traditional, establishment view of the moon. But any thinking person, untainted by the biases imposed on us by the controlled media, will have no choice but to reach the conclusion I did once faced with the facts described in this account.

Content from External Source

from - http://www.revisionism.nl/Moon/The-Mad-Revisionist.htm

But there again some folks think David Icke IS the son of god.

That revisionism site is satire. Or at least I sure hope it is!

 

[Mick West]

Sure:

So (besides the moon not looking flat) people to the "east" and "west" of the moon on a FE would also see 180 degree flipped version of the moon (which is not obvious from your diagram as you use a symmetrical face).

Unfortunately it's so ludicrous that I feel it's not worth debunking. Who seriously gives this explanation?

 

[Benji]

So (besides the moon not looking flat) people to the "east" and "west" of the moon on a FE would also see 180 degree flipped version of the moon (which is not obvious from your diagram as you use a symmetrical face).

Unfortunately it's so ludicrous that I feel it's not worth debunking. Who seriously gives this explanation?

The simple fact is that someone posted "proof" that the moon can't appear upside down in the southern hemisphere on the flat earth model when I showed quite simply that it can. You asked for a diagram and I gave exactly what you asked for. It doesn't have to even look flat or symmetrical for my diagram to work. My point is that the original post here is not proof that the earth isn't flat. I'm altogether aware that it's not proof that it is flat, either.

 

[huwp]

Sure:

So how does this concept account for the moon setting? If this diagram were true, the moon would never set, but instead would move away horizontally across the sky getting smaller (and more oval) as it does.

Or in this milieu, is it sufficient to explain one thing at a time and never mind if the explanations contradict each other?

 

[Mick West]

My point is that the original post here is not proof that the earth isn't flat.

It kind of is, as it contains the implied (nearly obvious) condition that the moon is a sphere - which it has to be as it looks round from everywhere in the world.

 

[Benji]

The moon being a sphere (or any other celestial object being spherical) does not necessitate the earth being a sphere. It might be a logical conclusion, but it is by no means empirical evidence.

 

[Mick West]

The moon being a sphere (or any other celestial object being spherical) does not necessitate the earth being a sphere. It might be a logical conclusion, but it is by no means empirical evidence.

The point was that if the moon was a sphere (which we can prove by it always appearing circular), you would see different parts of it from different parts of the flat earth. But you don't. That's pretty empirical.

 

[Z.W. Wolf]

The moon being a sphere (or any other celestial object being spherical) does not necessitate the earth being a sphere. It might be a logical conclusion, but it is by no means empirical evidence.

A theory has to account for all facts not just the confirming facts.

This video shows why a spherical moon circling above a flat earth cannot work. We would see the moon cycle through all its phases in one day. Also, different parts of the moon would be visible at the same time from different parts of the earth. (If the video starts at beginning go to 1:54.)

 

[Z.W. Wolf]

Sure:

A theory has to fit all the facts, not just the confirming ones.

This is why a flat moon circling above a flat earth cannot work.

- At any one moment no more than 50% of the moon's surface is visible. But long before the space age, more than 50% of the moon's surface was mapped. This article explains how that was possible. Libration - a wobble from side to side, and a "nod" up and down, shows us hidden features "around the corners" on the spherical moon.

http://earthsky.org/space/how-much-of-the-moon-can-we-see-from-earth-lunar-libration

A flat disk could not have more features "around the corners."

- A flat moon would look like an oval from most spots on earth at any one time. The farther away it was the more oval it would be. Anyone should have an intuitive feeling for that from life experience.


A flat disk moon would only work if a particular observer were in a privileged spot on the earth in which the flat disk moon would turn its face toward that spot and that spot alone as it traveled across the sky. I think this is what flat earthers are imagining when they look up at the moon - that the moon is showing them its full face at all times - without realizing that they would have to be in a privileged spot for it to work.


Neither a flat nor spherical moon circling above the earth would ever set. The perspective argument flat earthers make is only convincing on the most superficial level. If you actually make a model of the flat earth you will see that a straight line can be drawn between any spot on the earth's surface and the moon at any time.

The moon is supposedly 3,000 miles above the surface and the flat earth is 16,000 miles (or so) in diameter. That is a ratio of only 5.34 to 1. If you made a table top model of this system, if the earth were 36 inches in diameter, the moon would be 6 3/4 inches above the surface. You could stretch a string between any point on the surface of your model earth and the moon in any part of its path. Light travels in a straight line. So how could the moon ever be out of your line of sight?

If it disappeared due to atmospheric extinction, it would just fade out while still high above the horizon.

 

[DarkStar]

Another factor.

If the moon or sun were just 3000 or 4000 miles away the parallax from different locations would be fairly enormous.

For an object 4000 miles away you'd get about 8.8° parallax for every 1000km. It would be unmistakable.

GeoGebra calculator: https://www.geogebra.org/m/WDcnZwqY

This would be completely unequivocal and trivial to observe by people living at even slightly different latitudes. No solar/lunar position calculator would be even close to accurate.


With sun 149.6 million km away you get just 0.0001981409° of parallax (or 0.713307 arcseconds) for that same 1000km.

GeoGebra calculator: https://www.geogebra.org/m/XgmCSV9B

Guess which one is more accurate?

 

[Rory]

It's sure come to something when we're quoting ancient sources to show that people before 1850 also "had the moon".

I'm surprised no one's mentioned the Bible: over 40 mentions in there, apparently.

Benji, I'm not actually a hundred percent against your diagram here, and I think much of the opposition to it seems to have missed the point, that all it's intended to do is counter the OP, rather than prove anything else, and shouldn't be countered with other arguments, although related.

Still, looking at your drawing, I'm curious as to why people who are looking at an elliptical moon are seeing it as a circle?

I'm assuming you meant to draw it as a flat circle. Is that right?

If so, then your people should be seeing an ellipse.

Also, if it's flat, like a coin, they should be seeing an edge.

Or maybe you did mean to draw an ellipse? In which case they would be seeing an even more stretched ellipse.

Or perhaps you meant to draw a sphere? In which case they would be seeing something altogether different.

Can I suggest a new diagram please? And maybe one that shows how the moon would look from 4 directions, rather than 2?

 

[Inti]

The point was that if the moon was a sphere (which we can prove by it always appearing circular), you would see different parts of it from different parts of the flat earth. But you don't. That's pretty empirical.

More evidence that the moon is a a sphere is the shape of the craters. Around the rim, they appear elliptical, and become more circular the closer they are to the disks centre. And we can see that ourselves with any low cost telescope, so we don't have to rely on those conspirators at Nasa.


And if course, there the obvious shape and gradation if the shadow around the sphere when it is side-lit. Fairly compelling to anyone willing to look, which excludes most FE true believers

Dubay quotes Rowbotham, his Victorian guru, as attributing all these observed details. to pareidolia:

“Astronomers have indulged in imagination to such a degree that the moon is now considered to be a solid, opaque spherical world, having mountains, valleys, lakes, or seas, volcanic craters, and other conditions analogous to the surface of the earth. So far has this fancy been carried that the whole visible disc has been mapped out, and special names given to its various peculiarities, as though they had been carefully observed, and actually measured by a party of terrestrial ordinance surveyors. All this has been done in direct opposition to the fact that whoever, for the first time, and without previous bias of mind, looks at the moon's surface through a powerful telescope, is puzzled to say what it is really like, or how to compare it with anything known to him. The comparison which may be made will depend upon the state of mind of the observer. It is well known that persons looking at the rough bark of a tree, or at the irregular lines or veins in certain kinds of marble and stone, or gazing at the red embers in a dull fire will, according to the degree of activity of the imagination, be able to see many different forms, even the outlines of animals and of human faces. It is in this way that persons may fancy that the moon's surface is broken up into hills and valleys, and other conditions such as are found on earth. But that anything really similar to the surface of our own world is anywhere visible upon the moon is altogether fallacious.” -Dr. Samuel Rowbotham, “Zetetic Astronomy, Earth Not a Globe!”

Content from External Source

Dubay misses a weak trick by not mention Lowell and his martian canals here.

Comically, he also claims that

74) NASA graphics artists have placed things like faces, dragons, and even the word “SEX” into cloud patterns over their various ball-Earth pictures. Their recent 2015 Pluto pictures even clearly have a picture of Disney’s “Pluto” the dog layered into the background. Such blatant fraud goes unnoticed by the hypnotized masses, but provides further proof of the illegitimacy of NASA and their spinning ball planet mythos.

Content from External Source

 

[Inti]

It's sure come to something when we're quoting ancient sources to show that people before 1850 also "had the moon".

I'm surprised no one's mentioned the Bible: over 40 mentions in there, apparently.


Benji, I'm not actually a hundred percent against your diagram here, and I think much of the opposition to it seems to have missed the point, that all it's intended to do is counter the OP, rather than prove anything else, and shouldn't be countered with other arguments, although related.

Still, looking at your drawing, I'm curious as to why people who are looking at an elliptical moon are seeing it as a circle?

I'm assuming you meant to draw it as a flat circle. Is that right?

If so, then your people should be seeing an ellipse.

Also, if it's flat, like a coin, they should be seeing an edge.

Or maybe you did mean to draw an ellipse? In which case they would be seeing an even more stretched ellipse.

Or perhaps you meant to draw a sphere? In which case they would be seeing something altogether different.

Can I suggest a new diagram please? And maybe one that shows how the moon would look from 4 directions, rather than 2?

I'm not sure if this helps:


http://roundearthsense.blogspot.co.uk/2016/03/146-ball-earth-model-claims-moon.html

it was part of my reply to this claim by Eric Dubay:

145) “Heliocentrists believe the Moon is a ball, even though its appearance is clearly that of a flat luminous disc. We only ever see the same one face (albeit at various inclinations) of the Moon, yet it is claimed that there is another “dark side of the Moon” which remains hidden. NASA states the Moon spins opposite the spin of the Earth in such a perfectly synchronized way that the motions cancel each other out so we will conveniently never be able to observe the supposed dark-side of the Moon outside of their terrible fake CGI images. The fact of the matter is, however, if the Moon were a sphere, observers in Antarctica would see a different face from those at the equator, yet they do not – just the same flat face rotated at various degrees.”

Content from External Source

http://www.atlanteanconspiracy.com/2015/08/200-proofs-earth-is-not-spinning-ball.html

I didn't take account of which way up the moon looks from different hemiispheres when i drew it, though.

 

[0x90]

Sure:

This commonly-cited explanation is flawed and incomplete, primarily because it depends on arbitrary orientation of the views involved. To demonstrate, let us imagine three observers standing on the earth, at around the equinox, and at the same longitude, but different latitudes:

1. One at 45°N.
2. One at the equator.
   
3. One at 45°S.

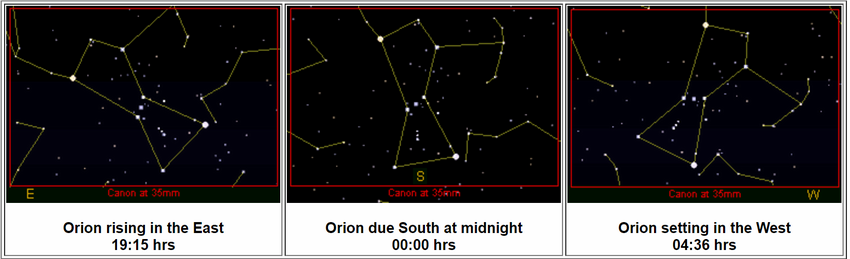
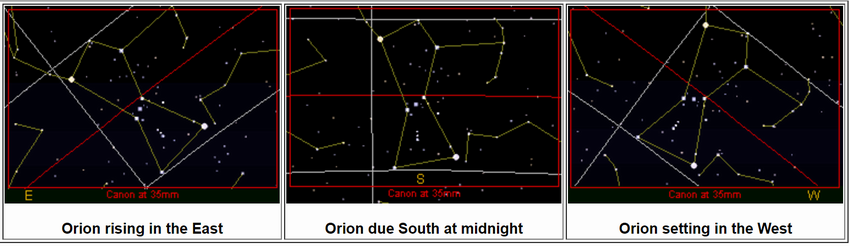
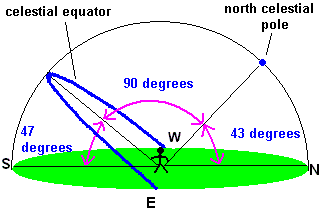
Each will be given a camera, which will be set level with his/her horizon, pointing due east, and will photograph the rising full moon just as it clears the horizon. When we compare the three photos, we will find that as compared with that of the observer at the equator, the moon's disc in the northern observer's photo will appear to have been rotated 45° clockwise with respect to the horizon, and vice versa in that of the southern observer.

Using the globe model, it is easy to visualize why this is by imagining a single video camera affixed to a train car that travels between the northern and southern observers; were this train to travel around 3000 miles per second, here is roughly what the film would show:

​

Unlike the globe model, the flat model can provide no coherent explanation for this apparent rotation, which can be confirmed by anyone, anywhere, with no special training or equipment.

Also worth mentioning is that a single observer can confirm this independently, from one single position, since over the course of the night, his longitude will travel through 180°. Were the earth instead to stand still, we could use a similar train to more easily visualize the movement of his camera; in this case, it travels from his evening position at 45°N, up over the north pole, to his morning position at 45°N on the opposite longitude. Just as with the previous example, he will observe an apparent 90° rotation of the moon over this time, albeit clockwise, as opposed to what is shown above for the south-bound train.

Furthermore, note that these observations clarify not only the apparent rotation of the moon, but also lay bare in precisely which way the "two people looking at a figure on the ceiling" explanation misleads: by neglecting the fact that frame of reference matters.

Provided that we take the hook, we may not notice the fact that when looking at the ceiling, we are free to rotate our view to produce any result we like; if we wish the two views to be mutually inverted, as suggested by Benji, we need only make sure to set the up vector of each camera opposite that of the other. And if we wish them to match, we need only align the camera up vectors; it is a perfect confirmation bias trap.

However, we are no longer free to make this mistake, once the horizon enters the picture; instead, since we then see that the rotation is occurring with respect to the horizon itself, and that it would be futile to attempt to get round it by rotating the camera, it becomes inescapable that either:

1. Each observer sees a custom-rotated version of the moon, or
   
2. Each observer's horizon is rotated with respect to the moon.

Whereas the latter is simply self-evident in the globe model, the former cannot be explained, irrespective of the model, by anything but the purest solipsism.

 

[Z.W. Wolf]

Thanks for the post. In the case of the single observer watching the moon seemingly rotate during the night, this effect has a name: field rotation.

Everything in the sky "rotates" during the night. It might be easier to visualize a constellation like Orion rather than the moon. In the northern hemisphere, Orion is in the southern sky and looks (more or less) like this.




Orion is on the celestial equator and this is what he looks like with the celestial equator marked in red.




If you're not familiar with the celestial equator, first imagine in this illustration that the CE is a bicycle tire and the line from the north pole is the axle. The tire rotates from east to west. Now imagine this is a line on a clear plastic sphere. The sphere is rotating around the earth. That's the celestial sphere.


Apropos to our issue of field rotation, imagine the celestial equator as a line across the night sky. Point to the east (your left) and draw your finger across the southern sky along that line all the way to the west (your right). Now imagine holding a model of Orion in your hand and make the same movement. It's easy see why Orion makes this seeming clockwise movement.

Or just try it in the room you're sitting in. Hold your right hand out in front of your left shoulder with the thumb down. (You're looking at the back of your hand.) Move your arm in a wiping motion to your right. You'll end up with your thumb pointing up.

If you're on the earth's equator (perhaps in Ecuador), Orion comes up due east, passes straight over head and sets due west. His bow comes up first and goes down first. Easy. What comes up first goes down first. (Try the hand trick again, but this time wipe your hand directly over your head to see what I mean.)

Getting back to the moon, it shouldn't be surprising that a rising moon, in the northern hemisphere, looks like this:



And a setting moon looks like this:



You can see that it has "rotated" in the same direction (clockwise), and pretty much to the same degree that Orion rotates.

But of course the moon doesn't actually rotate like this. We are moving with the earth's surface and it's our point of view that changes. Much like looking at something from a merry-go-round.

 

[Z.W. Wolf]

To help people who aren't too familiar with the terms we've been using here, this old Air Force instructional film is the best thing I've found. The celestial equator is defined at 4:18 for instance, but I think you should start at the beginning.

The great circle perpendicular to the axis is called the celestial equator... It is an extension of the earth's equator.

Content from External Source

One correction. Only the stars were thought to be on the celestial sphere. The planets, the moon and sun were thought to have their own spheres inside the celestial sphere. We still use the abstract concept of the celestial sphere.

 

[Fajar]

I have a question regarding to the moon rotation. Standard science says that moon is circling the earth every 30 days, so basically every month moon will alyas be in between earth and sun.

My question, why we don't experiencing solar eclipse every month? I'm not saying that it should be a total eclipse, since the theory says the moon’s orbit is inclined to Earth’s orbit by about 5 degrees. But some part of earth should be covered by moon's shadow during the daylight (partial solar eclipse). Can anyone explain this?
Thanks

 

[Landru]

I have a question regarding to the moon rotation. Standard science says that moon is circling the earth every 30 days, so basically every month moon will alyas be in between earth and sun.

My question, why we don't experiencing solar eclipse every month? I'm not saying that it should be a total eclipse, since the theory says the moon’s orbit is inclined to Earth’s orbit by about 5 degrees. But some part of earth should be covered by moon's shadow during the daylight (partial solar eclipse). Can anyone explain this?
Thanks

A lunar eclipse occurs when the Moon enters the Earth's shadow. A solareclipse occurs when the Moon's shadow falls on the Earth. They do not happen every month because the Earth's orbit around the sun is not in the same plane as the Moon's orbit around the Earth.

Content from External Source

http://curious.astro.cornell.edu/ab...-do-we-not-have-eclipses-every-month-beginner

I simply asked your question in Google. In the future you should start by doing that.

 

[Trailblazer]

since the theory says the moon’s orbit is inclined to Earth’s orbit by about 5 degrees.

5 degrees may not sound very much, but when you consider how small the moon is and how far away from the Earth it is, it's quite a lot.

The diameter of the moon is a little over 2,000 miles, but it is 240,000 miles away, in other words it is over 100 times further away than it is wide.

It's easy to forget that, because diagrams of the Earth and Moon often show them much closer together than they really are. In actual fact they don't look like this:



but like this:




So you can see that the angle doesn't have to be very much at all for the shadow to miss the Earth entirely. (In fact the angular diameter of the moon as seen from the Earth is only about half of one degree.)

 

[0x90]

Considering it from the sun's point of view, the thing that might strike one as incredible is that eclipses happen as frequently as they do:

 

[ZoRay]

Sorry MineBen but you haven't given this much thought.

If you and I are standing face to face (you are looking north and I am looking south) on a level surface in a room and look above at an assymetrical object centered directly between us, what you see as the top pointing south, I will see as the bottom pointing south and vice versa.

Try it. Do some experiments.

Science is based upon the scientific method; if you can't produce a working model of your theory, it has to be discarded.

 

[rumbleh]

So, after looking into some flat earth claims that where the Arctic Circle lies proves the FE, I came across an excellent piece of information that is easy to understand yet undoubtedly deals a blow to the Flat Earth theory.

It's quite simple: the moon appears upside down in the Southern Hemisphere compared to the Northern hemisphere.

This cannot be explained on a flat Earth.

Looking at blue and red pins on earth's surface, I presume that is the height of observer.

Try to do the same drawing, using a real scale person. The lines will be drawned over the earth.

 

[Trailblazer]

Looking at blue and red pins on earth's surface, I presume that is the height of observer.

Try to do the same drawing, using a real scale person. The lines will be drawned over the earth.

Your drawings are not anything like to scale. The moon is about a quarter of the diameter of the Earth, and 30 Earth diameters away from it.



We're talking about observers in the northern and southern hemispheres, not right at the north and south poles as in your diagram. You can easily see the moon from both northern and southern hemispheres at the same time.

 

[David Ridlen]

...

This video shows why a spherical moon circling above a flat earth cannot work. ...

Here also is a video of how a flat moon would appear circling above flat world-
Source: https://www.youtube.com/watch?v=bQDGCjHPCn0

 

[Alan Steffens]

Unfortunately it's so ludicrous that I feel it's not worth debunking. Who seriously gives this explanation?

I feel this way about the entire subject of flat earth.

Honestly, if someone's grasp of scientific concepts is so poor already, what makes us think that we can change their mind by offering further scientific explanations?

[...]

 

[Whitebeard]

I feel this way about the entire subject of flat earth.

Honestly, if someone's grasp of scientific concepts is so poor already, what makes us think that we can change their mind by offering further scientific explanations?

[...]

Its not really a case of changing the minds of the hard core flat earthers. More a case of pointing out their errors, mistakes and - lets be honest about this - lies, so that others don't follow them into the rabbit hole.

 

[David Ridlen]

...what makes us think that we can change their mind by offering further scientific explanations?

[...]

FE is associated with a steadily growing anti-'gubment' trend, equating science with corporate conspiracy/brainwashing among the poorly educated. My FE debunk vids do receive occasional "thank you! I/my sister/etc was getting sucked into this' comments from people on the fence. Solid threads, videos or comments will be conveniently linked in various discussions, so the same point is not typed out repeatedly.

Belligerent fundamentalists may resist all reason. But a less rigid mind may change over time in the face of accumulated logical points they eventually admit to themselves they cannot refute.