SPOILER ALERT: This will seem totally mental to all but amateur geometry geeks who like pointless puzzles (and maybe them too).
So I've been playing some more with the idea of left-right curves, etc, and seeing what happens if we 'isolate' the 'different curves' by making the earth a cylinder. First off, there's the left-to-right cylinder, like this:
And then the head-on cylinder, like this:
In the attached spreadsheet you can generate what the curve of a line of towers would look like for these two cylinders, as well as the sphere and the flat earth, for a variable viewer height and variable height of towers. Like, for a viewer at 100 feet looking at a line of towers 100 feet high - nearest tower 4 miles away; furthest tower 8 miles from that, perpendicular to the viewer - the curves of the 4 different models look like this:

What's interesting about this is that for the first couple of miles the sphere curve and the head-on cylinder curve are similar, as are the left-to-right cylinder and the flat earth, whereas by the end they've flipped, as can be more clearly visualised here:
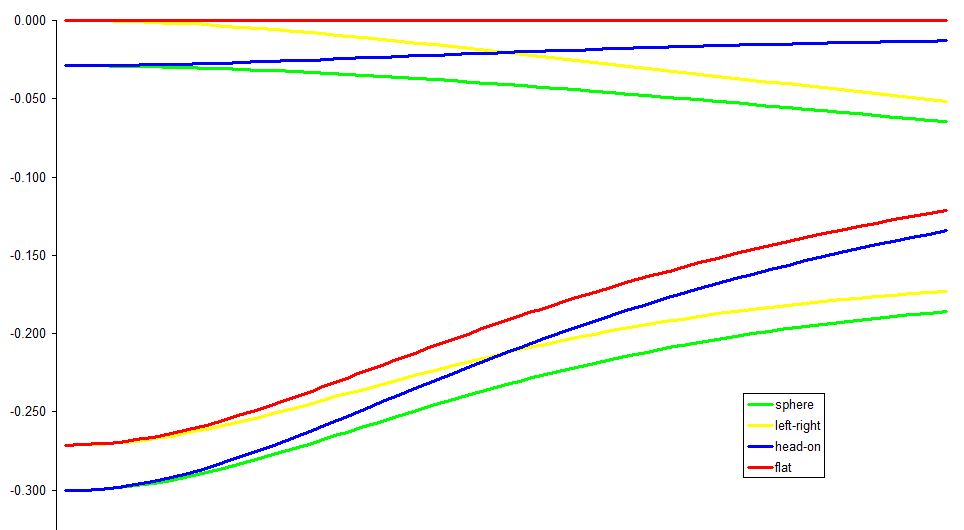
(Top lines tops of towers; bottom lines the bases.)
And making the line of towers 25 miles long changes the picture again:

This illustrates that the left-to-right cylinder is closest to the sphere earth, in the overall shape of the curve - though I'm not really sure what it illustrates about our ideas that we can see 'different curves' here on the actual earth.
Probably that we were wrong all along: there's just CURVE, and the only way we'd see a 'left-to-right curve' would be if we were tens of thousands of miles away in space and gigantic enormous towers about 50-miles high were lined up across the 'top' of the globe over a span of a thousand miles or so - and even then we'd still be seeing 'the curve of the horizon'.
Note: all this is assuming I've got the geometry more or less correct, which I'm not quite 100% sure on. For one thing, there's a weird kink in the curve between the 1st and 2nd points that I can't figure out. For another, I was expecting the flat earth tower bases to form a straight line, given that, as far as I can tell, it's only perspective playing a part in that one.
Seem pretty much right though. Perhaps some other puzzle-lovin' freak can iron out any creases in the 'quations.


