I find this all fascinating, and I'm glad to see I'm not the only one pondering this concept. I guess the possibility of seeing this 'left-to-curve' is something that has always been assumed, on both sides, but just that it was too difficult to see. After all, isn't it the basis for the famous B.O.B. question?

Mostly when I'd seen people address this they'd used equations based on a sagitta or bulge, and pointed out that it's too small to see (as well as the obvious fact of the terrain, etc) - but now we're questioning the notion of it.
On the one hand, it's clear that the line of the towers in the image in the OP is curved because of distance and hidden amount. But what if we remove hidden amount? Ie, raise the viewer elevation high enough so that the towers are all nearer than the horizon, and are therefore only considering those within the blue scrawls:
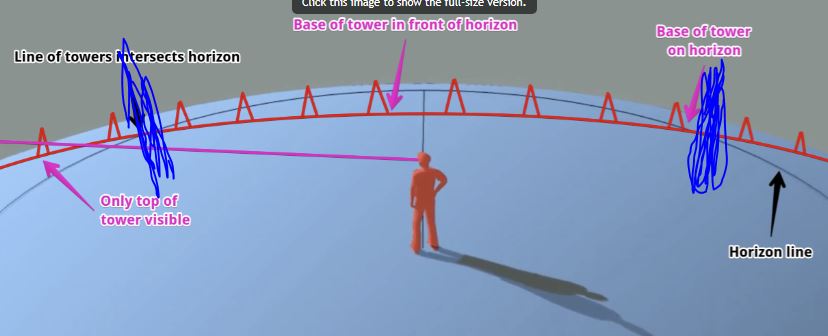
In one sense, the viewer is 'disembodied' - the eyes are floating in 3D space; the line of sight doesn't depend on the ground between him and the towers, and we could 'cut away' the earth so that all we had was a 3959-mile radius flat, vertical circle with a line of towers running across its rim. I believe this is what Soundly meant by "the towers project a great circle", and in that sense, what we'd be looking at would be the left-to-right curve. But, at the same time, the outer towers also appear 'smaller' because of perspective, while the eyes are 'raised' because of the head-on curve.
I think I go back to my earlier idea: the reason the towers appear lower in the OP image is a combination of perspective, head-on curve, hidden amount, and left-to-right curve.
If we raise the viewer's eye level to 50 feet, we eliminate hidden amount.
If we raise the viewer's eye level to the height of the towers, and consider
only the tops of the towers, we eliminate perspective, as the flat earth view shows all the tower tops would be at eye level.
Now, to eliminate the head-on curve, I'm trying to imagine the earth as a 3959-mile radius cylinder. On the one hand, this feels like it works, being as it 'drops' the viewer height to the surface of the cylinder, so that when he's looking at the closest tower, at 4 miles, he's now 10.7 feet lower in 3D space than he was on the sphere. Or, in degrees, for a 100-foot high camera, looking at the base of a 100-foot high tower, he's looking down at 0.271°, whereas the sphere earth viewer is looking down at 0.3°.
Similarly, when looking at the tower 8 miles from the closest tower, the angle on the cylinder is 0.173°, while on the sphere it's 0.186°.
I'm not quite sure yet what the difference between the two angles signifies.
Apologies: I know I'm fumbling here, and extrapolating way more from the OP than was ever intended. It's like an itch what needs scratching. A riddle and a puzzle. I feel I may be close, or I may be barking up completely the wrong tree. No doubt superior minds will clarify.
PS Anybody know how tall the towers are? And how far above the water the camera was?

