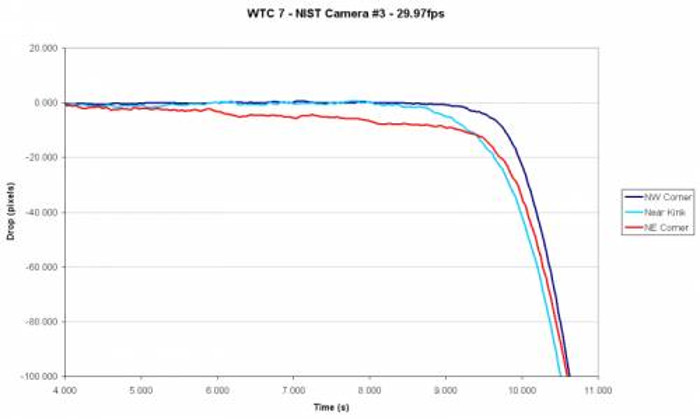
The collapse of WTC7 is something that convinces people that 9/11 must have been some kind of complex inside job, with the building rigged with explosives set to go off after the planes hopefully hit somewhere and fires burned for hours.
Assuming this is a plausible plan for the sake of discussion, what is it about the collapse of WTC7 that is so suspicious? Well it does (unlike WTC1 & WTC2) actually look like a a controlled demolition - the building falls more or less straight down into a cloud of dust, unlike WTC1/2 where the clouds of dust started near the top of the building. But perhaps the most compelling aspect for many people is the fact that it fell so fast, and that for a portion of the collapse the acceleration of the building was indistinguishable from freefall.
Have a look at this video so you can see what I am talking about
Source: https://www.youtube.com/watch?v=nqbUkThGlCo
NIST explains it like this.
https://www.nist.gov/el/faqs-nist-wtc-7-investigation
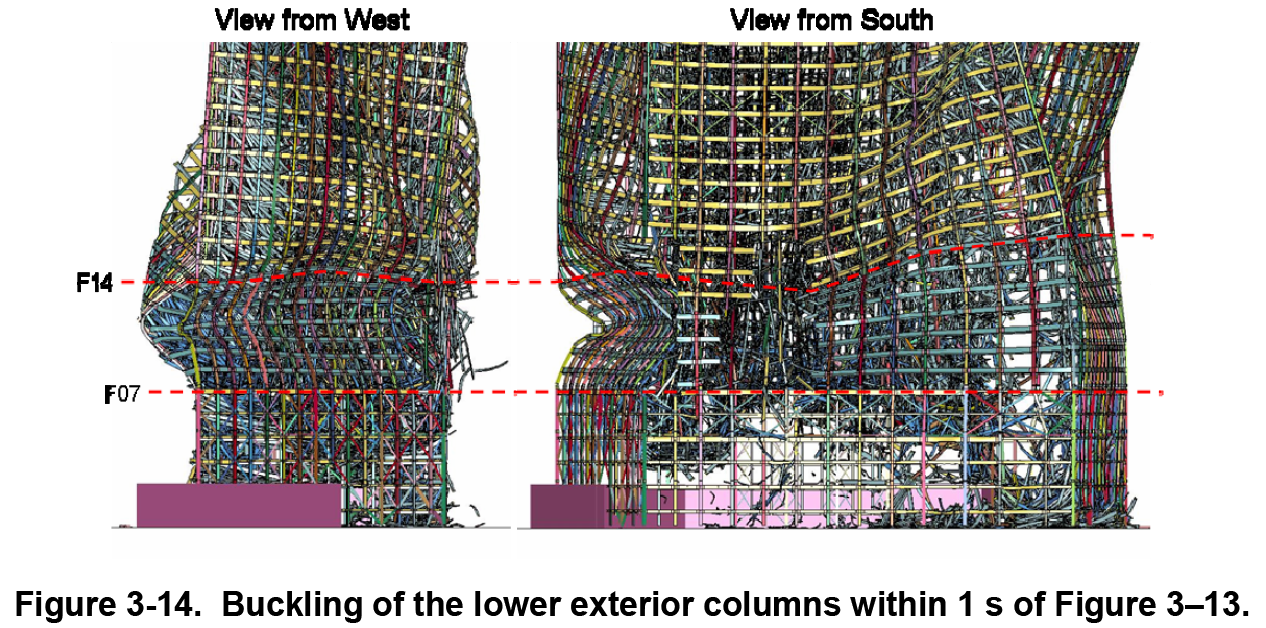
So there you are, negligible support from the structure below because the exterior columns buckled and lost their capacity to support the loads from the structure above. Here's the type of buckling I am talking about (although this is during stage 1).
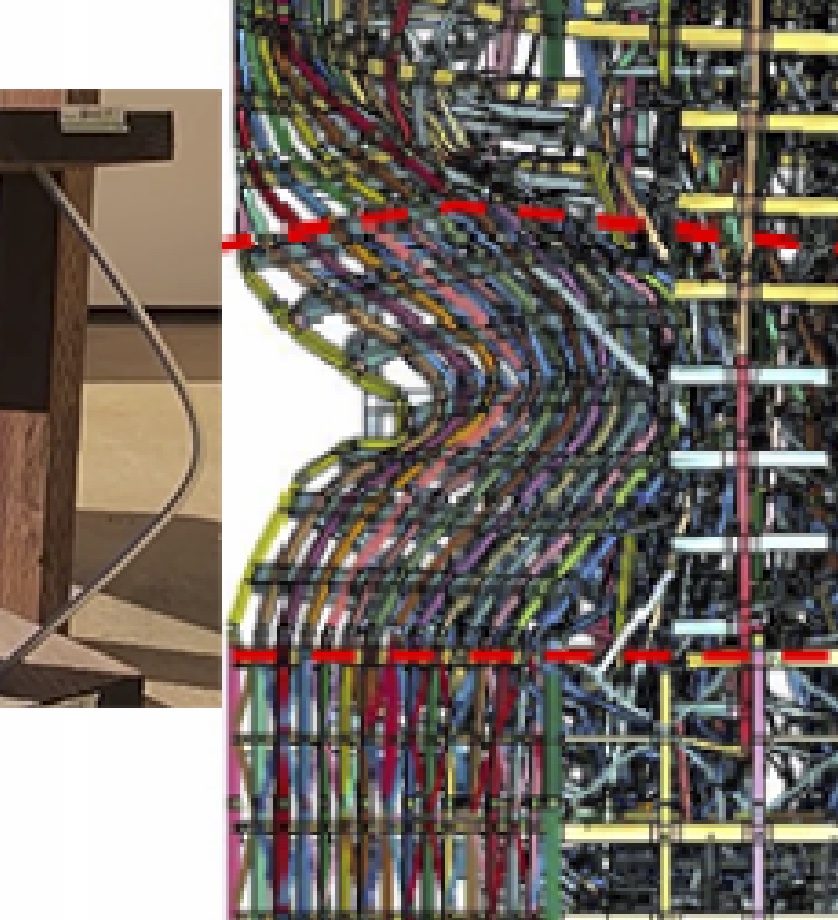
And look at that in perspective. The building is actually a lot taller than it appears in the video, and the above image only shows the bottom. See where the actually is relative to the top and it makes a lot more sense.

The problem here is that it does not make sense to people. Even if the columns buckled, wouldn't they still provide some resistance? Well yes, but the key question here is how much resistance. If they provide a force equal to the mass they support times g, then the mass they support will not move. If they provide a force equal to 1% of the mass times g, then the mass will move down with an acceleration of 99% of g (i.e. negligible resistance, and essentially free fall).
Columns of a building can support a static load of a low multiple of the mass above them before failing. Conservatively you can use 2x. So put very simply if the support of a column was to be reduced so that the mass it previously supported were to fall at 99% of g, then the supporting strength of the column would have to be reduced by a factor of 200.
And this happens when a tall column or wall loses its support and buckles.
Notice is does not mean zero support. If a column could support 1000 tons, and it's degraded by a factor of 200 then than means it can still support 5 tons. However while the column is buckling the 1000 tons it was supporting will fall at an acceleration of 99% of g.
You can demonstrate the principle here with a soda can. Soda cans are very strong. In fact an empty soda can will support over 4,000 times its own weight. I tested an empty soda can, and it supported 130 pounds before failing at just above that weight. The can weighs 0.03 pounds (about 14 grams)

I then took another can of the same type and, like with WTC7, I removed the structural support. I cut the top and bottom of the can and flattened the sheet of metal into a single wall. I then tested how much weight it supported.

It was less than half a pound. The exact same piece of metal that previously supported 130 pounds was now supporting less than half a pound. Over 200x reduction in supporting strength. This means that if you put the amount of weight that it could previously support above this structurally unsound piece of metal, it would fall at over 99% the rate of acceleration of g.
And that's what happened with WTC7 during those 2.25 seconds of "free fall". The columns below had buckled, and offered negligible resistance. Still tons of resistance, but compared to the mass they previously supported, it was practically nothing. Hence 99% freefall.
Source: https://youtu.be/jjoHaXrm_u4
This experiment was inspired by the following Facebook discussion:
https://www.facebook.com/groups/286311730249/permalink/10154622005660250/
[UPDATE]
I've done a couple of buckling experiments over the last few days:
Source: https://www.youtube.com/watch?v=SSMc_7NEkgk
(Shows the effect of bracing on the critical load of a column)
Source: https://www.youtube.com/watch?v=zjuINfpItxE
(Shows rapid onset of buckling)
[Update Feb 13 2018]
The above is largely concerned with the collapse of the exterior of the building. However it should be noted that all of the interior columns also failed by buckling before the exterior of the building buckled.
Here's a rough overlay of the core columns on the full NIST simulation visualization at the same point in time (22.5 seconds into the simulation)
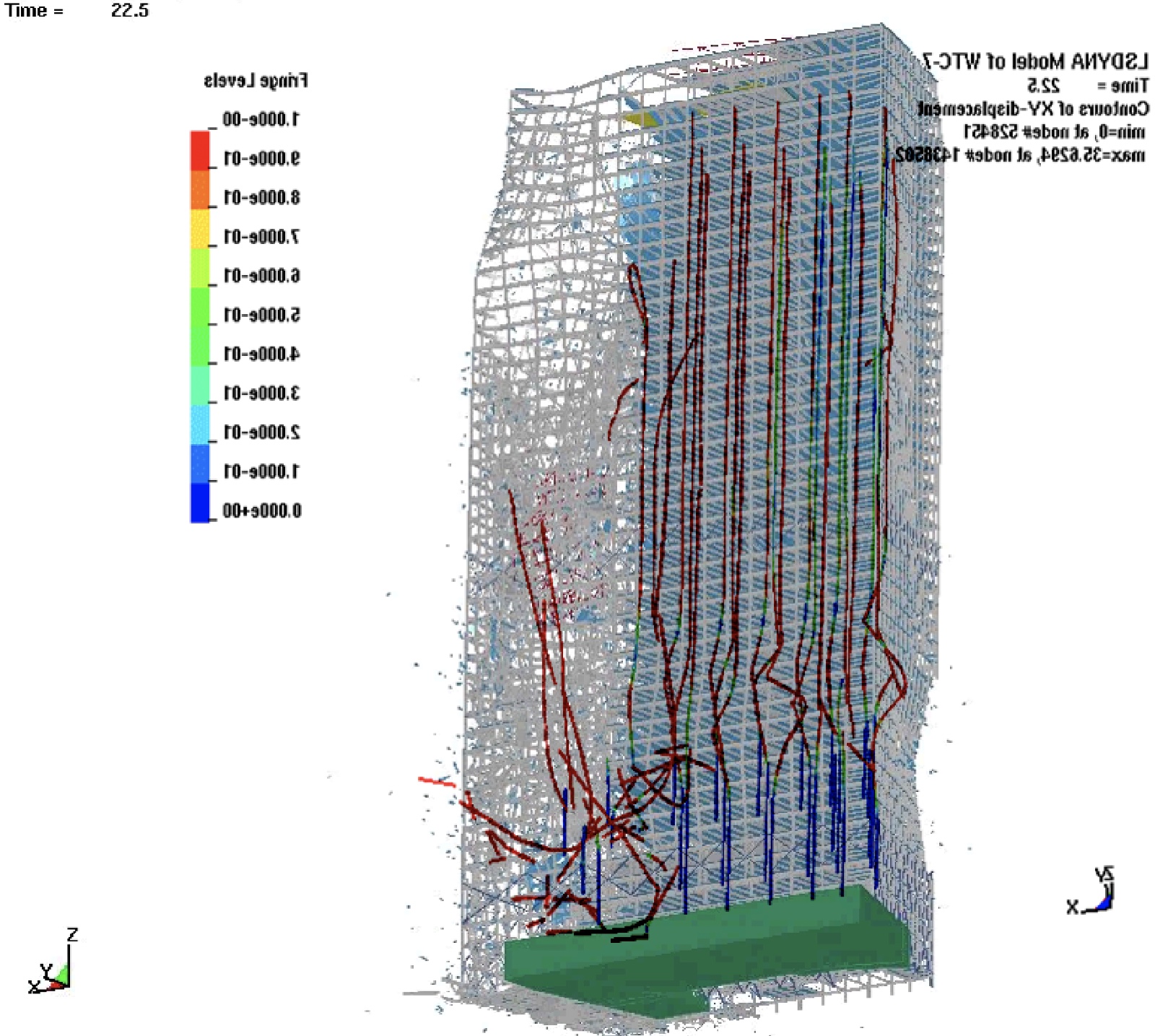
The exterior columns are just starting to buckle at this point, but the interior columns have all failed.
Assuming this is a plausible plan for the sake of discussion, what is it about the collapse of WTC7 that is so suspicious? Well it does (unlike WTC1 & WTC2) actually look like a a controlled demolition - the building falls more or less straight down into a cloud of dust, unlike WTC1/2 where the clouds of dust started near the top of the building. But perhaps the most compelling aspect for many people is the fact that it fell so fast, and that for a portion of the collapse the acceleration of the building was indistinguishable from freefall.
Have a look at this video so you can see what I am talking about
Source: https://www.youtube.com/watch?v=nqbUkThGlCo
NIST explains it like this.
https://www.nist.gov/el/faqs-nist-wtc-7-investigation
(emphasis mine)
The approach taken by NIST is summarized in NIST NCSTAR Report 1A, Section 3.6, and detailed in NIST NCSTAR Report 1-9, Section 12.5.3.
The analyses of the video (both the estimation of the instant the roofline began to descend and the calculated velocity and acceleration of a point on the roofline) revealed three distinct stages characterizing the 5.4 seconds of collapse:
This analysis showed that the 40 percent longer descent time—compared to the 3.9 second free fall time—was due primarily to Stage 1, which corresponded to the buckling of the exterior columns in the lower stories of the north face. During Stage 2, the north face descended essentially in free fall, indicating negligible support from the structure below. This is consistent with the structural analysis model, which showed the exterior columns buckling and losing their capacity to support the loads from the structure above. In Stage 3, the acceleration decreased as the upper portion of the north face encountered increased resistance from the collapsed structure and the debris pile below.
- Stage 1 (0 to 1.75 seconds): acceleration less than that of gravity (i.e., slower than free fall).
- Stage 2 (1.75 to 4.0 seconds): gravitational acceleration (free fall)
- Stage 3 (4.0 to 5.4 seconds): decreased acceleration, again less than that of gravity
So there you are, negligible support from the structure below because the exterior columns buckled and lost their capacity to support the loads from the structure above. Here's the type of buckling I am talking about (although this is during stage 1).
And look at that in perspective. The building is actually a lot taller than it appears in the video, and the above image only shows the bottom. See where the actually is relative to the top and it makes a lot more sense.
The problem here is that it does not make sense to people. Even if the columns buckled, wouldn't they still provide some resistance? Well yes, but the key question here is how much resistance. If they provide a force equal to the mass they support times g, then the mass they support will not move. If they provide a force equal to 1% of the mass times g, then the mass will move down with an acceleration of 99% of g (i.e. negligible resistance, and essentially free fall).
Columns of a building can support a static load of a low multiple of the mass above them before failing. Conservatively you can use 2x. So put very simply if the support of a column was to be reduced so that the mass it previously supported were to fall at 99% of g, then the supporting strength of the column would have to be reduced by a factor of 200.
And this happens when a tall column or wall loses its support and buckles.
Notice is does not mean zero support. If a column could support 1000 tons, and it's degraded by a factor of 200 then than means it can still support 5 tons. However while the column is buckling the 1000 tons it was supporting will fall at an acceleration of 99% of g.
You can demonstrate the principle here with a soda can. Soda cans are very strong. In fact an empty soda can will support over 4,000 times its own weight. I tested an empty soda can, and it supported 130 pounds before failing at just above that weight. The can weighs 0.03 pounds (about 14 grams)
I then took another can of the same type and, like with WTC7, I removed the structural support. I cut the top and bottom of the can and flattened the sheet of metal into a single wall. I then tested how much weight it supported.
It was less than half a pound. The exact same piece of metal that previously supported 130 pounds was now supporting less than half a pound. Over 200x reduction in supporting strength. This means that if you put the amount of weight that it could previously support above this structurally unsound piece of metal, it would fall at over 99% the rate of acceleration of g.
And that's what happened with WTC7 during those 2.25 seconds of "free fall". The columns below had buckled, and offered negligible resistance. Still tons of resistance, but compared to the mass they previously supported, it was practically nothing. Hence 99% freefall.
Source: https://youtu.be/jjoHaXrm_u4
This experiment was inspired by the following Facebook discussion:
https://www.facebook.com/groups/286311730249/permalink/10154622005660250/
[UPDATE]
I've done a couple of buckling experiments over the last few days:
Source: https://www.youtube.com/watch?v=SSMc_7NEkgk
(Shows the effect of bracing on the critical load of a column)
Source: https://www.youtube.com/watch?v=zjuINfpItxE
(Shows rapid onset of buckling)
[Update Feb 13 2018]
The above is largely concerned with the collapse of the exterior of the building. However it should be noted that all of the interior columns also failed by buckling before the exterior of the building buckled.
Here's a rough overlay of the core columns on the full NIST simulation visualization at the same point in time (22.5 seconds into the simulation)
The exterior columns are just starting to buckle at this point, but the interior columns have all failed.
Last edited: