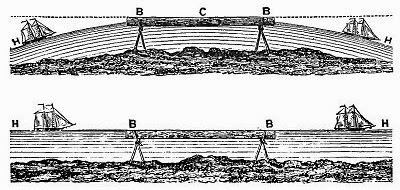
You might want to test for the dip of the horizon instead. This would test the FE claim that "the horizon is always at eye level." By which they mean to say the earth must be a flat plain rather than a sphere.
You already have a good spirit level. Set up a sheet of Masonite on saw horses perfectly parallel with the ground. Stand behind the level board and lower your eye until you are looking along the top of the board - your line of sight is perfectly parallel to the ground you are standing on.
You won't be able to see the horizon. The horizon will be below your line of sight.
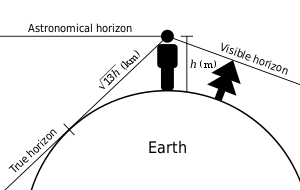
You will be looking at what's called the "astronomical horizon." You've set up the board perpendicular to a line from the center of the earth to the zenith.
The true horizon is the plane that touches the surface of the earth perpendicular to the radius of the earth.
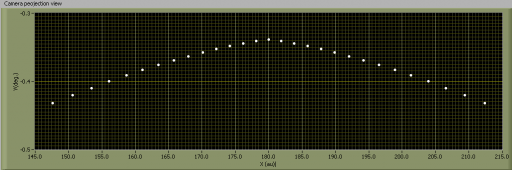
The flat earth claim that "the horizon is always at eye level" is muddled and untrue. What they probably are trying to say is: If your line of sight is perfectly parallel to the ground you are standing on, the horizon is always level with your line of sight. It's impossible to know that your eyes are in that position, of course, especially since the ground you stand on is uneven. They simply look at the horizon, and of course it's in the middle of their field of vision, therefore it's at eye level. They even claim this is true when looking at photos.
But it's untrue anyway. The dip of the horizon has been known about and studied for at least a thousand years.
The astronomical horizon would be the same as the true horizon on a very large or infinite disk earth. But here on the sphere earth they are not the same. The difference is the dip of the horizon, and the dip increases with observer altitude.
As matter of fact an 11th century Persian astronomer measured the dip of the horizon from sea level and from the top of a mountain and used that difference to calculate the radius of the earth.
https://en.wikipedia.org/wiki/History_of_geodesy#Al-Biruni
There has been some skepticism about the accuracy of his findings because Al-Biruni didn't know about Snell's law.
Complication:
The geographic horizon is the boundary between earth and sky - in your case the boundary between sea and sky. (Confusingly the boundary between sea and sky is often called the true horizon, as opposed to a cluttered horizon you get on land.) The geographic horizon is not exactly the same as the true horizon because the earth has an atmosphere. Even in standard-atmosphere conditions refraction makes the geographic horizon somewhat lower than the true horizon. When there are steep temperature gradients in the atmosphere, refraction can really play tricks with the geographic horizon.