Jedo
Member
Well I guess in answering how the buckling leads to free fall (back on-topic) we have to look a bit more in detail into the basics of buckling.
I've been researching about the theory of buckling and of structural stability the last days, since I have had not much of an idea of it. However, I already learned some things.
When you measure the maximum load you have to account correctly for the boundary conditions i.e. the way the ends of are column are fixed (or not), see (from Wikipedia)
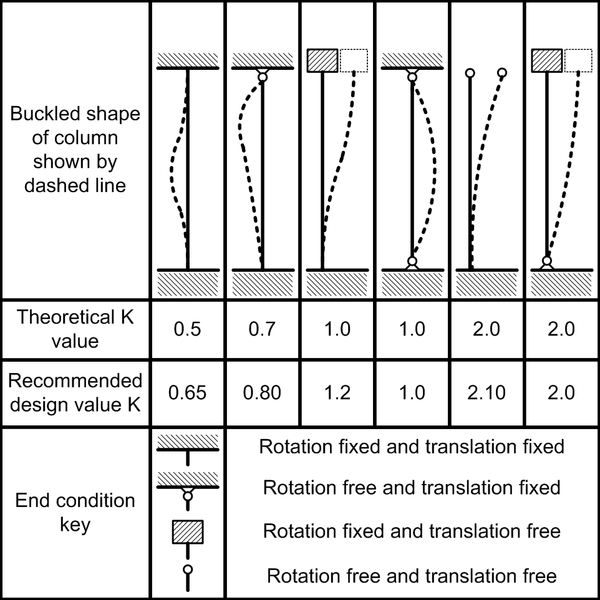
@Mick West measured the fourth case, where the buckle mode has the form of x =x_0 \sin(\pi z / L) (sorry for tex source code here, but the latex feature seems broken). In the building of WTC7 the columns are all fixed, so this corresponds to the first case with fixed ends where the buckle mode takes the form x= x_0/2 (1 + \cos(2\pi z/L ). The sinus and cosinus come from the fact that it is a second order differential equation.
The critical buckling load then should be 4 times as big, as it is proportional to 1/(KL)^2.
Furthermore, when you look not at the total load but on the stress, you get that it is proportional to the ratio of the moment of inertia to the total cross section area, I/A. So the beam @Mick West used had two very different moments of inertia, and it buckled along the axis with the smaller moment of inertia. Such a beam is called a slender beam.
From Wikipedia:
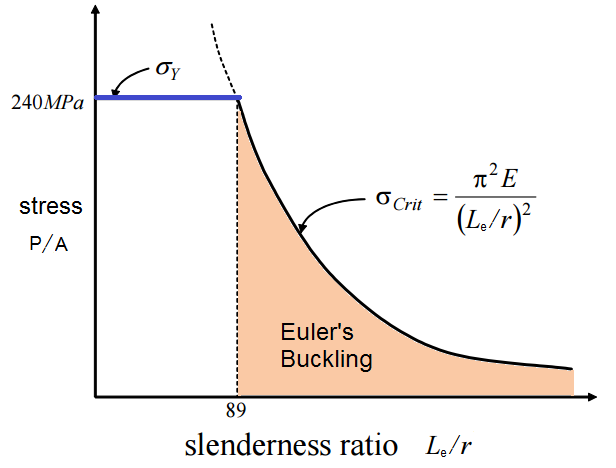
However, close to the border between the yellow and white area, there is apparently another failure mode, which is given by Johnson's parabolic formula, which gives another boundary by a parabola:
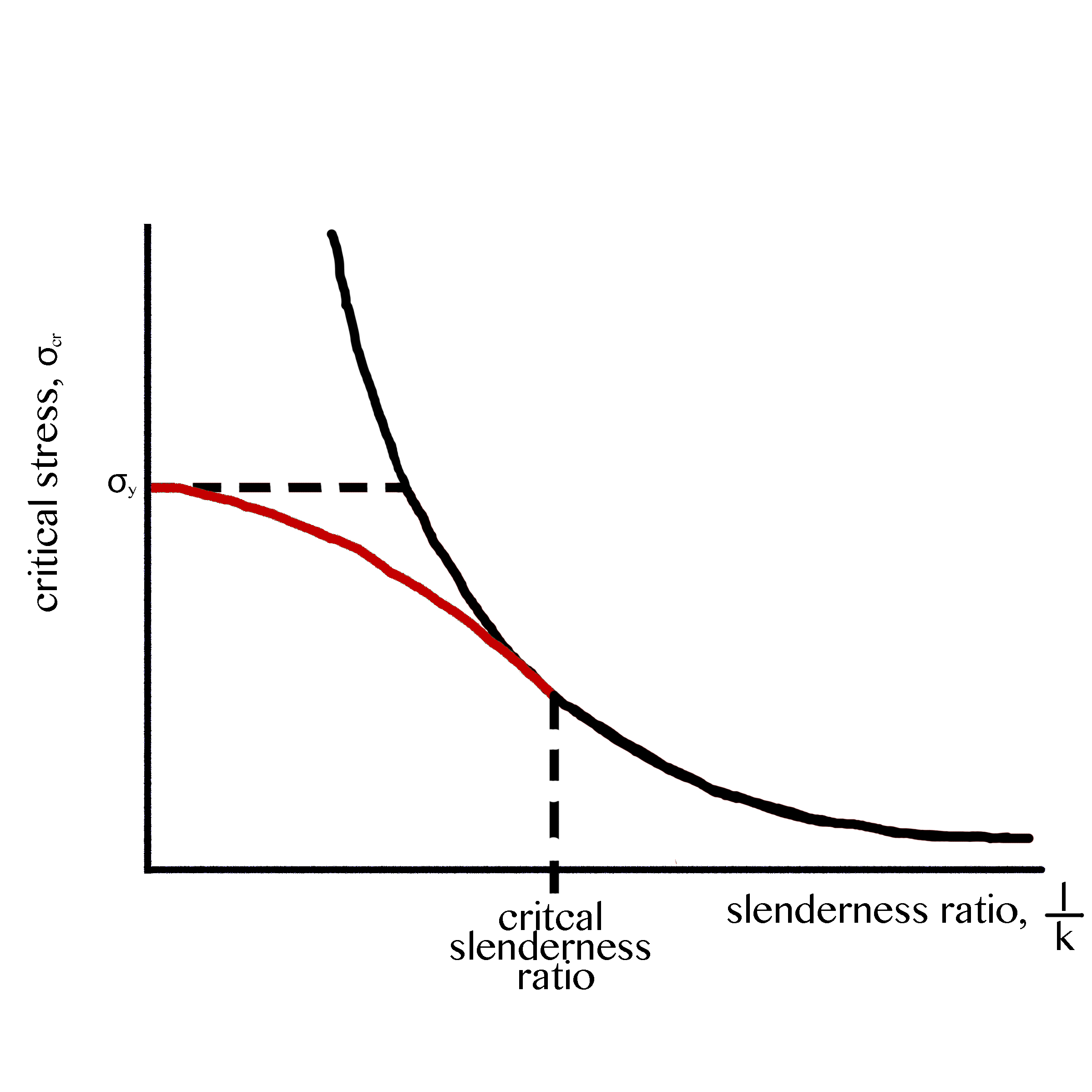
I did however not get how they can calculate this critical slenderness ratio, nor what failure mode exactly this corresponds to. I would have guessed that this is a inelastic buckling mode, as the critical stress is the yield for axial compression only. Maybe someone can help here?
With this much bowing the bar supports just 12 pounds. How would I have to brace it so that it supports 1200 pounds? Theoretically I don't need to use multiple supports, I can just use an 8" section braced at either end and that should be the same as the longer piece braced every 8"?
I've been researching about the theory of buckling and of structural stability the last days, since I have had not much of an idea of it. However, I already learned some things.
When you measure the maximum load you have to account correctly for the boundary conditions i.e. the way the ends of are column are fixed (or not), see (from Wikipedia)

@Mick West measured the fourth case, where the buckle mode has the form of x =x_0 \sin(\pi z / L) (sorry for tex source code here, but the latex feature seems broken). In the building of WTC7 the columns are all fixed, so this corresponds to the first case with fixed ends where the buckle mode takes the form x= x_0/2 (1 + \cos(2\pi z/L ). The sinus and cosinus come from the fact that it is a second order differential equation.
The critical buckling load then should be 4 times as big, as it is proportional to 1/(KL)^2.
Furthermore, when you look not at the total load but on the stress, you get that it is proportional to the ratio of the moment of inertia to the total cross section area, I/A. So the beam @Mick West used had two very different moments of inertia, and it buckled along the axis with the smaller moment of inertia. Such a beam is called a slender beam.
From Wikipedia:
So Euler buckling (i.e. elastic) is valid only for high slenderness ratios before it yields, here the yellow areaFor slender columns, critical stress is usually lower than yield stress, and in the elastic range. A stocky column would, on the contrast, have a critical buckling stress higher than the yield, i.e. it yields in shortening prior the virtual elastic buckling onset.

However, close to the border between the yellow and white area, there is apparently another failure mode, which is given by Johnson's parabolic formula, which gives another boundary by a parabola:

I did however not get how they can calculate this critical slenderness ratio, nor what failure mode exactly this corresponds to. I would have guessed that this is a inelastic buckling mode, as the critical stress is the yield for axial compression only. Maybe someone can help here?
Last edited: