Yes, sighting both horizons at once could be interesting. I had thought of doing it with a device called a "line ranger", as seen on page 8 of "Principles and Use of Surveying Instruments" Third Edition 1969. A line ranger is just two mirrors at a 90deg angle so that you can see two opposite directions at once, perpendicular to your line of sight, so that you can see if you are exactly on a straight line between two points. I had thought that flat earth investigators could even make their own very cheaply and simply, and even calibrate it themselves, so they could verify themselves that it was accurate. But then I realized that it would be hard to find a place near the coast of California that I could view the ocean from a high mountain with ocean in both directions 180deg apart. Plus I realized that even a relatively simple construction project could be a significant obstacle. I couldn't readily find suppliers for these line rangers. Probably because of the insufficiently specific search words "line" and "ranger", and because surveyors probably use them less in todays world of GPS surveying.
Then I realized that a tube level might work well. I'm clearly not the first to think of that. One small obstacle there is getting the clear tubing. A solution could be to use a garden hose. A garden hose would allow a nice long baseline for very precise leveling. Unfortunately it doesn't make for easy photography of the water surfaces with the horizon. I was thinking of just filling the hose completely to each end. One issue there is that the hoses all seem to have a loose metal thread ring on the female end that might leak if filled all the way. But it seems workable, and probably nearly all flat earth investigators have, or could borrow, a hose. I was thinking of sticking a couple short pieces of clear tubing into the ends of the garden hose, but who would happen to have pieces of just the right size? Maybe we could improvise some clear end pieces, like say by wrapping some clear packing tape around the ends of the hose, or hot gluing some water bottles to the ends.
Viewing out opposite windows of an airliner would be great. The altitude would give a large angle. There are a couple issues I can see. One is that it may be hard to keep the straight edge level between viewing from one side and the next. One solution to that might be to set up two cameras, one at each end facing opposite directions. Then you could edit the two videos or pictures together to show a simultaneous view and reduce the doubts that flat earthers might have about the stability of the straight edge. Each camera would tend to block the view of the other, so you might have to set each up along two different parallel straight edges, and make calibration images before and after. Another possibility might be to put a camera at one end of the straight edge, and a mirror next to the other end.
Another tougher problem might be that the flat earthers might blame the horizon droop angle on refraction through the tilted/curved airline windows.
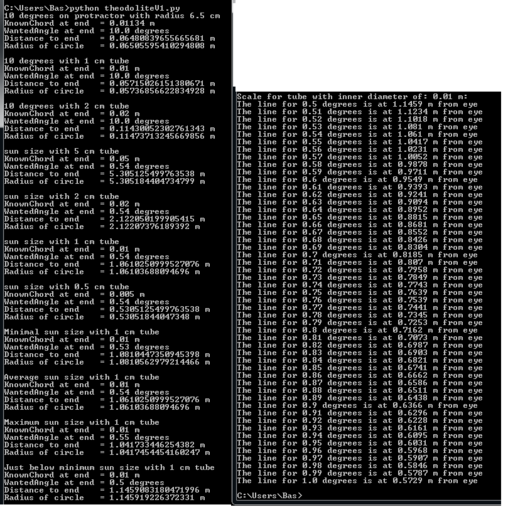
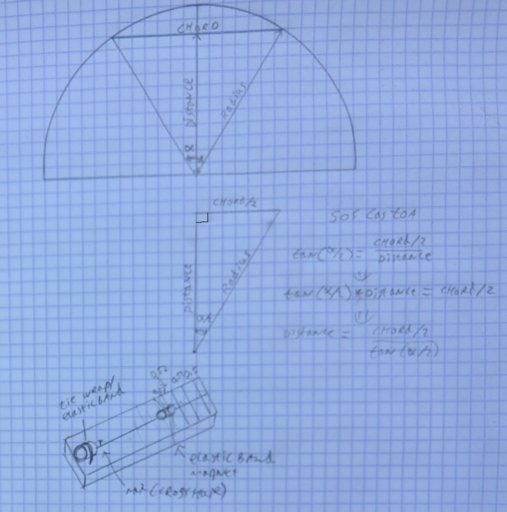
@Bas Koning - Your device looks like it might be interesting, but the blue graph paper image is a little too blurry for me to make out what's shown, even when I enlarge it. As far as graduating an angle measuring device is concerned, one trick is to use a linear scale, such as a centimeter ruler or tape. For example, if you mount a couple centimeters of a centimeter ruler, 57.3cm away from the location of the eye, then for small angles, the centimeters will represent full degrees and the millimeters will represent 1/10 of a degree, or 6 minutes of angle. Another idea for measuring angles with a little accuracy over a wider range, is the CD jewel case sextant like this:
http://www.tecepe.com.br/nav/CDSextantProject.htm
Unfortunately I would say it's not usable to look at the sun without a proper professional sun shade, not a homemade one. But that still leaves a lot of other things one can measure. The cool thing about sextants is that you can do accurate angle measurements just hand held, without a stable mount, because both images of the two objects being viewed move together when you wobble the sextant.
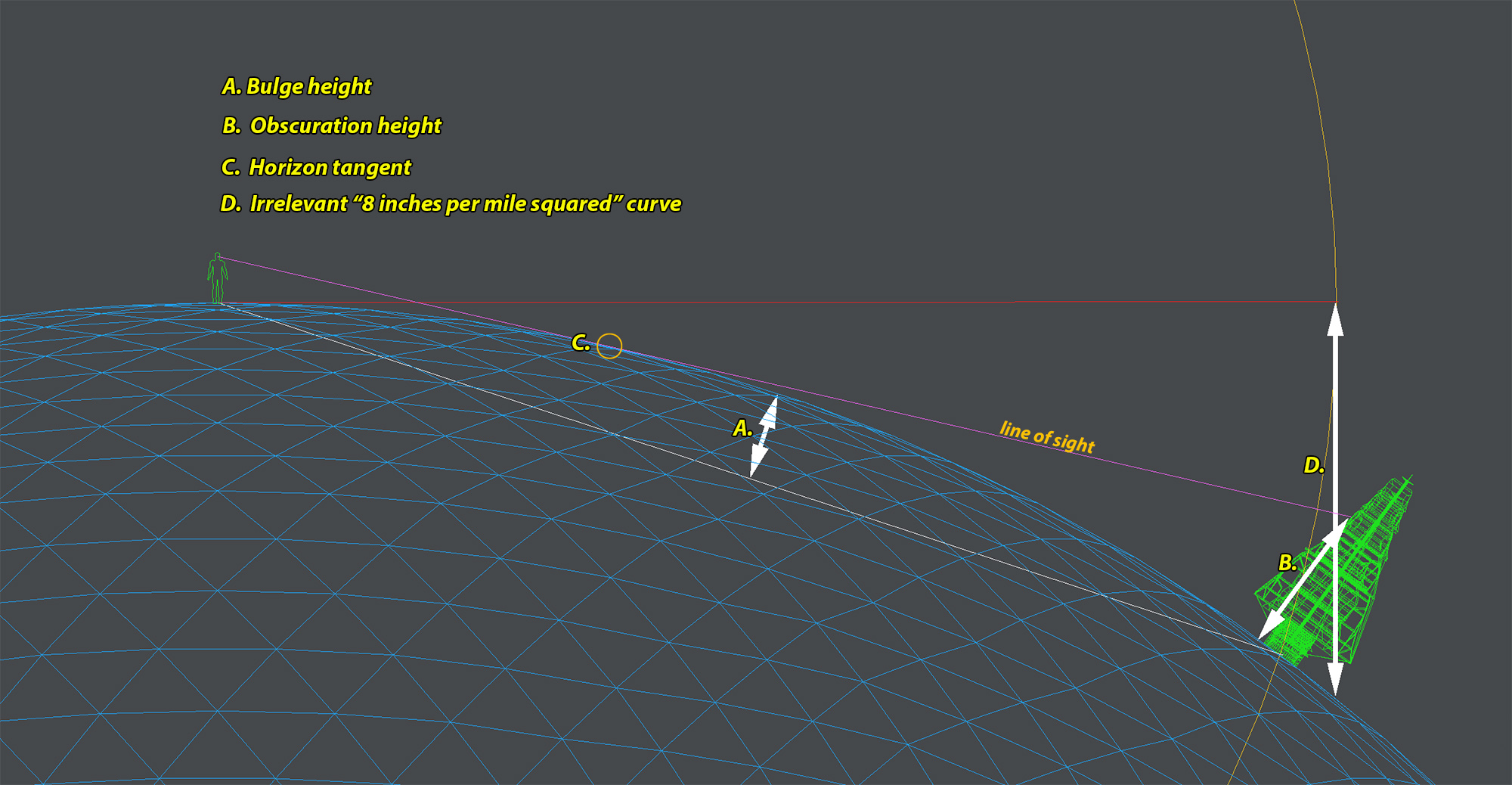
@Everyone - A great time to catch these tube level images would be at sunrise/sunset or moonrise/moonset, so that the actual horizon level could be more accurately seen, and also so that a sense of scale for the droop angle would be in the frame. Unfortunately ,it usually gets foggy by sunset around here. Also, the sun cuts through horizon haze better, but it creates camera exposure and possible eye damage complications. Remember, even if the haze has cut the visible sun brightness to a comfortable level, that may not mean that the invisible longer infrared and shorter ultraviolet wavelengths may not still be getting through at dangerous levels. You can't feel the burn from the invisible wavelengths. And just because you or others have looked at it before doesn't mean that it didn't or won't cause just a little eye damage, like maybe slightly degrading your night vision or something that you don't immediately notice. I would however be willing to risk my low end camera sensor pointing at a dim sun near the horizon. For photographing the full brightness sun, I cut a pair of polycarbonate sun glasses up into seven pieces to stack in front of my camera lens. At first I thought that would be tolerably good for naked eye viewing as well, then I realized that although the polycarbonate might block all the UV, the pigments might not block the long infrared wavelengths well at all.