I am saying the points made here by OneWhiteEye about when the 20% elongation and fracture occur are not legitimate.
Do you think you could bother to say why? On the previous page you said:
ASTM A36 is a very ductile steel and requires about 20% elongation before fracture.
But when I unequivocally show
100% elongation of elements in your partner's FEA, that property of steel is magically waived and somehow my points are not legitimate. Surely you can explain that.
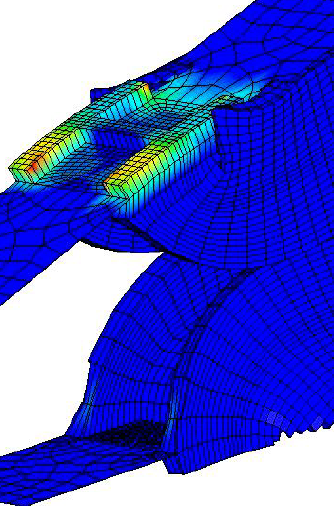
Attached is another WTC structural member with 180 degree bending. No fractures are observed.
You aren't looking very closely. Maybe it will be more obvious from the other side:

You can't get anything right, can you?
I'm perfectly aware of that specific column, I can even dredge up much better examples than that, and in pictures big enough to see!
I did so for psikeyhacker who, like you, seemed unable to come up with more than two examples on his own. But, as I pointed out to him, for every one mangled column you can find, I'll find a hundred that are barely deformed.
I think OneWhiteEye needs to show us his/her calculations for the energy dissipation during buckling of a floor of columns at about the 97th floor of the North Tower, since he/she is claiming that the energy calculations in the paper by Gregory Szuladzinski, Richard Johns, and I are not accurate.
You are so clueless. Your value of η doesn't come from a calculation at all! It comes from an FEA. Not analytic derivation, not laboratory experiment - an FEA, done by one guy and cited by no one except himself. The SHS FEA, not the three hinge FEA.
Somehow I doubt we will see any calculations and will not hold my breath.
1) I don't have to do my own calculations to show the flaws in your work.
2) You've got a fair bit of nerve challenging me about calculations, given
our first encounter when I corrected you on your initial dismal foray into basic mechanics.
3) Long before you figured out the right formula to use for three-hinge buckling,
I latched on to it courtesy of Bazant. Here it is:
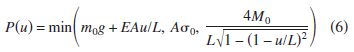
4) There's nothing hard about that formula; arithmetic and square root. Read on from that point to see how I implemented a linear approximation of it in a physics simulation.
5) The energy dissipation calculated in three-hinge buckling is a purely academic exercise; it did not happen (you still haven't found one example of it).
6) But I can do it again, if you insist.
When one uses the load displacement relation of Bazant and Cedolin, it's immediately apparent that being scaled to
mg as it is, one only need determine the Maxwell line for equivalent force as a fraction of peak capacity or imposed load. There's no need to evaluate that function every time a number is needed. For Bazant's estimates, it's about 15% of peak and about 38% of
mg. So, 0.38mgh. There, that wasn't hard.