Use of Scale Model or Full Sized models for investigating 9/11 collapses

[jaydeehess]

Obviously, how far the destruction must continue through the floors is among the more significant aspects of what a model could establish.

Or, one can note there is no apparent mechanism by which such a progression could be arrested and thus no requirement to model it. That is exactly what NIST concluded and thus they did not create an fea for the approx 100 more floors.

 

[Keith Beachy]

I can make a simplified model out of paper, cardboard and an elastic band to show in principle that an aeroplane can fly. That's easy for me. I want a simplified model of the Towers that can be shown in principle to destroy itself under the dynamic momentum of a falling upper section. That's apparently impossible for you.

A model like this? The WTC towers collapse is a real experiment, it is called an event; reality. Fire and gravity collapse, twice. It meets all the stuff you want, all your requirements. Reproducibility and Validation

The towers were not weak. What is the point of a model for the collapse?

http://www.structuremag.org/article.aspx?articleID=453
http://www.structuremag.org/Archives/2007-3/D-Spotlight-ComputerModeling-Mar07.pdf

What do you want to model?

 

[Mick West]

Thinking about the problems of scale illustrates why the Heiwa challenge is meaningless. He calls for a homogenous structure, with the top 1/10th being dropped on it to crush the lower 1/10th.

You are requested to describe a structure where a small top part C can crush the much bigger bottom part A from above, when top part C is dropped by gravity on bottom part A.

The structure with parts C and A can look like the structure right or below, e.g. a square block of any material/elements (e.g. steel or wood floors and pillars or whatever) connected together plus plenty of air between the elements! All elements and joints of the structure must evidently be weak and break easily! The total structure can have any mass or density, e.g. density 0.25 (kg/cm3) or 250 (kg/m3), i.e. light, like the WTC towers that were mostly air ... like a bale of cotton.

The top part C is the 1/10th top of the total structure! It has mass M kilograms (kg)! M can be 1 kg or 100 000 000 kg! It does not matter.

The drop height is max 3.7 meters!

The bottom part A is the 9/10th bottom of the total structure. It has mass 9 M kilograms. It means A is 9 times bigger than C!

When top part C with mass M impacts bottom part A from above after a free fall drop of 3.7 meters by gravity (g = 9.82 m/s²), it applies 36.334 M Joule energy to the (total) structure with mass 10 M.

Will bottom part A with mass 9 M be crushed into rubble by top part C with mass M? Can 3.63 Joule energy initiate a collapse destruction of 1 kilogram of A?

That's the Challenge! The Anders Björkman Challenge! According US authorities incl. US presidents of all kinds, security advisors, agencies, experts, universities and plenty idiots of all types it happens all the time! Little weak, top C (with density 0.25) crushes big strong, bottom A (with same density 0.25), i.e. the one layer C top part crushes, POUFF, POUFF, the nine layers of bottom A, one after the other, into rubble (with density 1)!

The problem is that if you have something at a scale of 1/200th, then you need to have non load-bearing elements account for 1/199th of the total mass of the structure. The only way you could do that would be incredibly heavy flat plates on a rigid gossamer lattice of columns and bracing beams.

 

[Mick West]

Here's a very abstract two story model with something resembling the scale we are talking about. The soda cans are empty, the weights are 30 pounds each.

 

[Mick West]

And here's what happens when you drop another 30 pound weight on it:

(parts of image masked for file size, full video attached)

 

[Keith Beachy]

And here's what happens when you drop another 30 pound weight on it:

(parts of image masked for file size, full video attached)

Nice model. I could not get the eggs to stand still.

ROBERTSON: —This is a very robust floor system, rather different from that portrayed in the British press, but in any event—the other issue having to do with the failure mechanism, again, I've not performed an in-depth study on the matter, but I carried the event far enough along so that I became convinced that if you dropped the floors above onto the floors below, i.e., caused a collapse in the middle of the building some place, that without question, the collapse would continue, right down to the foundations. There's no way that the structure below would be able to carry, let us say 14 floors. Not possible, not even close to being possible.
And it would not be a slow failure either; drop 14 floors on any one floor of that building and it would collapse instantly. Well, no, not "instantly"; that's a bad term. It would collapse ins—instantly as far as you or I would be able to perceive it.

From the structural engineer for the WTC, who did not ask for a new model, he built two full up models.

 

[deirdre]

Here's a very abstract two story model with something resembling the scale we are talking about. The soda cans are empty, the weights are 30 pounds each.

so the weights are the concrete floors?

 

[Mick West]

so the weights are the concrete floors?

Essentially yes - but more the weight of the columns and the floors, scaled. At small scale, the columns (the cans) have to be very light compared to the load they are supporting.

 

[Mick West]

You know, I think it would be possible to make a 6' scale model that would approximate the collapse progression. You'd need to use material that were 1/200th the strength, however since the girders generally retained their shape, then you'd just need to model weak splices every 3 floors. So I was thinking the column would be square dowels of wood, with the splices just being masking tape. Toothpicks or straws for floor seats, then a mixture of royal icing and #12 lead shot for the concrete (and to bump up the weight) - just spread it over paper in a tray to create slabs. A little glue on the seats to hold everything together.

Probably better to just make a model of the top half of the tower, so you can just go to 1/100th, more manageable. It will still demonstrate the principle - the bottom half is just an extension. Still be darn fiddly though.

There's way too many variables (and other scale factors not accounted for), but perhaps you could at least demonstrate the principle, and get Haiwa's $1,000,000

I'd still do it on a computer first.

 

[Cube Radio]

What's interesting about your two storey model, Mick, is how the mass of the falling "floors" quickly moves away from the perpendicular as it drops. This problem is evident also in the two storey model presented by the MIT professor that Jazzy was such a fan of. If the model was extended a little in terms of height and levels and the collapse proceeded as it does in your video there would quickly be very little mass falling directly over the base of the structure and the collapse would be arrested.

I agree that it seems as though building a model that reproduces the principle of the "total destruction effect" that allegedly destroyed the towers ought to be simple. But of course the fragile columns into which you suggest a heavy weight could be dropped must be progressively stronger as you move down the structure, to support the equally heavy "floors" that are between those you are dropping and the ground.

Psikeyhakr's model was built to be as weak as possible: so weak, in fact, that it did not have vertical stability and needed a central column, not part of the experiment, to help hold it upright (and also held 100% of the falling mass over the base). However it effectively demonstrates that if you add just a few more "floors" than the two levels you have represented in your model, the collapse cannot progress to the ground.

Incidentally, if you are going to invoke Haiwa and his million dollars, perhaps you should unban him so that he can speak for himself.

 

[jaydeehess]

Essentially yes - but more the weight of the columns and the floors, scaled. At small scale, the columns (the cans) have to be very light compared to the load they are supporting.

Ok, but as I keep harping on about, the Heiwa scenario and so many other models out there try to model column failure by overloading. Thus they continually point out how much bigger the lower columns were than the upper columns and declare that they would have arrested the collapse.

The strength of the columns was bypassed/made irrelevant, by removal of their lateral support, the floor trusses between core and perimeter.

 

[jaydeehess]

Psikeyhakr's model was built to be as weak as possible: so weak, in fact, that it did not have vertical stability and needed a central column, not part of the experiment, to help hold it upright (and also held 100% of the falling mass over the base). However it effectively demonstrates that if you add just a few more "floors" than the two levels you have represented in your model, the collapse cannot progress to the ground.

.

,,, and as pointed out by me a few times now, Psikey is modeling the crush buckling of vertical support. Ok fine, such a model indicates collapse arrest. Now all he needs to do is find a collapse that supposedly happened by direct vertical overloading of columns. That would not apply to the WTC towers though.

At collapse initiation, at that very moment, the columns of the upper block could not possibly be aligned with the same columns of the lower block. If they were then it would not collapse.
Simple huh?
So by what mechanism would anyone propose that the dynamic forces of the falling mass be transfered to the columns? Answer, only that small portion of mass actually hitting the columns would be affected by the columns. that's a tiny percentage of the forces being generated. where does the bulk of that mass fall, upon what does the dynamic forces impinge? The floor space , both that in the core and the outer, office space.

So, why does Psikeyhacker model column buckling and purport that it models what happened in the towers? Its either misunderstanding of what actually took place, or its sophistry.

 

[Mick West]

What's interesting about your two storey model, Mick, is how the mass of the falling "floors" quickly moves away from the perpendicular as it drops. This problem is evident also in the two storey model presented by the MIT professor that Jazzy was such a fan of. If the model was extended a little in terms of height and levels and the collapse proceeded as it does in your video there would quickly be very little mass falling directly over the base of the structure and the collapse would be arrested.

But that's a problem of scale. If you can't get past that, then there's no point proceeding, so perhaps we should just focus on that?

 

[deirdre]

What's interesting about your two storey model, Mick, is how the mass of the falling "floors" quickly moves away from the perpendicular as it drops.

the WTC wasn't made from dumbbells and coke cans.

 

[Mick West]

Psikeyhakr's model was built to be as weak as possible: so weak, in fact, that it did not have vertical stability and needed a central column, not part of the experiment, to help hold it upright (and also held 100% of the falling mass over the base). However it effectively demonstrates that if you add just a few more "floors" than the two levels you have represented in your model, the collapse cannot progress to the ground.

This model?

What do you think this demonstrates? The floors in the WTC do not support each other, they maintain the vertical stability of the columns and the outer walls. He's added an infinitely strong vertical stabilizer, and infinitely strong floors.

It might be an interesting exercise to scale that model UP to 1,000 feet. How would that work?

 

[Mick West]

Here's something more along the lines of what I was thinking:

Now this has significant problems. However it's illustrating the basic construction of inner and outer supports tied together with long span floors. If the floors fail, then the columns lose their horizontal stabilization, and so will fail. The outer walls will mostly fall outwards, the inner core will stand longer as it is stronger, but will eventually collapse.

The model is not too useful as it stands, but imagine if it were taller, and you dropped a mass of floors onto it:

 

[Mick West]

 

[Mick West]

The model is two dimensional. I built it against an inclined plane (about 15° from vertical) to constrain it to a plane.

There are obviously still vast problems of scale here. The columns had splices every three floor for one, the floor connections are incredibly strong, the floors are overly elastic, and all the weights are off. But I think it begins to illustrates the principle of a wave of rubble removing floors, and the columns failing at the splices.

 

[jaydeehess]

BTW, Mick, its interesting what occured to the upper soda can. Gee, only vertical forces involved. You must have been off screen and firing a bullet into that can just as it was crushed. That's the only way that it could be ejected with such force. But I digress.

Your Jenga model is very close to what I proposed earlier, except in my thought experiment the columns were single solid units with cardboard floors on peg on the columns. In that way the columns would be massively overbuilt, simply would never buckle in the experiment, yet the whole thing will fall apart when the floors are taken out.

The integrity of the columns are irrelevant in such a collapse mode.

 

[Mick West]

Mark II, using "seated" connections made of tape:

Added some supports at the base to stop them sliding out:

Dropped the upper mass on it

Floors fail before columns:

 

[Mick West]

 

[Cube Radio]

Impressed by the time you've taken build even this, Mick. Are you aware of the computer model built by femr2? I'll see if I can find the link when I'm home from work.

 

[WeedWhacker]

Impressed by the time you've taken build even this, Mick. Are you aware of the computer model built by femr2? I'll see if I can find the link when I'm home from work.

I appreciate your response to the effort of Mick's.

But yet in reading through this thread, I find your whole "point" hard to discern. Seems there is, on your 'side', a reluctance to accept the way that the WTC Towers fell (from damage and gravity).

However, what seems the "elephant in the room" (missing) is your alternative "explanation".

 

[deirdre]

I appreciate your response to the effort of Mick's.

But yet in reading through this thread, I find your whole "point" hard to discern. Seems there is, on your 'side', a reluctance to accept the way that the WTC Towers fell (from damage and gravity).

However, what seems the "elephant in the room" (missing) is your alternative "explanation".

i think this thread is Only for scale models. ten bucks Mick is at Home Depot buying window screen for the sides of the towers. (PS @Cube Radio , can we bypass the 'dust' by just making the weight 50% less? <surely 50% didn't float out of the building right? and would make a small scale physical model much easier to replicate [ish])

 

[Cube Radio]

My basic point is that there has been no successful attempt to model the most structurally and politically significant collapses in history, either physically or virtually, in the decade plus since they occurred.

 

[deirdre]

@WeedWhacker how much does a plane weigh with and without fuel?

 

[deirdre]

My basic point is that there has been no successful attempt to model

you mean PHYSICALLY model. right?

 

[Cube Radio]

To my knowledge there is also no physically accurate computer model of the collapse sequence in existence. I'm not even sure if basic information that would make this possible, such as the precise distribution of steel and concrete through the towers (obviously they were stronger lower down) is available in the public domain.

 

[WeedWhacker]

@WeedWhacker how much does a plane weigh with and without fuel?

Depends on the airplane.

A little Cessna 150/152 (for example) has a maximum gross weight of 1,600 pounds (IIRC). So, the empty airplane is (roughly) about 1,100 pounds. Also, this thing holds about 19 gallons of fuel, each wing. (Avgas weighs 6 pounds per gallon).

{These are things that ALL pilots who are beginning to learn, must know}.

NOW....when we get into larger airplanes, well....we get into bigger weights, and more complication as a result.

For example, the Boeing 757 (which I am quite familiar with) has variations in models (the -200 versus the -300) and different engines that can be ordered, by the buyers (Pratt & Whitney or Rolls Royce, e.g.).

For a B-757-200 the maximum gross takeoff weight is (typically) 240,000 to 255,000 pounds. Generally, the 'empty' weight is (IIRC) about 127,000 - 129,000 pounds (but again, this will vary extensively, per specific airplane, and type).

 

[Mick West]

My basic point is that there has been no successful attempt to model the most structurally and politically significant collapses in history, either physically or virtually, in the decade plus since they occurred.

My questions are: why would there be? and: what would that look like?

Consider, there are two possibilities here.

A) The collapse was from the impact damage and the fires
B) The collapse was aided in some way, like with explosives

Now from my perspective, option A seems by far the most obvious. There seems nothing at all to indicate option B is true, and all the objections to option A boil down to "looks odd to me", or rather specious misapplications of models and statements like "violating Newton's laws".

I feel my opinion is shared by the vast majority of the worlds structural engineers, scientists and physicists. Once the collapse started, then total collapse was inevitable.

So from my perspective, the ONLY reason to make a model is to explain things to people who think it looks wierd. Now as I debunker I like explaining things, hence spend 30 minutes making that model earlier. But there seems to be no good reason to spend $1 Million to make a model JUST so things can be explained.

Tell me, what exactly would satisfy you? What would it look like?

 

[Jason]

Mark II, using "seated" connections made of tape:

Added some supports at the base to stop them sliding out:

Dropped the upper mass on it

Floors fail before columns:

I'm curious to see what would happen if the center colums were taped together to give the core columns more strength.

 

[Mick West]

I'm curious to see what would happen if the center colums were taped together to give the core columns more strength.

It probably would remain standing, like the "spire". I would need more floors before it fell from instability.

The model also needs splices between the column segments. Now the scale errors start to magnify, as the strength ratios and failure modes are very different to full size.

 

[jaydeehess]

That is uncannily similar to what I have been saying all along. Looks like the only reason the column on the right did not fail is that one 'floor' did not tear away from it and acted as a diagonal brace to the center column section.

 

[Mick West]

That is uncannily similar to what I have been saying all along. Looks like the only reason the column on the right did not fail is that one 'floor' did not tear away from it and acted as a diagonal brace to the center column section.

Yes, that's exactly what happened - and remember the entire thing is leaning back against a wooden board. the extra friction adds stability.

 

[Jason]

It probably would remain standing, like the "spire". I would need more floors before it fell from instability.

The model also needs splices between the column segments. Now the scale errors start to magnify, as the strength ratios and failure modes are very different to full size.

Now the floors had a 700 Pa floor design allowable, each floor should have been able to support approximately 1,300 t beyond its own weight, what were the loads for the core columns? Also

the thickness of the plates and grade of structural stell varied over the height of the tower, ranging from 36,000 to 100,000 pounds per square inch (260 to 670 MPa). The strength of the steel and thickness of the steel plates decreased with height because they were required to support lesser amounts of building mass on higher floors.

I think this is also important since the planes impacted the buildings at the upper levels, but I rarely ever hear this discussed. But I'm curious to know what loads the core columns were able to take

 

[Mick West]

So here I added splices to the center column. Two "splice plates" tying them together horizontally and vertically.

center column remained standing, just.

 

[Mick West]

Now the floors had a 700 Pa floor design allowable, each floor should have been able to support approximately 1,300 t beyond its own weight

Remember that static load is vastly different to dynamic load. An empty soda can will support 100 pounds just resting on it. But it will fail if you drop a 2 pound weight on it from six feet up.

 

[jaydeehess]

Remember that static load is vastly different to dynamic load. An empty soda can will support 100 pounds just resting on it. But it will fail if you drop a 2 pound weight on it from six feet up.

Yes, and that is another issue, along with the irrelevance of the strength of the core columns, that seems to be vastly misunderstood. People have talked about how the bathroom scale jumps way up as you step on it, and that is a good model of dynamic force.

The way I like to illustrate it is to tell someone to place a 3/4" steel nut on their head. One can barely feel it there if you have a good head of hair. Now, have a partner drop said 3/4" steel nut onto your head from 2 feet above. NOW, you can feel it, hair, no hair, or anything short of a 8 inch thick Afro. If you are adventurous, have it dropped from 8 feet above your head. Having band-aids on hand might be in order.


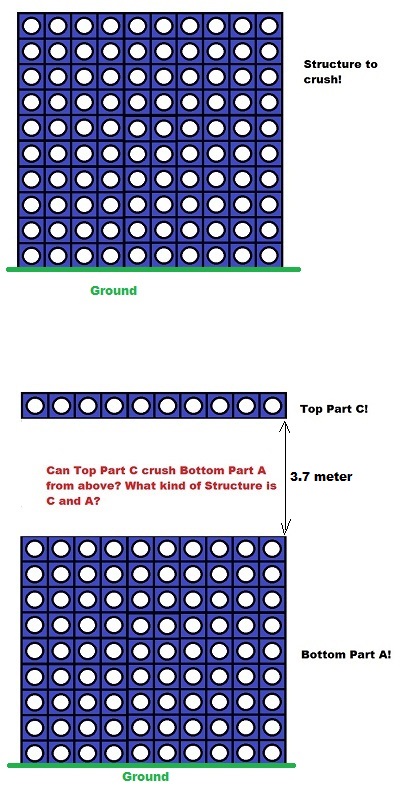
As for the floor's ability to take a load; Shall we assume a tenfold safety margin? If we then assume that each floor above initial collapse was the same we already have ten times the floor ability to transfer a load to the columns. Add in the weight of the upper storey's columns, and you easily at the very least match the max floor load. BUT, this mass is doing two things. First, its moving, and thus as it hits it generates a dynamic load. It has come down a distance of approx 3.7 meters at something above 0.6g. This alone would overwhelm the floor. If that's all that is happening its bowing the floor trusses to max, cracking concrete due to the flexure, and pulling on the attachments to the columns at either end of the trusses.

That's an approximation of reality because of other, more random effects in play. One obvious effect is that the column sections that have failed will reach the next floor down, first. They will punch through the floor like a hot needle through butter (to paraphrase a metaphor). Where will they do this? Not in the center of the floor pan. The column punch through will occur somewhere near the column section of the lower 'block'. In that vicinity are the truss seats and inter-core beams. This will be minor compared to the soon to follow bulk of the upper mass contacting the floor but it serves to illustrate that this next floor down is not in pristine condition when it gets smacked.

As this first lower floor is impacted, the falling mass is also buffeting the core columns, imagine how the core columns sway as the building reacts to wind in normal circumstances. Now the core columns at the collapse zone are reacting to this buffeting in similar fashion except that they are not all moving in the same direction at the same time. Its more random/chaotic.

Approximations of what's happening are just that, approximations. They take into account the more gross features of the collapse sequence. The more random features result in things such as the so called 'squibs' ahead of the visible collapse zone.

So, the thread topic, modeling. We can model some modes of collapse, we have to make approximations to do so. We also have to try to take into account scaling issues. What we cannot take into account are the more random effects.

In Mick's soda can/dumbell example above we saw one can get ejected horizontally at quite a rate. According to a strict mathematical modeling that would not have occured. a small random effect caused an off center load on the can, it buckled on one side first and was then pushed laterally by the still falling weight. In this case it illustrated a concept that the model was not specifically designed to illustrate.

Modeling, and more to the point, interrpretation of the results of modeling, is as much an art as it is a strict technical endevour.


but that's just me rambling...

 

[Jason]

As for the floor's ability to take a load; Shall we assume a tenfold safety margin? If we then assume that each floor above initial collapse was the same we already have ten times the floor ability to transfer a load to the columns. Add in the weight of the upper storey's columns, and you easily at the very least match the max floor load.

Love your analogy by the way with the nut on someone's head. But what were the loads that the core columns and core floors were designed for. It's hard to find this information. I don't doubt for a second the buildings came down the way we've been discussing, but I'm just trying to dot the "i's" and cross the "t's".

 

[Pete Tar]

Is the limit to a virtual model computing power, or accuracy of input information? Would this new computer change things significantly?

The result is a system six times more powerful than existing servers that requires eighty times less energy. According to HP, The Machine can manage 160 petabytes of data in a mere 250 nanoseconds.
http://www.iflscience.com/technolog...lating-640tbs-data-one-billionth-second-could

It seems physical models of any size or complexity are just vastly inconvenient in comparison, and though Mick's done well with simplicity I suspect it won't be accepted as a successful modelling of the tower collapse. Funny that he's demonstrated more practical action than the entire AE911 organisation.