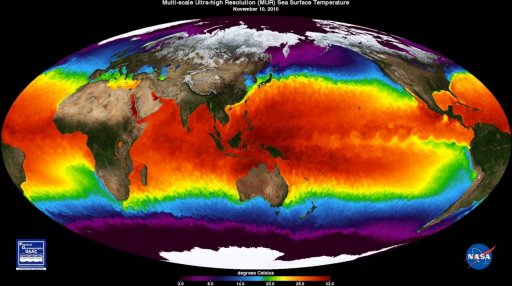
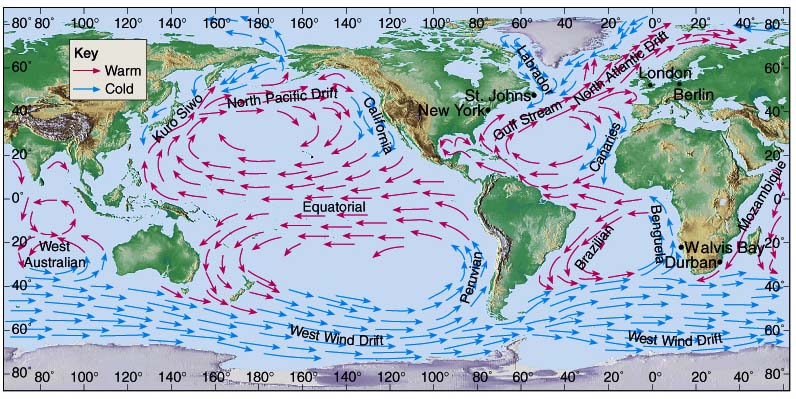
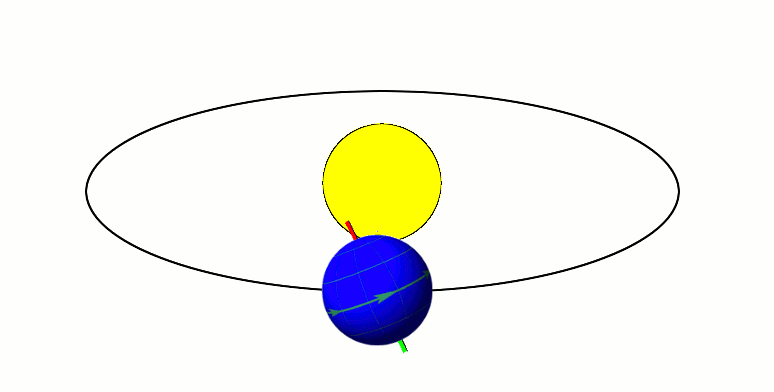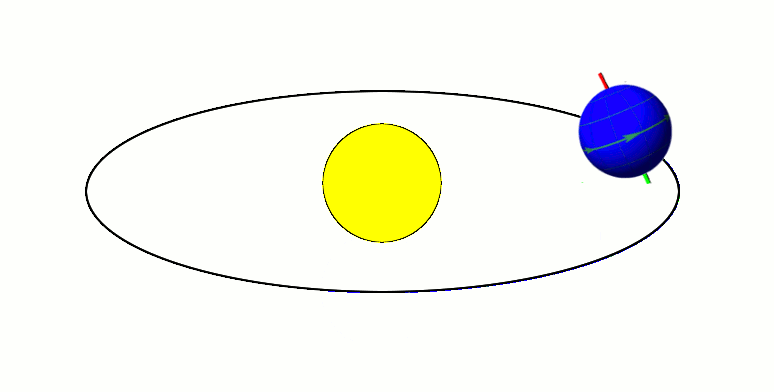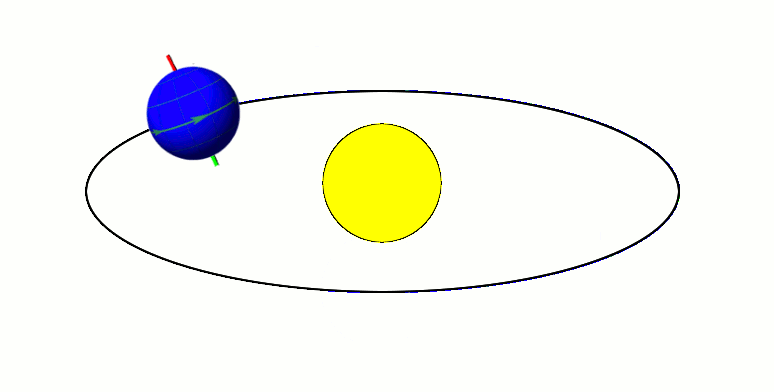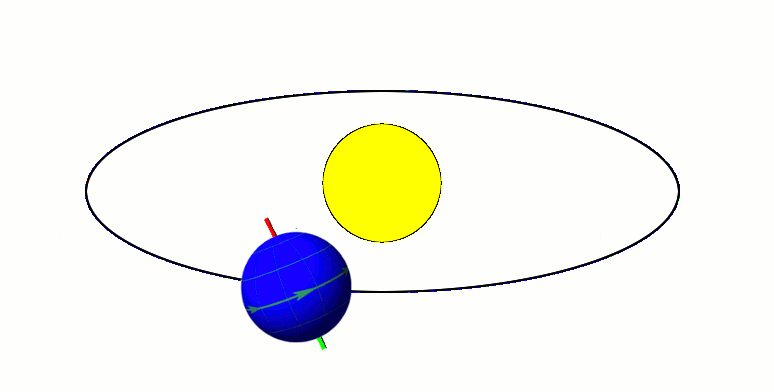
Average annual solar radiation arriving at the top of the Earth's atmosphere is roughly 1361 W/m2.
[34] The Sun's rays are
attenuated as they pass through the
atmosphere, leaving maximum normal surface irradiance at approximately 1000 W/m2 at
sea level on a clear day. When 1361 W/m2is arriving above the atmosphere (when the sun is at the
zenith in a cloudless sky), direct sun is about 1050 W/m2, and global radiation on a horizontal surface at ground level is about 1120 W/m2.
[35] The latter figure includes radiation scattered or remitted by the atmosphere and surroundings. The actual figure varies with the Sun's angle and atmospheric circumstances. Ignoring clouds, the daily average insolation for the Earth is approximately 6 kWh/m2 = 21.6 MJ/m2.
The output of, for example, a
photovoltaic panel, partly depends on the angle of the sun relative to the panel. One Sun is a unit of
power flux, not a standard value for actual insolation. Sometimes this unit is referred to as a Sol, not to be confused with a
sol, meaning
one solar day.
At a lower angle, the light must also travel through more atmosphere. This attenuates it (by absorption and scattering) further reducing insolation at the surface.
Attenuation is governed by the
Beer-Lambert Law, namely that the
transmittance or fraction of insolation reaching the surface decreases exponentially in the
optical depth or
absorbance (the two notions differing only by a constant factor of ln(10) = 2.303) of the path of insolation through the atmosphere. For any given short length of the path, the optical depth is proportional to the number of absorbers and scatterers along that length, typically increasing with decreasing altitude. The optical depth of the whole path is then the integral (sum) of those optical depths along the path.
When the density of absorbers is layered, that is, depends much more on vertical than horizontal position in the atmosphere, to a good approximation the optical depth is inversely proportional to the projection effect, that is, to the cosine of the zenith angle. Since transmittance decreases exponentially with increasing optical depth, as the sun approaches the horizon there comes a point when absorption dominates projection for the rest of the day. With a relatively high level of absorbers this can be a considerable portion of the late afternoon, and likewise of the early morning. Conversely, in the (hypothetical) total absence of absorption, the optical depth remains zero at all altitudes of the sun, that is, transmittance remains 1, and so only the projection effect applies.
[36]