edby
Member
This video
Source: https://youtu.be/0V-tkCzfsT0
from ‘Taboo Conspiracy’ seems to provide apparently solid evidence of flat water. He claims to be filming across from Eagle Park in Saratoga Springs to a place on the other side of the lake where his wife is positioned with a flashlight. The flashlight is clearly visible, and goes off and on when he asks her by phone to turn it off and on.
He does not say where she is located but there is a clear view at 1:04 facing La Quinta Inn and its 3 gables, which places her at about Vineyard Beach on the East side of the lake. She also refers to some ‘steps’, and there are indeed steps down to the beach (about 30 of them, so about 20 feet on the assumption of a US 7” riser). He says the view is over 7 miles, which is consistent with Google Maps.
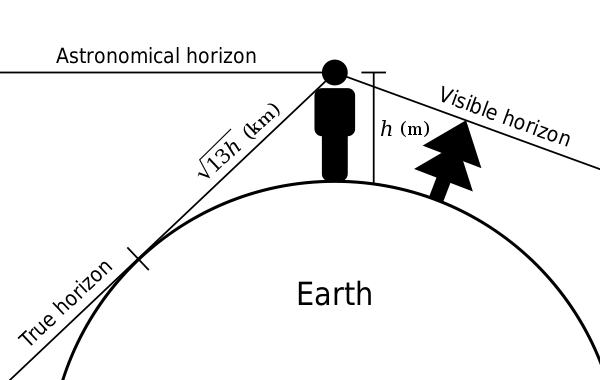
It is hard to fault this. As he points out, about 20 feet should be hidden. My only doubt is whether she is actually at the water’s edge, given that the light first appears when she is at the top of the steps.
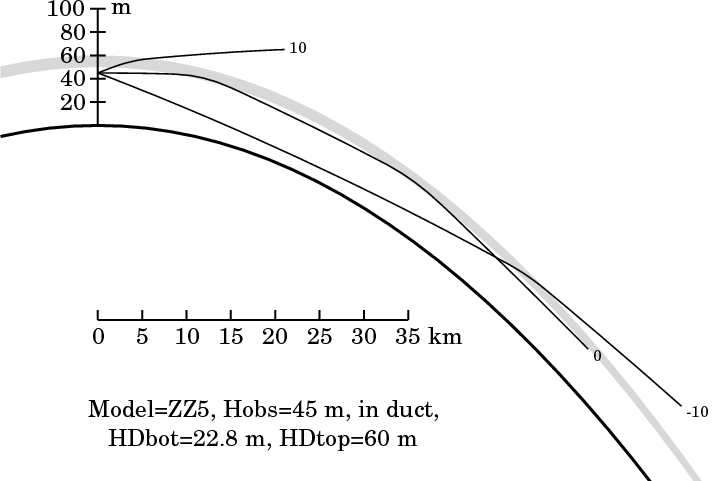
Refraction would not explain why so little was hidden. Any ideas? He claims that anyone can repeat the experiment.
add: coordinates given from another version of the same video locations (says the Youtuber):
Lat: 40.31524628, Lng: -111.76501156
Lat: 40.33612475, Lng: -111.90493711
Source: https://youtu.be/0V-tkCzfsT0
from ‘Taboo Conspiracy’ seems to provide apparently solid evidence of flat water. He claims to be filming across from Eagle Park in Saratoga Springs to a place on the other side of the lake where his wife is positioned with a flashlight. The flashlight is clearly visible, and goes off and on when he asks her by phone to turn it off and on.
He does not say where she is located but there is a clear view at 1:04 facing La Quinta Inn and its 3 gables, which places her at about Vineyard Beach on the East side of the lake. She also refers to some ‘steps’, and there are indeed steps down to the beach (about 30 of them, so about 20 feet on the assumption of a US 7” riser). He says the view is over 7 miles, which is consistent with Google Maps.
It is hard to fault this. As he points out, about 20 feet should be hidden. My only doubt is whether she is actually at the water’s edge, given that the light first appears when she is at the top of the steps.
Refraction would not explain why so little was hidden. Any ideas? He claims that anyone can repeat the experiment.
add: coordinates given from another version of the same video locations (says the Youtuber):
Lat: 40.31524628, Lng: -111.76501156
Lat: 40.33612475, Lng: -111.90493711
Last edited by a moderator: