Explained: Observations of Canigou, Curvature of the Earth & Atmospheric Refraction

[Mick West]

we can decide when the island transforms from a mirage to actual.

Technically a mirage contains an inverted or duplicated image. This is not a mirage, it's a type of refraction phenomenon.

It's a gradual transition, and not one you would be able to pinpoint.

You could actually show this transition to a degree by taking images from those steps. One per step, with Matinicus centered. You'd see what refraction is doing.

 

[eenor]

can you show your perspective math for that?

No, perspective arguments have been made many times elsewhere, look up art tutorials for lessons on 1,2, and 3 point perspective.

 

[Mick West]

the stretching is from the binoculars, I"m kinda surprised you would inset my binoc photo on the non binoc to draw some kind of comparison...

I'm referring to the vertical stretching of the crinkly bits, not the distortion of the image as a whole.

 

[eenor]

Technically a mirage contains an inverted or duplicated image. This is not a mirage, it's a type of refraction phenomenon.

It's a gradual transition, and not one you would be able to pinpoint.

You could actually show this transition to a degree by taking images from those steps. One per step, with Matinicus centered. You'd see what refraction is doing.

Would I? Guess I will have to try this next year. Standby.

 

[Mick West]

No, perspective arguments have been made many times elsewhere, look up art tutorials for lessons on 1,2, and 3 point perspective.

I think you miss the point that the islands are not the same size.

"Why does the 103 foot high Matinicus Isle appear to be significantly lower than the 31 foot high Marblehead Island?"

Rory, you removed the important information there, the distances to the island, (16 miles and 2.5 miles). To get the relative size of something you need to divide by the distance, so we have

Manticus 103/16 = 6.4
Marblehead 31/2.5 = 12.4

So really simply, if we ignore curvature then looking from sea level the high point of Marblehead should be about 2 times the visual height of Manticus. Yet it's actually over 3x

So very roughly we can say that a significant portion of Manticus is hidden behind the horizon.

 

[eenor]

so... you are saying that atmospheric distortion is the cause for the island lowering into the sea in the sea level shots.. but you insist that atmospheric distortion can not raise an image?

Weren't likely in play? what makes you think that? what was the date those photos were taken?

Rory is correct that you are bouncing all over the place, so I might be misunderstanding you.

Bouncing? I'm responding directly to all your questions best I can, to make a thorough observation. Photos were taken last monday and tuesday if I recall correctly. But as said, observed phenom has been lifelong, and doesn't require special atmospheric inversion conditions as required by superior mirage, or looming, which produce a distorted image, not a near perfect reproduction, to my learning. And, yes image distortion at a lower elevation is to be expected over an ocean from the view of a rock for many reasons I've already given.

 

[deirdre]

So very roughly we can say that a significant portion of Manticus is hidden behind the horizon.

plus tree height right?

 

[eenor]

I think you miss the point that the islands are not the same size.



Rory, you removed the important information there, the distances to the island, (16 miles and 2.5 miles). To get the relative size of something you need to divide by the distance, so we have

Manticus 103/16 = 6.4
Marblehead 31/2.5 = 12.4

So really simply, if we ignore curvature then looking from sea level the high point of Marblehead should be about 2 times the visual height of Manticus. Yet it's actually over 3x
View attachment 28681

So very roughly we can say that a significant portion of Manticus is hidden behind the horizon.

emphasis on "roughly" but this is an interesting point, I again, will have to bring a better camera to see detail of Matinicus as I motor towards it, I would again ask when the view transitions from mirage to actual and why the mirage is a picture perfect replica of the actual, to me, a curved atmosphere would distort any raised image, so...is the atmosphere flat?

 

[Mick West]

plus tree height right?

Correct.

 

[Mick West]

in the last bonoc photo
I was standing on grass , near stairs, 10-15 feet above water?

The grass itself there is 16 feet above sea level, so plus 5 to 6 for eye level, plus whatever the tide was.

 

[eenor]

Yes that was my estimate for elevation. So we agree at that elevation, its not a mirage, at grass level we should be looking at roughly half of the actual islands top elevation, or mostly trees. I watched as I moved down, no obvious transformation, but a decrease of viewable area and slight increase (I think because of atmospheric vapor and sea surface movement) of distortion. At rock height at low tide we still should not see anything but estimated 8 ft of tree tops (145 ft below horizon according to curve calculator set (generously) at 1 ft observer height, from 16 miles, island max elev at 103 and estimated max tree height around 50ft). So again, from the rock, I'm looking at what? Not a superior mirage, and seemingly to me more than just 8 ft of tallest possible tree tops at highest point of islands elevation. BTW, the SDSU link has interesting anecdotes at the bottom about other observations that make mine look like mincemeat...any thoughts on that? http://aty.sdsu.edu/explain/atmos_refr/horizon.html

 

[deirdre]

So again, from the rock, I'm looking at what? Not a superior mirage,

you are looking at refraction. an image that has visually moved position due to bending light.

 

[Chew]

View attachment 28678

Can you annotate this pic with an arrow to show where the island in question is?

 

[eenor]

Can you annotate this pic with an arrow to show where the island in question is?

 

[eenor]

you are looking at refraction. an image that has visually moved position due to bending light.
View attachment 28684
View attachment 28685


View attachment 28686

full circle back to refraction....have you been following along?

 

[Mick West]

full circle back to refraction....have you been following along?

You just asked what you were looking at. It is the island, visual lifted up by refraction. If there were no refraction, then you would not be able to see it from the rocks.

 

[Mick West]

View attachment 28687

And closer up, it's the land visible on the horizon.

 

[Rory]

In the last binoc photo I was standing on grass, near stairs, 10-15 feet above water

Thanks for the further info. Please correct me on anything I post below if it's wrong. Just trying to look at the measurements for this pic -

- which you say was taken from the lawn of the house at, I think, 44.067773, -69.068766.

This gives us some actual measurements:

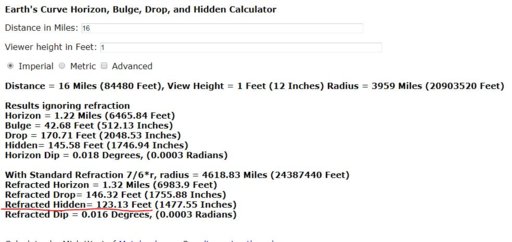
Elevation of lawn above mean sea level: 16 feet
Elevation of camera above lawn: ~5.5 feet
Distance to Marblehead Island: 2.56 miles
Elevation of summit of Marblehead: 33 feet amsl
Distance to Matinicus: ~16.5 miles
High point of NE portion of Matinicus (as seen to left of Marblehead): ~60 feet amsl (not including trees)

I seem to remember you also saying that the photo was taken at low tide, which you said was 9 feet below msl. This gives, with standard refraction:

Predicted amount of Marblehead hidden: None
Predicted amount of Matinicus hidden: 48.3 feet (therefore ~20 feet of high point of NE portion visible, not including trees)

Note: when using the curvature calculator, viewer height is height above water, not height above sea level - so 30.5 feet, in this case.

Though difficult to tell just by eyeballing, it does seem that there's more of Matinicus visible than that predicted by the curvature calculator. Therefore, I suppose we can assume that this photo shows a greater effect of refraction than standard.

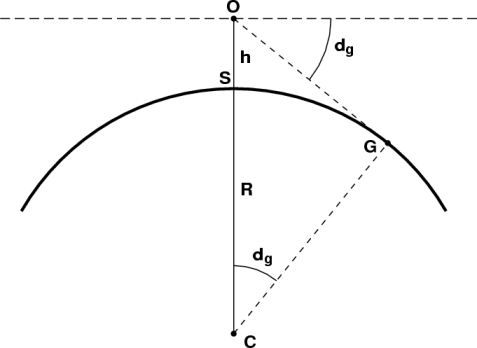
I also looked at what the viewing angles to the various points should be - using the technique outlined here - and compared it to what we see in the photo:

Notes:

• Negative angles are those below "eye level", positive those above
• I used the peak and base of Marblehead as measures in the photos. I don't really find this satisfactory, and would like it if there were more points in the picture
• For both earth models, the apparent height order works out (I was wrong in this earlier)
• For the sphere earth model, the error for the apparent viewing angle to Matinicus is tiny; for the flat earth model, it's significant (16x greater)
• On the sphere earth, all the points are predicted to be below eye level, while for the flat earth model, the two summit points are predicted to be above eye level. Therefore, checking that with a theodolite (next year) could give you more information

Apologies for being late to the show: I wrote most of this much earlier, but got sidetracked with other things, so I guess there's some duplication of information.

Do please check out, though, my using ~69 feet for the high point of NE Matinicus, rather than the island summit elevation of 103 feet (which is to the right of Marblehead).

Also, having horizontally aligned the photo (at the base of Marblehead), I've noticed some significant distortion going on. Thoughts?

Oh, and - since we know the earth's a globe, seeing more of Matinicus must be down to refraction. What else could it be?

 

[Chew]

The tidal datum is referenced to Mean Lower Low Water; heights of rocks, navigation lights, etc are referenced to Mean High Water; but height contour lines and summit elevations are referenced to Mean Sea Level. See the notes and table in the upper left hand corner of chart 13302 for more info. For this area there is a 10 feet difference between MLLW and MHW. This chart unfortunately doesn't provide a correction for MLLW/MHW to MSL.


http://www.charts.noaa.gov/OnLineViewer/13302.shtml


There is a vertical datum database online but it crashes my iPhone.

 

[Trailblazer]

Though difficult to tell just by eyeballing, it does seem that there's more of Matinicus visible than that predicted by the curvature calculator. Therefore, I suppose we can assume that this photo shows a greater effect of refraction than standard.

Perhaps @eenor could repeat the observations on different days and see whether the amount of the island visible varies from day to day. This would be good evidence that refraction plays a role in determining what can be seen: the only other explanation could be the Earth changing size or shape from day to day.

 

[Clouds Givemethewillies]

MSL -half the first column, or the average of the second two, above MLLW?

 

[Rory]

Also, I just documented a visible island in Maine with naked eye and with binoculars placed on a rock at water level during -9 ft low tide [...] I've sailed there many times and watched our house grow steadily smaller on the horizon but not disappear as it should below horizon by 300+ feet.

@eenor - Where did you find the -9ft low tide information?

Also, why do you say your house should disappear by 300+ feet?

 

[Chew]

Where did you find the -9ft low tide information

Tide (and current) data is available online from NOAA. This looks like the closest prediction point: https://tidesandcurrents.noaa.gov/noaatidepredictions.html?id=8415490

 

[Chew]

Oh, hey. Each substation's home page has a link to the various vertical datums. This is for Rockland, the closest substation to the house.

MHW 13.79 Mean High Water

MSL 8.95 Mean Sea Level

MLLW 3.62 Mean Lower-Low Water


Keep in mind though that NOAA chart 13302 (previously linked) uses MLLW as the sounding datum. So the highest point on the island (103' MSL) is 108.3 feet above MLLW.


Source: https://tidesandcurrents.noaa.gov/datums.html?id=8415490

 

[Rory]

Keep in mind though that NOAA chart 13302 (previously linked) uses MLLW as the sounding datum. So the highest point on the island (103' MSL) is 108.3 feet above MLLW.

So when he says it was taken during -9ft low tide, do you think that's inaccurate?

(I know this is all trying to be unnecessarily precise as far as this pic goes - it's more about learning stuff, for me.)

 

[Chew]

So when he says it was taken during -9ft low tide, do you think that's inaccurate?

I'm sure he was referring to how low the water was when compared to high tide.

 

[Clouds Givemethewillies]

MSL -half the first column, or the average of the second two, above MLLW?View attachment 28699

This assumes tides are symmetrical sine waves, which they are not. It depends on the amplitudes and phases of the various harmonics. However it is common to use 'The rule of twelves' to approximate a sine wave, which is good enough for this purpose.
https://en.wikipedia.org/wiki/Rule_of_twelfths

 

[Rory]

To get the relative size of something you need to divide by the distance, so we have:

Manticus 103/16 = 6.4
Marblehead 31/2.5 = 12.4

So really simply, if we ignore curvature then looking from sea level the high point of Marblehead should be about 2 times the visual height of Manticus. Yet it's actually over 3x

So very roughly we can say that a significant portion of Manticus is hidden behind the horizon.

I've got slightly different figures to those above, and so come up with the following:

Matinicus: ~65-69/16.5 = 3.9-4.2
Marblehead: 38.3/2.56 = 15

Meaning Marblehead 'should' be about 3.7x the visual height of Matinicus, going by the above methodology.

Reason our figures are different: I make the highpoint of that part of Matinicus 60-64 feet, and I'm now using the above tide figures of -5.3 feet.

Haven't factored in for tree height on Matinicus; not sure what difference that would make to the figures. Just that: I don't actually know if there are trees at the highpoint, nor, if there are any, how tall they might be.

I'm also wondering if we can ignore curvature in this, and are right in taking it from sea level. Should we not be adding the 'drop' amount?

 

[Mick West]

I'm also wondering if we can ignore curvature in this, and are right in taking it from sea level. Should we not be adding the 'drop' amount?

Adding it to what, and why?

 

[Rory]

Adding it to what, and why?

To the elevation of Matinicus Isle, to get an accurate measure (ie, not ignoring curvature).

But now that I think about it, I don't think that matters: seems the figure required would be the amount of Matinicus that's showing above the horizon (which we don't know, but can guess at).

Also, that viewer elevation isn't important, only distance (ADD, TO CLARIFY: in cases like this, where it's about doing size comparison).

Is that right?

 

[Ph_]

Also, that viewer elevation isn't important, only distance.

As i understood it, it's quite important, see figure.

http://aty.sdsu.edu/explain/atmos_refr/horizon.html

 

[Mick West]

Also, that viewer elevation isn't important, only distance.

It's not important to the size of visible things. It is important to how much of something is hidden by the horizon.

 

[deirdre]

Also, that viewer elevation isn't important, only distance.

well things are shorter the more you look downward on them. but if youre going to dismiss vegetation, I doubt viewer height matters much in comparison.

 

[Rory]

well things are shorter the more you look downward on them. but if youre going to dismiss vegetation, I doubt viewer height matters much in comparison.

Not dismissing, just not currently factoring in, as I don't know how tall the trees are, or if there are any trees at the high point of that part of the island.

 

[Mick West]

well things are shorter the more you look downward on them.

Looking down from a 20 foot elevation change over 20 miles isn't going to produce a measurable difference.

 

[deirdre]

Looking down from a 20 foot elevation change over 20 miles isn't going to produce a measurable difference.

I was going to Marblehead.

 

[Trailblazer]

To the elevation of Matinicus Isle, to get an accurate measure (ie, not ignoring curvature).

But now that I think about it, I don't think that matters: seems the figure required would be the amount of Matinicus that's showing above the horizon (which we don't know, but can guess at).

Also, that viewer elevation isn't important, only distance (ADD, TO CLARIFY: in cases like this, where it's about doing size comparison).

Is that right?

The important thing is to work out the size that the island would be, if you could see all of it. The island doesn't shrink in any way if it is hidden by the horizon, it's just that you can only see the top portion of it.

So if the island should be, say, one quarter the height of a nearby island, and it is actually only one eighth as high, you know that half of it is hidden. (Although of course there may be more than that hidden, and what you are actually seeing is a small portion of the top part "stretched" by refraction.)

 

[Mick West]

I was going to Marblehead.

Even there, 2.5 miles is 13,200 feet. The island would look pretty much identical from 2 feet, 20 feet, and even 200 feet.

 

[Rory]

The important thing is to work out the size that the island would be, if you could see all of it. The island doesn't shrink in any way if it is hidden by the horizon, it's just that you can only see the top portion of it.

So if the island should be, say, one quarter the height of a nearby island, and it is actually only one eighth as high, you know that half of it is hidden. (Although of course there may be more than that hidden, and what you are actually seeing is a small portion of the top part "stretched" by refraction.)

So if the elevation/distance figures say Marblehead would appear 3.7x the size of Matinicus, and the photo shows 3.9x (going by pixel height)...that would suggest we're seeing all of Matinicus?

 

[deirdre]

So if the elevation/distance figures say Marblehead would appear 3.7x the size of Matinicus, and the photo shows 3.9x (going by pixel height)...that would suggest we're seeing all of Matinicus?

did you miss the "stretched by refraction" part? and the trees There was weird weather patterns last week (at least by me) but I think you need to add at least 25-30 feet for the tree line.