Explained: Observations of Canigou, Curvature of the Earth & Atmospheric Refraction

[jeranism]

Mick was just on Joe Rogan and spoke heavily on Flat Earth. One thing he said, was that many flat earth researchers incorrectly report observations of distant points. I agree, many people forget to include the observation height or the height of the observed landmark. However, there are some observations that simply do not make sense on any round earth model and I hope someone can explain to me how these things are seen at such distances.

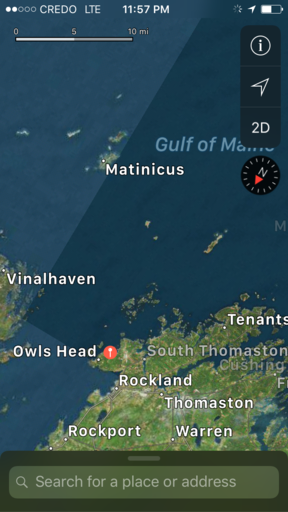
Observation: Twice a year for sure and many other times as well, from Allauch, France you can observe the peaks of several mountains 160 miles away. The known observation is made from a hill in Allauch that is 800 feet above sea level and the highest peak that can be seen is the peak of Canigou which stands 9,137 feet above sea level. Canigou's location makes it visible from the plains of Roussillon and from Conflent in France, as well from Empordà in Spain.

According to Wkipedia:

Twice a year, in early February and at the end of October, with good weather, the Canigou can be seen at sunset from as far as Marseille, 250 km away, by refraction of light. This phenomenon was observed in 1808 by baron Franz Xaver von Zach from the Notre-Dame de la Garde basilica in Marseille. All year long, it can also be seen, with good weather, from Agde, Port-Camargue and the Montagne Noire.
https://en.wikipedia.org/wiki/Canigou

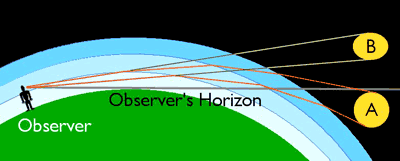
My issue: With the curvature calculator found here: https://dizzib.github.io/ you can see that an observer at 1000 feet looking at an item 163 miles away would find that object 10,631 feet below the horizon. This would place the peak of Canigou well over 1000 feet below the horizon however not only it, but other peaks near it are clearly seen. In the videos below you will see several, sometimes 6 or 7 noticeable and very clear distinct mountain peaks. Even peaks 4000 feet high can be seen and this peak should be over a mile below the horizon.

The Science: I have heard people claim that this is a mirage and or it is refraction. But according to Wikipedia, in optics, refraction is a phenomenon that often occurs when waves travel from a medium with a given refractive index to a medium with another at an oblique angle. This is not actually going on here as we are not changing mediums. This observation (by being a known thing on specific days of the year) and being repeated year after year... tells us it is not a result of a changing refraction issue.

Below please find two videos that show the observation discussed above.

Video 1:


Video 2:


Please explain to me how these peaks are seen on a globe earth.

 

[Trailblazer]

But according to Wikipedia, in optics, refraction is a phenomenon that often occurs when waves travel from a medium with a given refractive index to a medium with another at an oblique angle. This is not actually going on here as we are not changing mediums.

Yes we are. Refraction is caused by a change in optical density. The atmosphere gets denser the closer you get to sea level. That is the cause of atmospheric refraction.

When you take standard refraction into account, from a height of 800ft at 163 miles, only 9,013ft should be hidden. https://www.metabunk.org/curve/

Refraction can be greater or less than the standard amount. I would expect there to be greater variations in temperature, and therefore density, in spring and autumn, which might explain why the mountain is more visible at those times.

In any case, if the Earth was flat, you'd be able to see the whole mountain on any clear day, wouldn't you?

 

[Trailblazer]

There's a page here, in French, explaining what is going on, with diagrams: http://canigou.allauch.free.fr/Explications.htm

Obviously the curve is hugely exaggerated here, but the top diagram shows that only the part of the mountain above about 2,450 metres (8,000ft) is visible.

(Screenshot with automated Google translation)

 

[Rory]

In the OP Jeranism posts both the question and the answer: as he quotes from Wikipedia, "by refraction of light."

Were the observation anything to do with the shape of the earth, the (more or less) same view would be seen on any (clear) day of the year, not just on very select days when conditions were right.

And, as pointed out, a flat earth model predicts that the entire mountain would be visible always, not just the top 10-15%, on a few occasions per year.

This is very similar to images of Corsica from Genoa: known to be due to special conditions of refraction for centuries.

 

[Mick West]

I think the passage from Wikipedia might have been misinterpreted slightly

According to Wkipedia:

Twice a year, in early February and at the end of October, with good weather, the Canigou can be seen at sunset from as far as Marseille, 250 km away, by refraction of light. This phenomenon was observed in 1808 by baron Franz Xaver von Zach from the Notre-Dame de la Garde basilica in Marseille. All year long, it can also be seen, with good weather, from Agde, Port-Camargue and the Montagne Noire.

https://en.wikipedia.org/wiki/Canigou

It might be read as the refraction of light only being good on a few days a year. Really really it's saying that the sunsets are only good a few days a year. Canigou is only visible at that long distance when it's silhouetted agains the setting sun, and the sun sets in different places all year long.

The reference to "good weather" nothing to do with refraction, it just means you need a lack of haze. Standard atmospheric refraction bends the distant horizon image by about the same amount all year long. That's why you can see the sun set slightly after it would be out of view without an atmosphere.

How much is "slightly"?

https://en.wikipedia.org/wiki/Atmospheric_refraction

On the horizon refraction is slightly greater than the apparent diameter of the Sun, so when the bottom of the sun's disc appears to touch the horizon, the sun's true altitude is negative. If the atmosphere suddenly vanished, the sun would too.

So when the sun is touching the horizon, the "real" horizon is just above the top of the sun. About here:

 

[Mick West]

I'm actually very glad this topic came up again, as for some reason I'd remember Canigou as being a distant Island, so I was unable to find it on Google.

Canigou is actually a mountain range on the French mainland, and the viewpoint is from across the bay

This is what the view from Marseille would look like on a Flat Earth

This is what we actually see:

Only the top 1/10th of the mountain is visible. About what we would expect with the curvature of the earth and standard atmospheric refraction.

Here's a closeup showing the fit:

 

[Trailblazer]

It might be read as the refraction of light only being good on a few days a year. Really really it's saying that the sunsets are only good a few days a year. Canigou is only visible at that long distance when it's silhouetted agains the setting sun, and the sun sets in different places all year long.

That makes more sense.

Using Suncalc, you can see that the sunset direction from Allauch (dark red line) points towards Canigou (red dot) on about February 7:

and November 2:

At the current time of year, the sunset direction is nowhere near:

There's a slight discrepancy between "end of October" and the date that seems to align, namely November 2. Probably because the silhouette appears before the sun has completely set, so it is still a few degrees further south than the true sunset.

 

[Trailblazer]

Another example on Flickr, taken on February 9: https://flic.kr/p/bjfebX

With explanation from photographer:

Mount Canigou (alt. 2785m,SW of France, Pyrénées) seen from Allauch near Marseille is distant from 263km. It is the atmospheric refraction of the light which allows to seen this mount. Weather conditions are decisive, clear atmosphere is needed. Twice a year, from the same [place] to observe this phenomena, an alignment with the sun is possible around 9 february and 1 november

 

[Rory]

The very excellent Sly Sparkane has posted a video on this subject, with some very clear and nice graphical representations of the 'missing' 8000 feet of mountain:

 

[eenor]

No, at that distance over the curve the mountain ranges peak should be well below the horizon (1805 feet or almost a half mile!), none of it should be visible, the sun is observed moving across the sky and then behind them....refraction? so the sun plays peekaboo from below the horizon? The french website diagram suggests major mental contortionism. I haven't signed onto flat earth, but cmon, a better explanation is required, and this isn't the only instance of the curve calculator not making sense. Refraction is like some magic word being employed to ridicule a fascinating phenom. You can concentrate on the missing 8000 feet below the horizon, but I'd say thats misdirection. The mountains shouldn't be visible at all in front of the sun setting from that distance, refraction, mirage, gravity, santa claus. Keep trying guys.

 

[Trailblazer]

No, at that distance over the curve the mountain ranges peak should be well below the horizon (1805 feet or almost a half mile!), none of it should be visible, the sun is observed moving across the sky and then behind them....refraction? so the sun plays peekaboo from below the horizon? The french website diagram suggests major mental contortionism. I haven't signed onto flat earth, but cmon, a better explanation is required, and this isn't the only instance of the curve calculator not making sense. Refraction is like some magic word being employed to ridicule a fascinating phenom. You can concentrate on the missing 8000 feet below the horizon, but I'd say thats misdirection. The mountains shouldn't be visible at all in front of the sun setting from that distance, refraction, mirage, gravity, santa claus. Keep trying guys.

Feel free to show us why not, using diagrams. Don't just expect people to take your word for it.

 

[Keith Beachy]

No, at that distance over the curve the mountain ranges peak should be well below the horizon (1805 feet or almost a half mile!), none of it should be visible, the sun is observed moving across the sky and then behind them....refraction? so the sun plays peekaboo from below the horizon? The french website diagram suggests major mental contortionism. I haven't signed onto flat earth, but cmon, a better explanation is required, and this isn't the only instance of the curve calculator not making sense. Refraction is like some magic word being employed to ridicule a fascinating phenom. You can concentrate on the missing 8000 feet below the horizon, but I'd say thats misdirection. The mountains shouldn't be visible at all in front of the sun setting from that distance, refraction, mirage, gravity, santa claus. Keep trying guys.

https://en.wikipedia.org/wiki/Atmospheric_refraction
Refraction is science, it is why, and can't be waved off as magic.
http://aty.sdsu.edu/explain/atmos_refr/horizon.html

 

[Henk001]

No, at that distance over the curve the mountain ranges peak should be well below the horizon (1805 feet or almost a half mile!), none of it should be visible, the sun is observed moving across the sky and then behind them....refraction? so the sun plays peekaboo from below the horizon? The french website diagram suggests major mental contortionism. I haven't signed onto flat earth, but cmon, a better explanation is required, and this isn't the only instance of the curve calculator not making sense. Refraction is like some magic word being employed to ridicule a fascinating phenom. You can concentrate on the missing 8000 feet below the horizon, but I'd say thats misdirection. The mountains shouldn't be visible at all in front of the sun setting from that distance, refraction, mirage, gravity, santa claus. Keep trying guys.

A careful observation of any sunset or moonset will show the atmospheric refraction. In its way towards the horizon the sun or moon flattens and slows down.

 

[eenor]

At what point during the sunset are we viewing a sun being refracted when its actually below the horizon, is that transition observable? If an optical effect, I think we should be able to observe the distortion happening. I understand the false horizon effect which makes the sun distort, become football shaped towards the end of sunset, but that false horizon line is only slightly higher, the line that Mick draws seems drastic. The sun is clearly obscured by the mountains which should be well below the horizon, so if optics are throwing those mountains back above the horizon, then every sunset viewed worldwide would have this effect. Another aspect is that I'm seeing people zoom in on the sun setting "on the ocean" and as they zoom in, it rises above the horizon line again, giving credence to the idea of a vanishing point as opposed to a curve (with current accepted formula). Again, Im not a flat earther, but the Earth curve formula is being tested by all sorts of laser experiments, and that amount of refraction seen from Allauch does not make sense to me, call me silly. If I drew you a diagram, it would simply follow the sun across the sky to the horizon, similar to a drawing illustrating perspective and vanishing point. As far as I've learned, atmospherics play a major role in refraction, yet despite all kinds of conditions, this effect is repeated consistently at this location. Also if a refraction then wouldn't the mountains appear to float above the false horizon or at least show some kind of distortion? Mirage inverts so its obviously not that drastic. The mountains are clearly outlined and the sun is clearly obscured. ok, now bracing for the smug ridicule, but try to make sense, show me other forms of this refraction effect at sunset elsewhere in the world please.

 

[Trailblazer]

The mountains are clearly outlined and the sun is clearly obscured. ok, now bracing for the smug ridicule, but try to make sense, show me other forms of this refraction effect at sunset elsewhere in the world please.

Anywhere where there is a mountain present just "over the horizon" but visible due to refraction, you will see the same effect.

This is the sun setting behind Santa Barbara Island, off the coast of California. Look at how the sun appears flattened. That's due to refraction. It also means that the mountain you are seeing is actually an image moved by refraction, and the mountain (or at least some of the portion you are seeing) is actually below the true horizon.

Also if a refraction then wouldn't the mountains appear to float above the false horizon or at least show some kind of distortion?

Often it does, as in the image at the top of this thread:

See the light appearing to shine "under" the mountain?

 

[AmberRobot]

Another aspect is that I'm seeing people zoom in on the sun setting "on the ocean" and as they zoom in, it rises above the horizon line again, giving credence to the idea of a vanishing point as opposed to a curve (with current accepted formula).

Can you point to a well documented example of this? Vanishing point won't explain a sunset anyway, but I'm curious to see a good example of someone zooming in and seeing movement of the Sun above the horizon.

 

[Mick West]

At what point during the sunset are we viewing a sun being refracted when its actually below the horizon, is that transition observable? If an optical effect, I think we should be able to observe the distortion happening. I understand the false horizon effect which makes the sun distort, become football shaped towards the end of sunset, but that false horizon line is only slightly higher, the line that Mick draws seems drastic.

Which line? The sun at the horizon is visually about 0.5° higher than it actually is (with normal refraction). So basically when it touches the horizon visually it's geometrically below the horizon. The sun's angular size is also about 0.5°

Another aspect is that I'm seeing people zoom in on the sun setting "on the ocean" and as they zoom in, it rises above the horizon line again,

No it does not. It just gets more well defined as the exposure of the camera adjusts to a larger sun in the image, and hence uses a darker exposure, reducing the glare of the sun. If you use a filter you will see the sun stays in the exact same position relative to the horizon through the entire zoom. Unless you see the actual disk of the sun then you are just seeing irrelevant glare.

 

[Trailblazer]

Another aspect is that I'm seeing people zoom in on the sun setting "on the ocean" and as they zoom in, it rises above the horizon line again, giving credence to the idea of a vanishing point as opposed to a curve

This would imply that if you had a strong enough telescope, you could always see the sun, day or night. (Which is what the Flat Earth model implies, anyway). Clearly this isn't true. To the best of my knowledge nobody has ever managed to come up with a telescopic image of the sun when conventional astronomy says it's more than, say 2 solar diameters below the horizon.

 

[Henk001]

then every sunset viewed worldwide would have this effect.

And so it has. This is what happens every sunset:

And this is what you see.

The red circles show a constant movement of the sun about every 3 min. The blue objects show what you actually see. You can check it with a stopwatch or an automatic sequence of photographs every so much minutes.
Al least among (amateur) astronomers it is a well known fact that when you see the sun hitting the horizon it is actually (geometrically speaking) already completely below it. They know the same effect occurs with the setting moon and stars.

 

[eenor]

Still working on the notion of refraction vs vanishing point in regards to the visibility of the Allauch mountains, refraction distorts the disk of the sun as it sets, we all agree, because of the accumulated atmosphere above earth surface between viewer and sun. 2 questions:

1. shouldn't the mountains be also distorted if actually a refraction, at least sightly? Mick was able to overlay the peaks with no distortion in his higher horizon diagram, yet we see the sun distort (and throw light on the water in front of the range making them appear to float which to me further discredits refraction claims).

2. Could what we're seeing be attributed to the idea of a vanishing point (also answering why the mountains are only partially visible)? Of course you'd have to play with the FE notion to consider or allow for this, but ...There are a lot of people making video proofs (as I mentioned earlier) showing plausible small scale (no curve) examples of objects disappearing into the distance on flat surfaces but appearing to disappear over a "curve" when its actually a phenom of vanishing point. Last time I was on metabunk (about the S. Hawkng lake laser test tv show) we came to a standstill on the fact that the limits of our vision coincide with the curve formula. I.E. if a 6 foot person stood 3 miles away from you (say on a "flat" lake bed), it would be equally valid to say that you can't see them because they are below the horizon due to curvature, or that they "disappeared" into the vanishing point. If using a telescope or zoom makes them appear again, are they then a refraction?

 

[Trailblazer]

2. Could what we're seeing be attributed to the idea of a vanishing point (also answering why the mountains are only partially visible)?

Can you explain what you mean by "vanishing point"? The vanishing point is the notional point at which lines of perspective meet. It's not a thing that makes part of an object disappear. Objects keep their shape, they just get smaller and smaller the closer they get to the vanishing point. At the vanishing point, the whole object has shrunk to the point of invisibility.

Put another way, if an object is invisible because it's too small to see, then you can zoom in and it will become visible again. But if it is invisible because there is another object in the way (such as the horizon), you can zoom in as much as you like and it will never reappear. You might as well say that you could make a person standing behind a building reappear by "zooming in".

 

[Mick West]

There are a lot of people making video proofs (as I mentioned earlier) showing plausible small scale (no curve) examples of objects disappearing into the distance on flat surfaces but appearing to disappear over a "curve" when its actually a phenom of vanishing point.

Which particular experiment do you think applies to the situation where 90% (or all) of a mountain (100+ miles away) is below the horizon?

 

[Henk001]

1. shouldn't the mountains be also distorted if actually a refraction, at least sightly? Mick was able to overlay the peaks with no distortion in his higher horizon diagram, yet we see the sun distort (and throw light on the water in front of the range making them appear to float which to me further discredits refraction claims).

Mick's overlay is not precise enough to determine whether the mountain peaks are slightly distorted or not. Any distortion would in this case be in the vertical direction and there is only very little vertical mountain range to distort.

 

[Henk001]

To make clear what a vanishing point is. It has nothing to do with the horizon or eye-level, things I hear sometimes when the "FE notion" on this passes by

The parallel lines seem to converge in a vanishing point somewhere up there. If the stairway would have been much longer you would soon not be able to discern any detail. But things far away don't disappear behind the steps of the stairway. If you zoom in

Essentially nothing "reappears". It was all there but much smaller.
But with things really disappearing behind the horizon, like these windmills

You can zoom in as much as you like

but they won't magically rise above the horizon.

 

[Mick West]

Mick's overlay is not precise enough to determine whether the mountain peaks are slightly distorted or not. Any distortion would in this case be in the vertical direction and there is only very little vertical mountain range to distort.

Here's a close up of the image fit of the Google Earth image and the photo:

The minor discrepancies are probably due to the resolution of Google's elevation model.

As you say, distortion would be vertical (generally compression near the horizon).

 

[Rory]

There are a lot of people making video proofs showing plausible small scale (no curve) examples of objects disappearing into the distance on flat surfaces.

I've seen several of these and they were all due to other factors, such as the camera being slightly below the surface, or angled upwards. What's the best one you've seen?

 

[eenor]

I've seen several of these and they were all due to other factors, such as the camera being slightly below the surface, or angled upwards. What's the best one you've seen?

THere's many, I'm still wading through it with little free time....
https://www.youtube.com/results?search_query=perspective+vanishing+point+horizon+line+flat+earth

Thanks for the overlay detail Mick, yes there seems to be some distortion there, but nothing like the "football" shape of the sun, tho it makes sense that its because the sun is so much farther away that we get more distortion on it.

 

[Rory]

There's many, I'm still wading through it with little free time....
https://www.youtube.com/results?search_query=perspective+vanishing+point+horizon+line+flat+earth

Cool. Do please share it if you come across one that seems like a good one.

 

[Crackton]

I think a lot of conspiracy people have a tendency to take words very literal.

"vanishing point" is used to imply that stuff vanish and can reappear, when it's actually more of an artistic concept regarding perspective of parallel lines.

Image from Wikipedia. The arch doesn't dissapear. It's just a point in view.

 

[Z.W. Wolf]

Let's make it clear that graphical perspective is a technique developed by artists to make their paintings and drawings look more realistic. The vanishing point is a part of this technique. The vanishing point theorem is a mathematical abstraction.

In graphical perspective, a vanishing point is a point in the image plane where the projections (or drawings) of a set of parallel lines in space intersect.

FE believers have developed a belief that the vanishing point is an inherent quality of light. The exact nature of this quality is vague and inconsistent - but it boils down to a belief that something happens to light over a distance. It dissolves or collapses in on itself... or something. The upshot is that light can only travel so far.

They seem to think, or feel really, that optics (telescopes, telephoto lenses, etc.) somehow "uncollapse" the light and make it visible again. Bringing boats back into view from beyond the horizon is one example. This is a mighty feat that can only go so far.

This is why you see comment after comment scorning the idea that the sun and stars could actually be visible over astronomical distances. It wouldn't be possible to put the light back together again.

You'll also see comments about how it would be impossible for a telescope to see something relatively close and something immensely distant such as the moon and a star at the same time. To them it's not a matter of focus. It's a matter of the optics making incoherent light coherent again. To them it's a mighty optical feat to put the light of a star back together again while the light from the moon would be less incoherent and that would be less of an optical feat. How could a telescope do both at the same time?

You'll see comments about how seeing a star at astronomical distances would be impossible for a little camera. The little camera wouldn't have the "power" to put such collapsed or tired light back together. But they don't believe any telescope no matter how powerful could do it. The light of a star at such distances would be too far beyond the "vanishing point of light."

 

[Mick West]

The vanishing point theorem is a mathematical abstraction.

I wouldn't put it quite like that, I mean a "line" is a mathematical abstraction, but you don't want to confuse people by telling them there are no lines. If you have a bunch of parallel lines and you take a photo in between them, then they will converge at an actual point in the photo.

"In the photo" in an important qualifier, because there's nothing in nature.

Of course the photo looks like what you see. But that's because your eye is like a soft camera, so the "vanishing point" is an actual point (scene and eye position dependent) on the image projected on the back of your eyeball.

Difficult to convey to people with no familiarity with the concepts though.

 

[KUDr]

What happens when we look at 3D scene with eyes or camera is called 3D to 2D projection. 3D scene is projected to 2D retina or CCD chip. The perspective in that context is a part of projective geometry that perfectly describes what we see. Parallel perspective lines are lines that never meet. Therefore we say that they meet at infinity (infinite distance from observer).

Vanishing point is just image of that infinity in 2D projection. In 3D scene this point doesn't exist, because it would have to be at infinite distance, so it is never a part of the actual scene. As a consequence no object (even sun or star) can go beyond it.

So all FE videos claiming that the ship, mountain or sun disappears from bottom after it passes the vanishing point are simply wrong. They sometimes show the scene from side where perspective lines cross and the sun is beyond that point. I don't know if it is just misunderstanding or deliberate manipulation with viewer's minds, but it has already affected all FE believers so much that they are not able to understand how wrong they are.

 

[eenor]

View attachment 28635

Can you explain what you mean by "vanishing point"? The vanishing point is the notional point at which lines of perspective meet. It's not a thing that makes part of an object disappear. Objects keep their shape, they just get smaller and smaller the closer they get to the vanishing point. At the vanishing point, the whole object has shrunk to the point of invisibility.

Put another way, if an object is invisible because it's too small to see, then you can zoom in and it will become visible again. But if it is invisible because there is another object in the way (such as the horizon), you can zoom in as much as you like and it will never reappear. You might as well say that you could make a person standing behind a building reappear by "zooming in".

You answered yourself, our vision is limited, if extended (with zoom) and object reappears then vanishing point disappeared it from view, if zoomed in upon and is gone still, curve beyond horizon disappeared object. Lotsa zoomers out there reappearing distant objects...was my initial share.

Also, i just documented a visible island in Maine with naked eye and with binoculars placed on a rock at water level during -9 ft low tide. Easily seen Matinicus Island has 100ft elevation plus trees, its elevation and trees are almost fully visible from Crescent Beach ...23 miles away. Refraction right? Im not convinced, ive sailed there many times and watched our house (my vantage in these pics) grow steadily smaller on the horizon but not distort or disappear as it should below horizon by 300+ feet.

 

[Mick West]

Also, i just documented a visible island in Maine with naked eye and with binoculars placed on a rock at water level during -9 ft low tide. Easily seen Matinicus Island has 100ft elevation plus trees, its elevation and trees are almost fully visible from Crescent Beach ...23 miles away.

In your image above you indicate Fisherman Island, which is 2.3 miles away, not 23.

 

[eenor]

Average atmospheric refraction is 8% , even when doubling that amount, not even the tree tops of Matinicus should be visable from 23 miles away, to my understanding.

 

[eenor]

No, i checked thoroughly, I'm well familiar with Fisherman's, Marblehead and Crescent island, the three in foreground staggered diagonally,

 

[Mick West]

Easily seen Matinicus Island has 100ft elevation plus trees, its elevation and trees are almost fully visible from Crescent Beach ...23 miles away.

Well from your indicated position near Owls Head, it's just 16 miles to Manicus.

 

[eenor]

I also took compass heading to make sure view direction was correct, yes, i attched wrong pic with "marked location " on it, sorry, that is fisherman's

 

[eenor]

Not according to my phone when i mapped to matinicus from my actual location on Crescent Beach, interestingly, Google maps charts the position at 15 miles and draws a line in the middle of open water far from Matinicus, here's one with a legend for miles on it.

 

[Mick West]

It's 16 miles to the Manticus airstrip.

The problem is that it's close to the horizon. Refraction close to the horizon is a different kettle of fish to standard refraction - can be several times as much, with odd distortions . You really need to find something several hundred feet high to get a good measure of how much is obscured by the curve. That's why Catalina works so well.