TWCobra
Senior Member.
Pilots for 9/11 truth published the following article claiming that it is impossible for a 767 to achieve the claimed speeds of the WTC attacks, based on the data obtained from the investigation into the Egypt Air 767 Flt 990 crash in November 1999.
The article appears here: http://pilotsfor911truth.org/wtc_speed
The NTSB report into the crash can be downloaded here: http://www.ntsb.gov/doclib/reports/2002/aab0201.pdf
The claim from Pilots for 9/11 truth is that the Egypt Air 767 broke up at 22,000 feet whilst descending at Mach 0.99, an EAS (Equivalent Air Speed) significantly less than the EAS postulated for, particularly UA FL175 as it approached the South Tower.
At no point in the NTSB report is it suggested that the aircraft broke up in flight.
Furthermore, the so called analysis of the loads on the aircraft neglects to mention that analysis of the FDR has the aircraft at just below 17000 feet, at 485 knots and crucially, experiencing 2.5 G as the Captain fought to regain control.
Furthermore, the aircrafts dual elevators were at opposite ends of their travel as the Captain pulled the control wheel back, and the First Officer was pushing it forward, introducing a large torsion moment on the tail assembly.
Furthermore, from the FDR the maximum Mach of 0.99 was actually experienced at 29500 feet, not 22,000 feet giving an EAS of 361 knots, 1 knot over VMO.
Here is the FDR data.
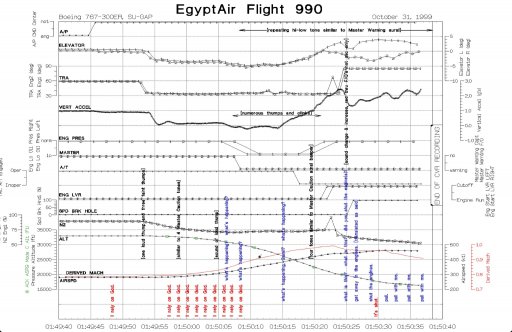
Two facts emerge from this.
1. This 767 airframe underwent a EAS of 462 knots whilst pulling 2.5G and with both elevators at opposite ends of their travel and survived. To say it could survive that and not survive the 1G flight at the speeds of the WTC attacks is not credible.
2. Pilots for 911/truth either did not read the report; couldn't interpret it correctly; or deliberately concocted the breakup/M.99 at 22,000 feet story, to further their own agenda. Take your pick.
For those interested, The NTSB report also contains this paragraph regarding simulations:
The article appears here: http://pilotsfor911truth.org/wtc_speed
The NTSB report into the crash can be downloaded here: http://www.ntsb.gov/doclib/reports/2002/aab0201.pdf
The claim from Pilots for 9/11 truth is that the Egypt Air 767 broke up at 22,000 feet whilst descending at Mach 0.99, an EAS (Equivalent Air Speed) significantly less than the EAS postulated for, particularly UA FL175 as it approached the South Tower.
The NTSB report however does not state that the aircraft broke up at 22,000 feet. As the aircraft was descending both engines were shut down by the Relief First Officer, the person suspected of deliberately crashing the 767 (disputed by the Egyptians but not germane to the discussion), and the aircraft was still intact as it went through 17000 feet when both the FDR and CVR lost power due to the engine shutdown. Radar returns then have the aircraft climbing to 25,000 feet where it began another descent, apparently intact till it crashed into the ocean.
(PilotsFor911Truth.org) - Much controversy has surrounded the speeds reported for the World Trade Center attack aircraft. However, none of the arguments for either side of the debate have been properly based on actual data, until now. Pilots For 9/11 Truth have recently analyzed data provided by the National Transportation Safety Board in terms of a "Radar Data Impact Speed Study" in which the NTSB concludes 510 knots and 430 knots for United 175 (South Tower) and American 11 (North Tower), respectively. A benchmark has been set by the October 1999 crash of Egypt Air 990, a 767 which exceeded it's maximum operating limits causing in-flight structural failure, of which data is available to compare to the WTC Attack Aircraft.
Egypt Air 990 (EA990) is a 767 which was reported to have entered a dive and accelerated to a peak speed of .99 Mach at 22,000 feet. Boeing sets maximum operating speeds for the 767 as 360 Knots and .86 Mach. The reason for two airspeed limitations is due to air density at lower vs. higher altitudes. To understand equivalent dynamic pressures on an airframe of low vs. high altitude, there is an airspeed appropriately titled "Equivalent Airspeed" or EAS[1]. EAS is defined as the airspeed at sea level which produces the same dynamic pressure acting on the airframe as the true airspeed at high altitudes.[2]
Pilots For 9/11 Truth have calculated the Equivalent Airspeed for EA990 peak speed of .99 Mach at 22,000 feet as the equivalent dynamic effects of 425 knots at or near sea level. This airspeed is 65 knots over max operating for a 767, 85 knots less than the alleged United 175, and 5 knots less than the alleged American 11. Although it may be probable for the alleged American 11 to achieve such speed as 430 knots is only 5 knots over that of EA990 peak speed, It is impossible for the alleged United 175 to achieve the speeds reported by the NTSB using EA990 as a benchmark.
Pilots For 9/11 Truth have further studied if a 767 could continue controlled flight at such reported speeds. According to the NTSB, EA990 wreckage was found in two distinct debris fields, indicating in-flight structural failure which has been determined to have occurred a few seconds after recording peak speed. Based on EA990, it is impossible for the alleged United 175 to have continued controlled flight at more than 85 knots over the speed which failed the structure of EA990.
At no point in the NTSB report is it suggested that the aircraft broke up in flight.
Furthermore, the so called analysis of the loads on the aircraft neglects to mention that analysis of the FDR has the aircraft at just below 17000 feet, at 485 knots and crucially, experiencing 2.5 G as the Captain fought to regain control.
Furthermore, the aircrafts dual elevators were at opposite ends of their travel as the Captain pulled the control wheel back, and the First Officer was pushing it forward, introducing a large torsion moment on the tail assembly.
Furthermore, from the FDR the maximum Mach of 0.99 was actually experienced at 29500 feet, not 22,000 feet giving an EAS of 361 knots, 1 knot over VMO.
Here is the FDR data.

Two facts emerge from this.
1. This 767 airframe underwent a EAS of 462 knots whilst pulling 2.5G and with both elevators at opposite ends of their travel and survived. To say it could survive that and not survive the 1G flight at the speeds of the WTC attacks is not credible.
2. Pilots for 911/truth either did not read the report; couldn't interpret it correctly; or deliberately concocted the breakup/M.99 at 22,000 feet story, to further their own agenda. Take your pick.
For those interested, The NTSB report also contains this paragraph regarding simulations:
The Safety Board also conducted simulations in which pilots from Boeing, EgyptAir, the Federal Aviation Administration (FAA), and the Board evaluated the controllability of the airplane following an initial upset that might have been caused by any of these failure scenarios. During these simulations, the pilots were consistently able to regain control of the airplane and return it to straight and level flight using normal piloting techniques, and the airplane could be trimmed to hands-off level flight. In fact, the 767ís redundant actuation system is designed to allow pilots to overcome dual failures such as these.
Even though increased control forces were necessary, recovery could be accomplished by a single pilot using either the left or right control column.102 Further, the simulations also demonstrated that the airplane could climb to about 25,000 feet msl with the engines shut down, even with the speedbrakes extended. The simulation also documented that the engines could have been promptly restarted and (assuming there were no opposing pilot inputs) that the airplane could have been recovered during the climb after the recorders stopped recording. Although the Safety Board recognizes that the simulator did not duplicate the accident airplaneís actual flight conditions in every way,103 such limitations are not uncommon in simulations, and the Board takes those limitations into account when evaluating simulator results. In this case, the Board determined that the differences were not significant and did not affect the validity of the results of the simulations.
Last edited:
