Given that some people claim the curvature of the Earth is not accounted for in surveying, I thought it would be interesting to document various historical instances of this, and of accounting for refraction.
Curvature comes up in two ways. Firstly it arises when determining latitude and longitude by observation of sun and stars. The Earth here is assumed to be a sphere, and the stars essentially fixed in a "celestial sphere" infinitely far away.
Secondly it comes up in the practice of levelling which is the art of determining how high things are above a nominal level surface, such as the surface of the sea. Interestingly this use of the word "level" is often misinterpreted as meaning "flat", when the books on surveying make quite clear this is not the case.
Update: two additional ways in which curvature comes up in surveying, mentioned by @Jon Leighton
Spherical Excess In general, the internal angles of any large surveyed triangle will sum to more than 180 degrees.
Distance corrections including the chord to arc correction, and its inverse, the arc to chord correction.
A treatise on surveying, containing the theory and practice: , John Gummere, 1853, page 239
https://archive.org/stream/treatiseonsurve00gumm#page/238/mode/2up/

A discussion of refraction adjustments, being 1/6 of the curvature adjustment
https://archive.org/stream/treatiseonsurve00gumm#page/242/mode/2up/

A definition of "levelling"
The Theory and Practice of Surveying, Robert Gibson, 1814
https://archive.org/stream/theoryandpracti00gibsgoog#page/n293/mode/2up

Actually from:
A Treatise of Practical Surveying, Robert Gibson, 1777
1808 version on archive.org:
https://archive.org/stream/atreatisepracti01gibsgoog#page/n283/mode/2up

Unfortunately the plates were improperly scanned. What is being referred to is on the left here:
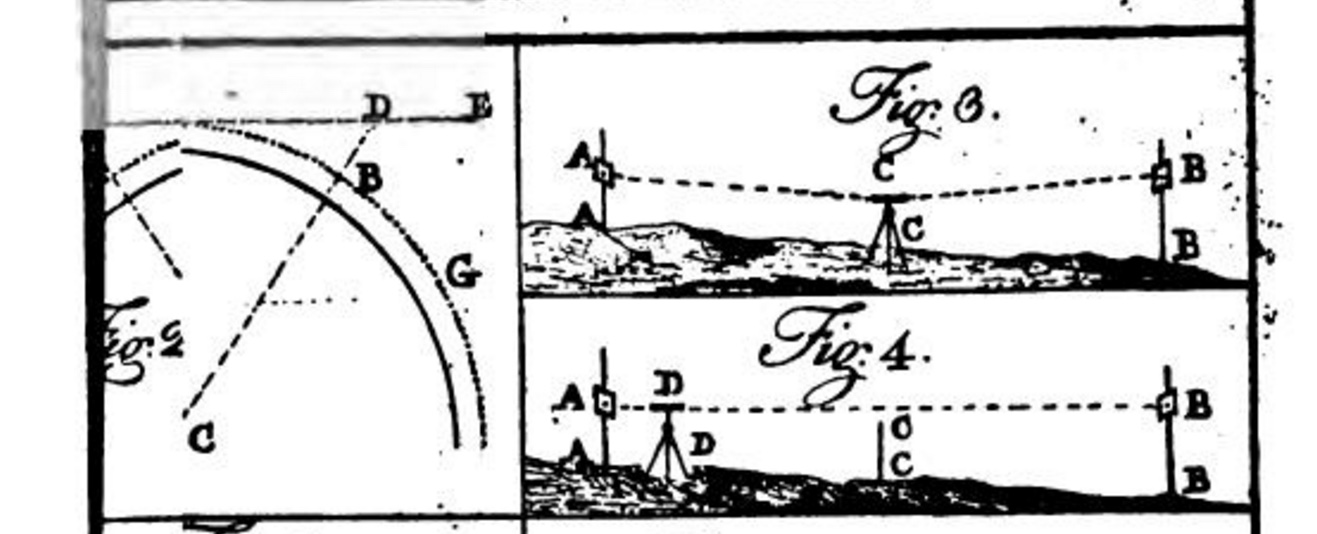
1789 Version does not contain the section on levelling, but does mention the globe and celestial poles
https://archive.org/stream/treatiseofpracti00gibs#page/242/mode/2up/

A similar figure (likely derived from the Gibson work) is found in:
A treatise on surveying and navigation : uniting the theoretical, practical, and educational features of these subjects, by Robinson, Horatio N, 1858
https://archive.org/stream/treatiseonsurvey00robirich#page/n157/mode/2up

(again, note the definition of a level surface)
Slightly off topic, but in this older book, A treatise of practical geometry, published in 1745 (from a 1695 college book written in Latin), we have a discussion on the size of the earth:
https://archive.org/stream/atreatisepracti00greggoog#page/n51/mode/2up

Unfortunately again the figures were not well scanned, and this is all that remains of Fig 22.
Curvature comes up in two ways. Firstly it arises when determining latitude and longitude by observation of sun and stars. The Earth here is assumed to be a sphere, and the stars essentially fixed in a "celestial sphere" infinitely far away.
Secondly it comes up in the practice of levelling which is the art of determining how high things are above a nominal level surface, such as the surface of the sea. Interestingly this use of the word "level" is often misinterpreted as meaning "flat", when the books on surveying make quite clear this is not the case.
Update: two additional ways in which curvature comes up in surveying, mentioned by @Jon Leighton
Spherical Excess In general, the internal angles of any large surveyed triangle will sum to more than 180 degrees.
Distance corrections including the chord to arc correction, and its inverse, the arc to chord correction.
A treatise on surveying, containing the theory and practice: , John Gummere, 1853, page 239
https://archive.org/stream/treatiseonsurve00gumm#page/238/mode/2up/
A discussion of refraction adjustments, being 1/6 of the curvature adjustment
https://archive.org/stream/treatiseonsurve00gumm#page/242/mode/2up/
A definition of "levelling"
The Theory and Practice of Surveying, Robert Gibson, 1814
https://archive.org/stream/theoryandpracti00gibsgoog#page/n293/mode/2up
Actually from:
A Treatise of Practical Surveying, Robert Gibson, 1777
1808 version on archive.org:
https://archive.org/stream/atreatisepracti01gibsgoog#page/n283/mode/2up
Unfortunately the plates were improperly scanned. What is being referred to is on the left here:
1789 Version does not contain the section on levelling, but does mention the globe and celestial poles
https://archive.org/stream/treatiseofpracti00gibs#page/242/mode/2up/
A similar figure (likely derived from the Gibson work) is found in:
A treatise on surveying and navigation : uniting the theoretical, practical, and educational features of these subjects, by Robinson, Horatio N, 1858
https://archive.org/stream/treatiseonsurvey00robirich#page/n157/mode/2up
(again, note the definition of a level surface)
Slightly off topic, but in this older book, A treatise of practical geometry, published in 1745 (from a 1695 college book written in Latin), we have a discussion on the size of the earth:
https://archive.org/stream/atreatisepracti00greggoog#page/n51/mode/2up
Unfortunately again the figures were not well scanned, and this is all that remains of Fig 22.
Last edited:
