FlightMuj
Active Member
Hello all!!!
Eric Dubay posted a video: [Video removed from YouTube]
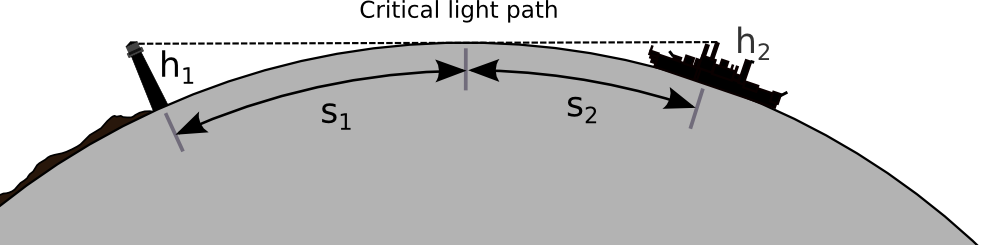
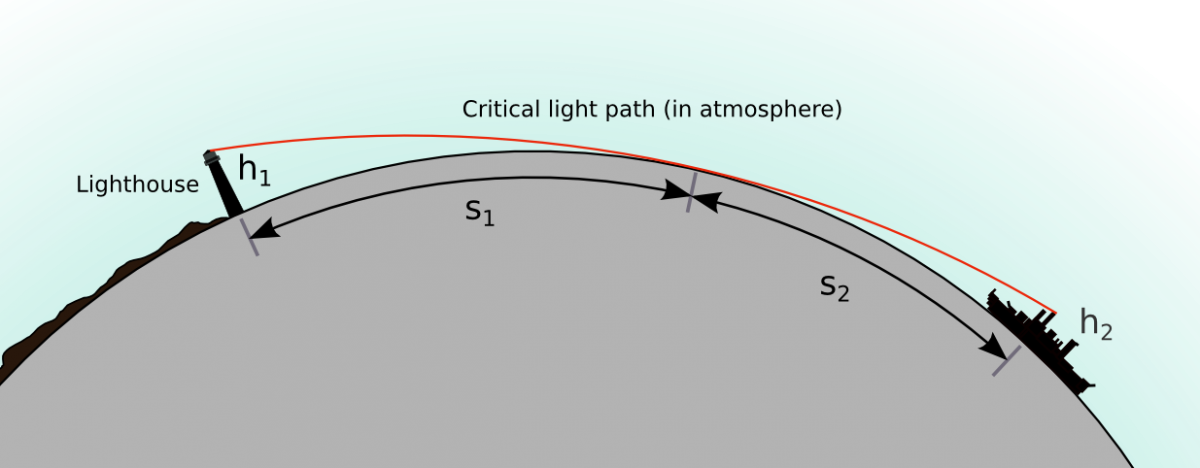
In this video Eric says that the Mountain (or any of them) should not be visible as like Pic Gaspard below.

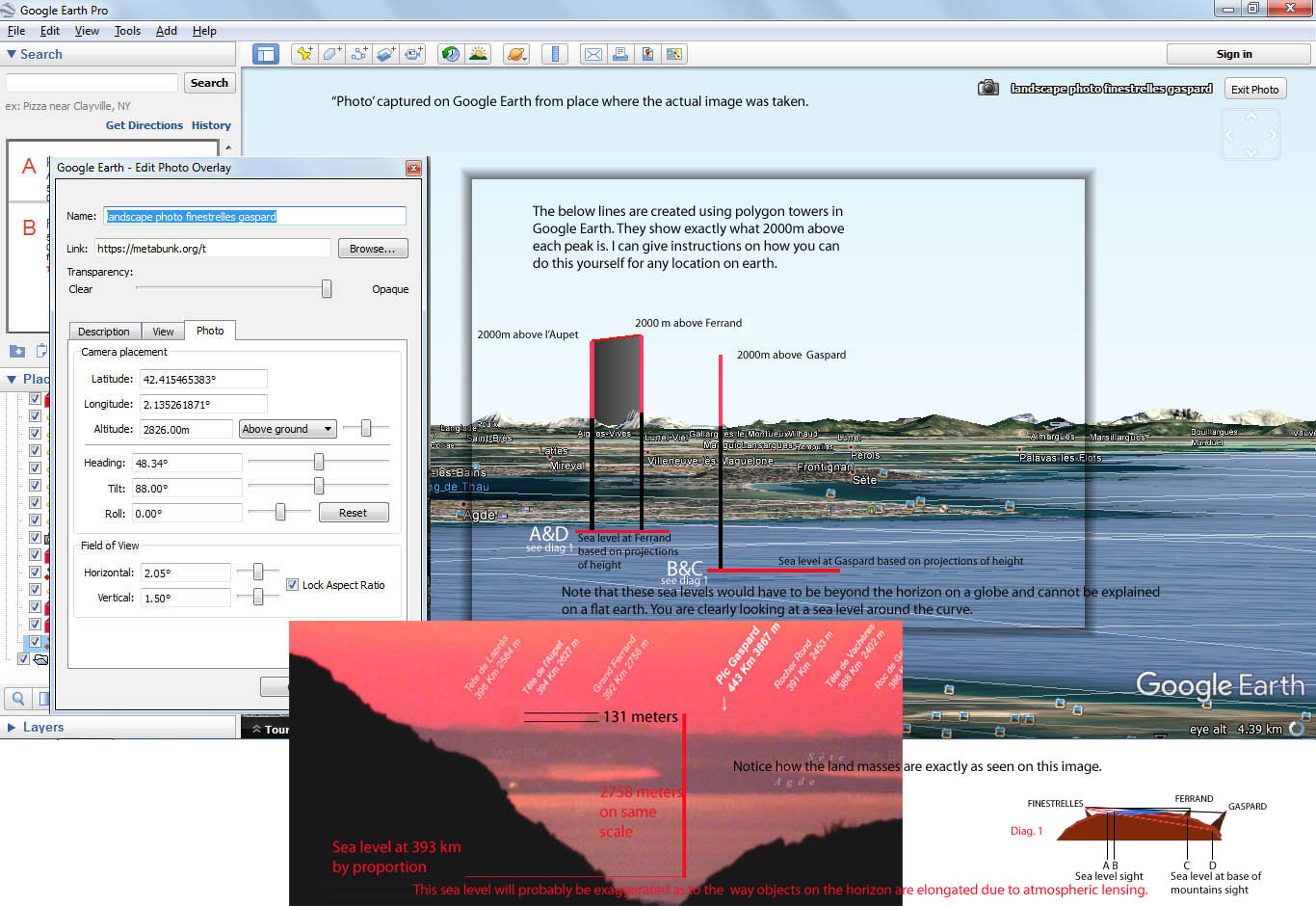
The maximum distance achieved is 443 km, and he does his calculation; evaluates observers height but he misses the point that object's height itself is 3867 m. Nonetheless I tried figuring out myself but could not find a calculator that took into account the target (object) height. There is a link of the photographers work :https://beyondhorizons.eu/2016/08/03/pic-de-finestrelles-pic-gaspard-ecrins-443-km/
I cannot get much information after an hour or two research and this is the first time I am creating a post on a flat Earth debate I otherwise solve and prove it on my own and I am kind of embarrassed that I cannot gather information.
So, simply lack of data has motivated me to write on a forum!!!
P.S. I am a new member and have personally disproved every claim about flat Earth (not bragging; I love it!!!), but I just wanted to research it even if it is a repeated claim . I am not giving my full today so this post is not that detailed, Sorry!!!
Eric Dubay posted a video: [Video removed from YouTube]
In this video Eric says that the Mountain (or any of them) should not be visible as like Pic Gaspard below.

The maximum distance achieved is 443 km, and he does his calculation; evaluates observers height but he misses the point that object's height itself is 3867 m. Nonetheless I tried figuring out myself but could not find a calculator that took into account the target (object) height. There is a link of the photographers work :https://beyondhorizons.eu/2016/08/03/pic-de-finestrelles-pic-gaspard-ecrins-443-km/
I cannot get much information after an hour or two research and this is the first time I am creating a post on a flat Earth debate I otherwise solve and prove it on my own and I am kind of embarrassed that I cannot gather information.
So, simply lack of data has motivated me to write on a forum!!!
P.S. I am a new member and have personally disproved every claim about flat Earth (not bragging; I love it!!!), but I just wanted to research it even if it is a repeated claim . I am not giving my full today so this post is not that detailed, Sorry!!!
Last edited by a moderator: