Rory
Closed Account
A small number of flat earth believers have devised experiments which utilise views of distant mountain ranges. The idea is that distances and elevations can be used to determine whether the earth is flat or a sphere. In some ways, it is something akin to a large scale Bedford Levels experiment, wherein peaks in the far distance can be compared to the apparent heights of peaks in between. It is also known by some as "forcing the line".
The following photograph was taken by a flat earth believer who thought he had discovered an 'impossible' view (as far as the spherical earth is concerned) of the Blue Ridge Mountains in North Carolina.

Source: https://www.youtube.com/watch?v=DPDtMQqlprk
While the conclusion that he came to was shown to be incorrect because of a mistake he made in discerning his elevation and location (thread here) the photo he took is still useful as far as figuring out the shape of the earth.
First of all, the eagle-eyed among you will have noticed that the top of the lookout tower is apparently higher than the summit of Pinnacle Mountain. Whereas, given his viewer observation height of 5481 feet, were the earth flat, he should be looking down at the lookout tower, and up towards Pinnacle.
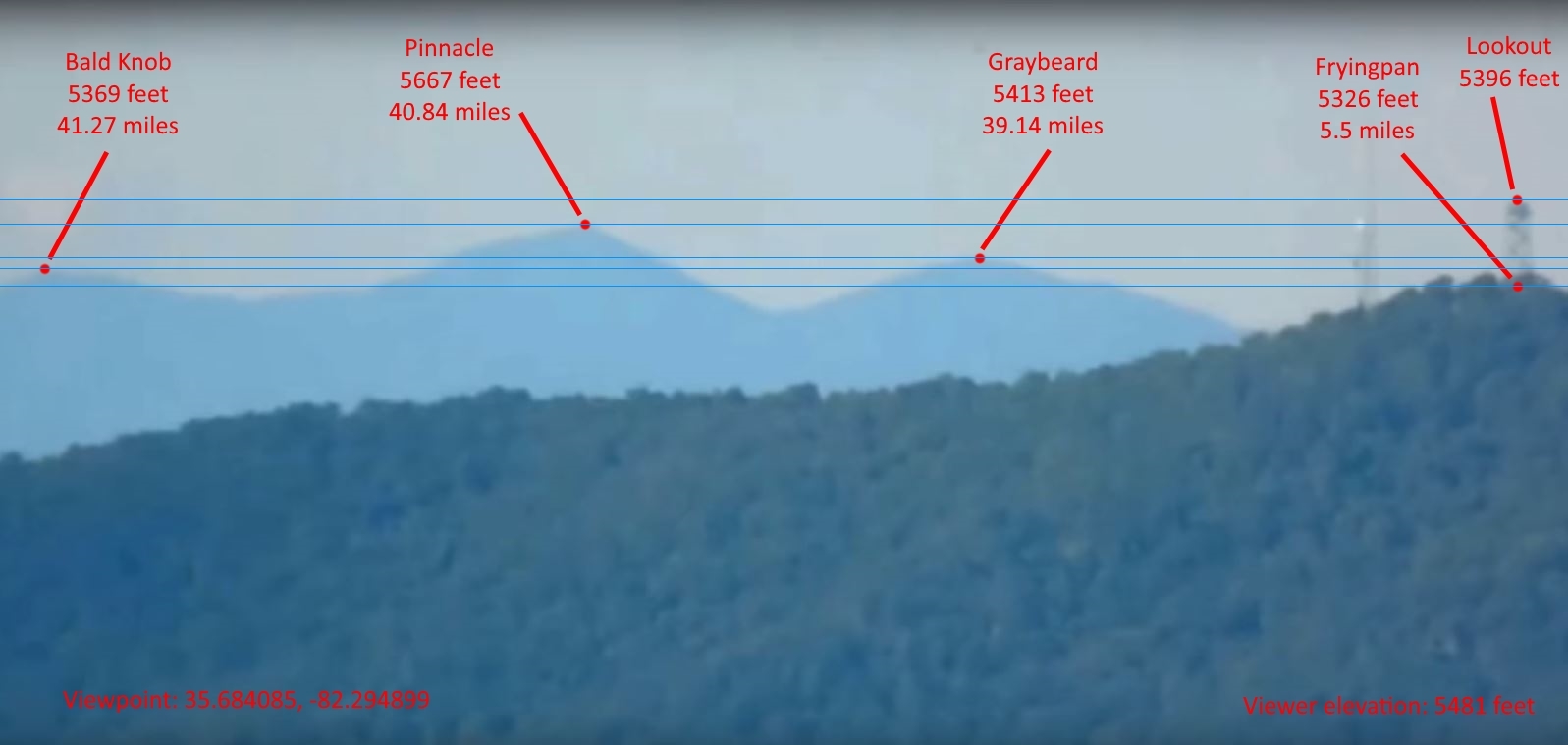
Also, in addition to this, on the flat earth Graybeard would not appear lower than the lookout tower.
So the above photo disproves the flat earth theory that it sought to support - but how does the sphere fare, and how can we test it?
Well, perhaps one of the quickest ways to so do is to work out the angles that are formed between the viewer and the distant peaks. And for that we need the distances, the elevations, and a bit of trig, like so:
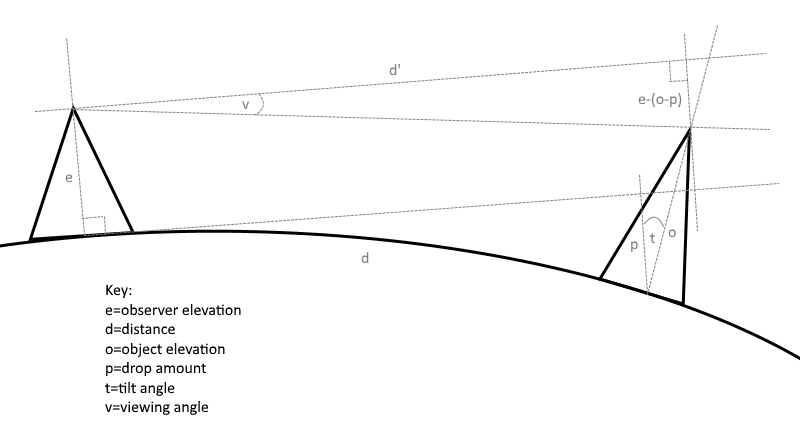
Source: I made this! With MS Paint! ;-)
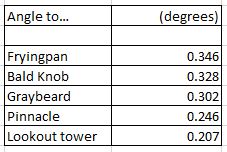
What we would expect to find, were the photograph above to tally with the spherical earth, would be the following:
Whaddya know? It works.
Meanwhile, on the flat earth...
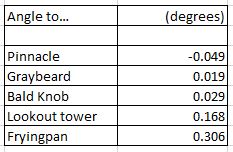
The predicted order of apparent heights is completely out of whack.
Now to Picture #2, which was also used to try and prove the flat earth in a youtube video: this time, a photo of the Colorado Rockies taken from the summit of Snowmass, at 14,105 feet (including six feet for the camera).

Source: http://images.summitpost.org/original/766588.JPG
Again, we can immediately see that this simply doesn't work for the flat earth model. The viewer is looking up to Maroon Peak, but looking markedly down on Mount Shavano, which is higher than both Maroon Peak and the viewer, while Mount Harvard appears lower than Pyramid Peak, even though it's almost 500 feet higher.
Similarly, peaks that should appear to be at about the same apparent height - particularly Castle Peak, and the much more distant Mounts Yale and Shavano - clearly demonstrate a significant difference.
Once again, we see that viewing mountain ranges can be used as a very simple and effective means of testing whether the earth is flat. And, once again, we can use the information in the photo to test the spherical model.
First of all, I'll draw in a different line:

And from that make the following predictions:
Not bad at all: it seems to work. All the viewing angles appear in the corresponding order to the summits in the photo, and at relatively similar intervals to their horizontal positions.
Notes:
The following photograph was taken by a flat earth believer who thought he had discovered an 'impossible' view (as far as the spherical earth is concerned) of the Blue Ridge Mountains in North Carolina.
Source: https://www.youtube.com/watch?v=DPDtMQqlprk
While the conclusion that he came to was shown to be incorrect because of a mistake he made in discerning his elevation and location (thread here) the photo he took is still useful as far as figuring out the shape of the earth.
First of all, the eagle-eyed among you will have noticed that the top of the lookout tower is apparently higher than the summit of Pinnacle Mountain. Whereas, given his viewer observation height of 5481 feet, were the earth flat, he should be looking down at the lookout tower, and up towards Pinnacle.
Also, in addition to this, on the flat earth Graybeard would not appear lower than the lookout tower.
So the above photo disproves the flat earth theory that it sought to support - but how does the sphere fare, and how can we test it?
Well, perhaps one of the quickest ways to so do is to work out the angles that are formed between the viewer and the distant peaks. And for that we need the distances, the elevations, and a bit of trig, like so:
Source: I made this! With MS Paint! ;-)
What we would expect to find, were the photograph above to tally with the spherical earth, would be the following:
- The smallest viewing angle, because it's the highest in the photo, would be to the lookout tower
- Next would come Pinnacle
- Next would come Graybeard and Bald Knob, with fairly similar angles
- The largest viewing angle would be for Fryingpan
- Also, the difference between the angles to Fryingpan and Graybeard, and the difference between the angles to Pinnacle and the lookout tower, judging by the horizontal red lines above, should be roughly similar
Whaddya know? It works.
Meanwhile, on the flat earth...
The predicted order of apparent heights is completely out of whack.
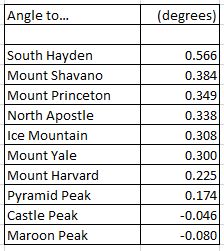
Now to Picture #2, which was also used to try and prove the flat earth in a youtube video: this time, a photo of the Colorado Rockies taken from the summit of Snowmass, at 14,105 feet (including six feet for the camera).
Source: http://images.summitpost.org/original/766588.JPG
Again, we can immediately see that this simply doesn't work for the flat earth model. The viewer is looking up to Maroon Peak, but looking markedly down on Mount Shavano, which is higher than both Maroon Peak and the viewer, while Mount Harvard appears lower than Pyramid Peak, even though it's almost 500 feet higher.
Similarly, peaks that should appear to be at about the same apparent height - particularly Castle Peak, and the much more distant Mounts Yale and Shavano - clearly demonstrate a significant difference.
Once again, we see that viewing mountain ranges can be used as a very simple and effective means of testing whether the earth is flat. And, once again, we can use the information in the photo to test the spherical model.
First of all, I'll draw in a different line:
And from that make the following predictions:
- The mountains on or near the line will have very similar viewing angles
- Maroon Peak and Castle Peak will have the smallest angles
- South Hayden will have by far the largest viewing angle
- Of the peaks on or near the line, Pyramid Peak will have the smallest viewing angle
Not bad at all: it seems to work. All the viewing angles appear in the corresponding order to the summits in the photo, and at relatively similar intervals to their horizontal positions.
Notes:
- This will of course work for all mountain ranges everywhere, as long as we have an accurate elevation for the photographer
- Summit elevations vary from source to source. While this won't affect the conclusion, it will affect the precision of the calculations. (The source I used was the National Geodetic Survey)
- In addition to that, the angles calculated for a globe earth are not perfectly accurate - maybe about 0.01-0.02 degrees off - as I haven't taken into account the difference the 'tilt' would make. It's most likely negligible, but would be nice to have - so if anybody wants to add that to the spreadsheet and return it to me, please go ahead, and I'll update this post
Attachments
Last edited by a moderator:
