Bass In Your Face
Senior Member.
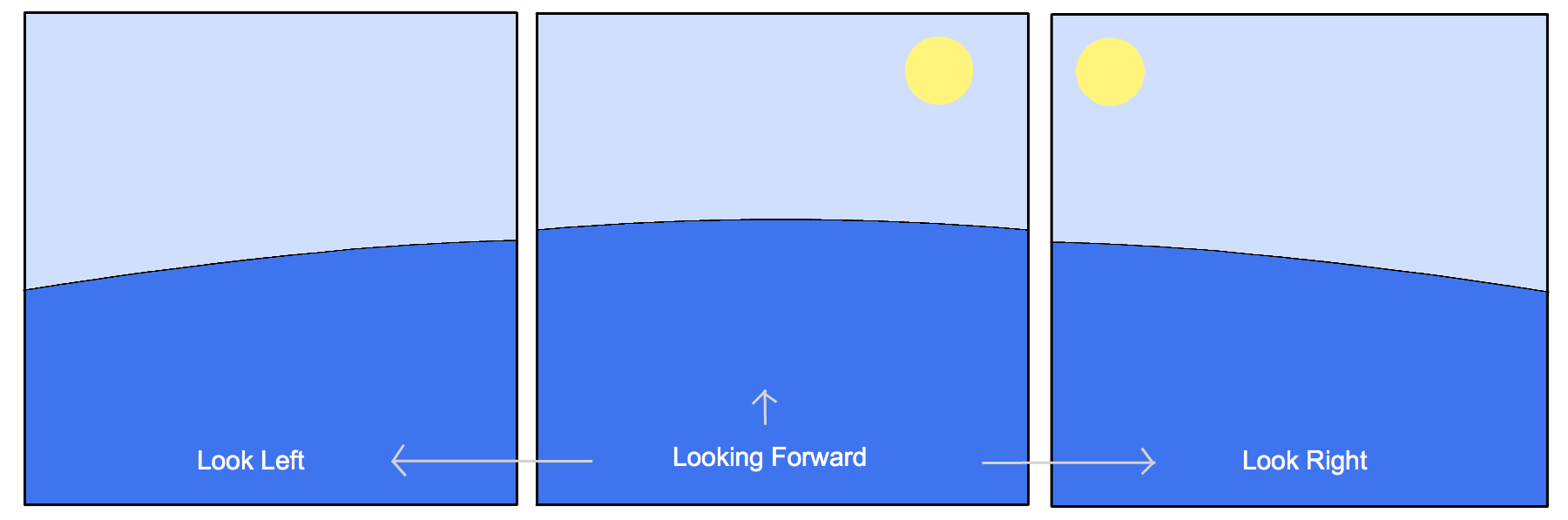
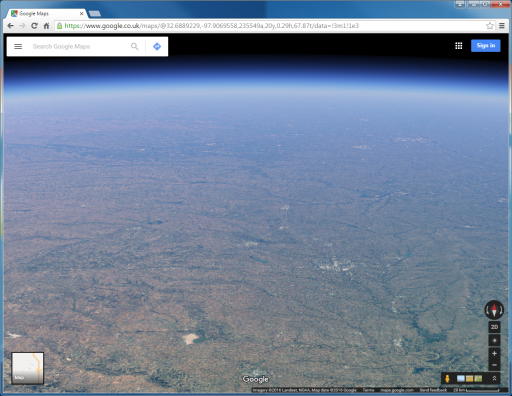
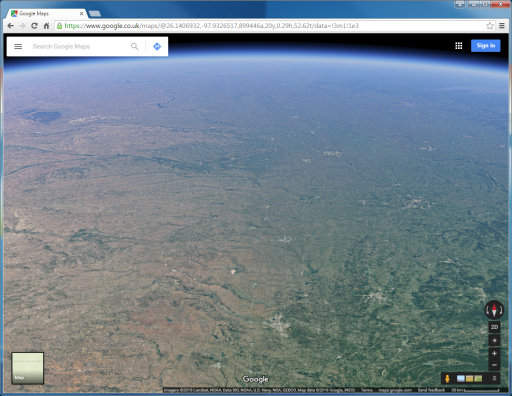
Hey guys, I decided to whip up this experiment at my shop when somebody questioned a graphic of mine that I created to help demonstrate the horizon of a sphere the size of the earth, by zooming in it and showing the FOV. This was the graphic:

(Yes I wrote in the wrong FOV for the last pic :/, should be 35 miles, but it's irrelevant anyways.)
So I received a long response to this claiming I am wrong, and that I am misleading with this comparison.
I completely disagree with him. Here is an example of an argument against "seeing curvature", as well as
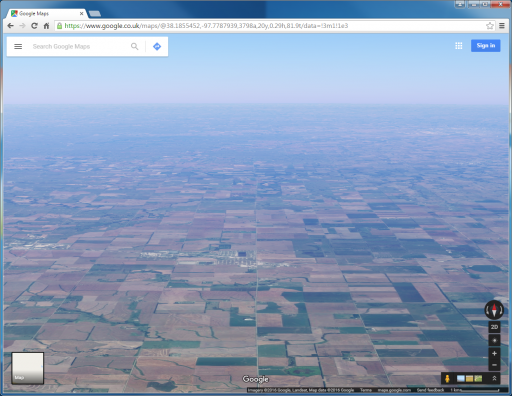
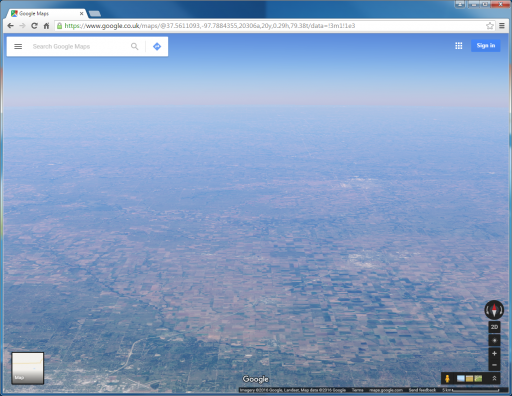
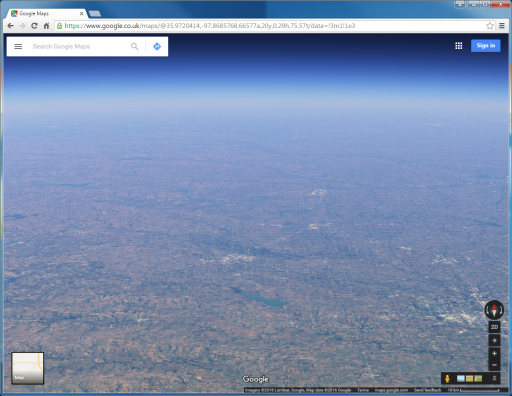
the long response to the graphic above.
and..
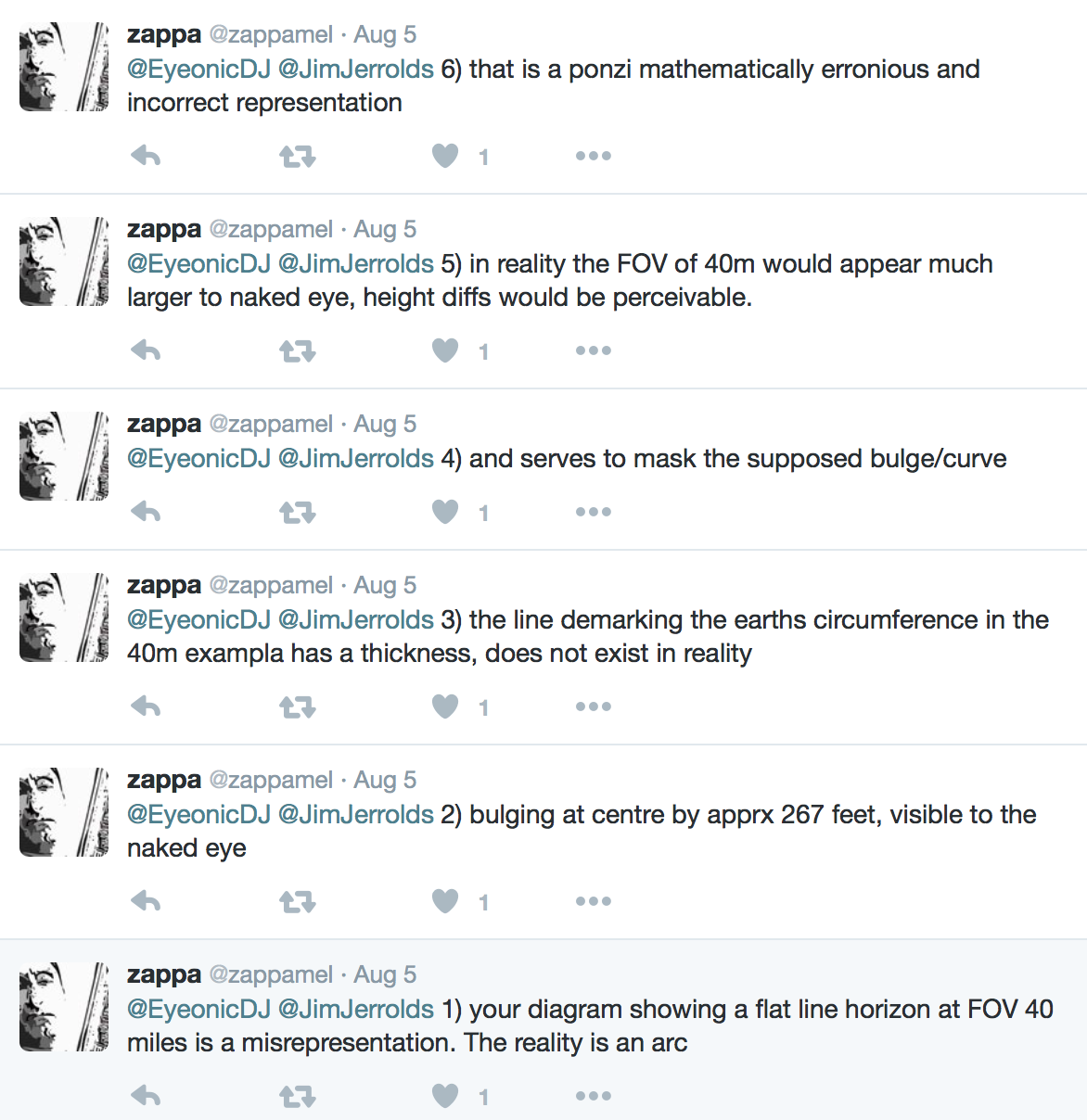
I knew there would come a time when I would need to do this setup without a computer, so this weekend I did. I don't know if it's necessary to post every original photo from my experiment as a whole, so I also made 1 graphic to represent my experiment. My hope is that the result of this can easily be shared on social media as 1 simple graphic instead of having to have long discussions on such simple topics.
I am open to sharing all the photos in their original size, so if that seems important than I will do that. For now, here is my experiment:
(This was created only to demonstrate the relation of the x-axis arc and z-axis arc, mimicking a sphere)

Image is 3163x2034. I took the photos with my Samsung Galaxy S3 (I know I need a new phone) Took me about an hour and a half to set it up and get things measured.
There are a few variables I did not bother to record, as they were not relevant to the purpose of the experiment, so again, the only purpose was to show that the arc on the x-axis, being the same size arc as the z-axis, can look flat, while still seeing curvature in the distance. Its clearly a simple concept, but I have received a few conflicting answers trying to tell me how I am wrong..zoomed in photos of spherical objects, and graphed circles are somehow discounted.
I'd like to reproduce this in the future to possibly answer more than just one question, but I would need more control. I am aware of most things I could do to better this experiment, but for the sake of discussion and open ideas, I'd like to hear any suggestions of how to improve this, or how it could be modified to answer or settle any other questions. (example: camera focus on distant object too blurry, hence my added redline to mark the top of my 1 inch marker)
Thanks guys!

(Yes I wrote in the wrong FOV for the last pic :/, should be 35 miles, but it's irrelevant anyways.)
So I received a long response to this claiming I am wrong, and that I am misleading with this comparison.
I completely disagree with him. Here is an example of an argument against "seeing curvature", as well as
the long response to the graphic above.

and..

I knew there would come a time when I would need to do this setup without a computer, so this weekend I did. I don't know if it's necessary to post every original photo from my experiment as a whole, so I also made 1 graphic to represent my experiment. My hope is that the result of this can easily be shared on social media as 1 simple graphic instead of having to have long discussions on such simple topics.
I am open to sharing all the photos in their original size, so if that seems important than I will do that. For now, here is my experiment:
(This was created only to demonstrate the relation of the x-axis arc and z-axis arc, mimicking a sphere)

Image is 3163x2034. I took the photos with my Samsung Galaxy S3 (I know I need a new phone) Took me about an hour and a half to set it up and get things measured.
There are a few variables I did not bother to record, as they were not relevant to the purpose of the experiment, so again, the only purpose was to show that the arc on the x-axis, being the same size arc as the z-axis, can look flat, while still seeing curvature in the distance. Its clearly a simple concept, but I have received a few conflicting answers trying to tell me how I am wrong..zoomed in photos of spherical objects, and graphed circles are somehow discounted.
I'd like to reproduce this in the future to possibly answer more than just one question, but I would need more control. I am aware of most things I could do to better this experiment, but for the sake of discussion and open ideas, I'd like to hear any suggestions of how to improve this, or how it could be modified to answer or settle any other questions. (example: camera focus on distant object too blurry, hence my added redline to mark the top of my 1 inch marker)
Thanks guys!
Last edited: