How to Take a Photo of the Curve of the Horizon

[Mick West]

(but he excludes the lake Pontchartrain photos)

Very interesting. I've extracted a clip of that here for posterity:

Source: https://www.youtube.com/watch?v=b6KnbI8cTwE


I think also by extension that would mean he would exclude anything that he personally considers "absolutely ridiculous", such as seeing the curve from 500 feet, or JTolan showing the curve. Or anything with a curve.

So here we've got numerous photos of the curve of the horizon from around 500 feet, based on the technique first proposed here by @Clouds Givemethewillies, and now with these excellent examples and advice from @Rory. So what could the response be from the Flat Earth community?

We've seen before a consistent pattern of asking for evidence, being given evidence, and then rejecting that evidence on some spurious grounds. So I'm interested in what they will say to reject this.

 

[xena]

Seriously. That's the curve of the earth ? The earth would be tiny if your saying that's the curve of the earth .
[off topic material removed]

 

[Mick West]

Seriously. That's the curve of the earth ? The earth would be tiny if your saying that's the curve of the earth .
[off topic material removed]

It is the curve of the horizon. When you are at 500 feet then the horizon is a 30-mile radius flat circle that's 1000 feet below you. It's a slight curve, so you have to magnify it to see it (or get really high)

Maybe you could draw a picture of what you would expect to see on a globe from 500 feet?

 

[xena]

Why would I draw a picture? Looking at that photo the amount of curve is ridiculous.
There is no way you would have that much curve in such a short distance . Why do you have to magnify the curve anyway.
That seems to be a real issue with this subject . Everyone seems happy to alter the simple viewing experience to prove their point . I am not a flat earther and I have never seen the curve of the earth whilst as a passenger in a plane or as a pilot in a plane ( I used to fly ) .

 

[Mick West]

Why would I draw a picture? Looking at that photo the amount of curve is ridiculous.

Which photo are you referring to?

The amount of curve here seems very slight, and if you do the math it is the exact amount that you would expect.

 

[Rory]

That's the curve of the earth? The earth would be tiny if you're saying that's the curve of the earth.

That's true: if that was the curve of the Earth the Earth would be tiny - and one thing I've learned when discussing this with people is it's not always obvious what we're seeing here, and that not many people are immediately aware of the difference between the curve of the Earth and the curve of the horizon.

What we're seeing here is the curve of the horizon, which exists as a result of the surface of the Earth being curved.

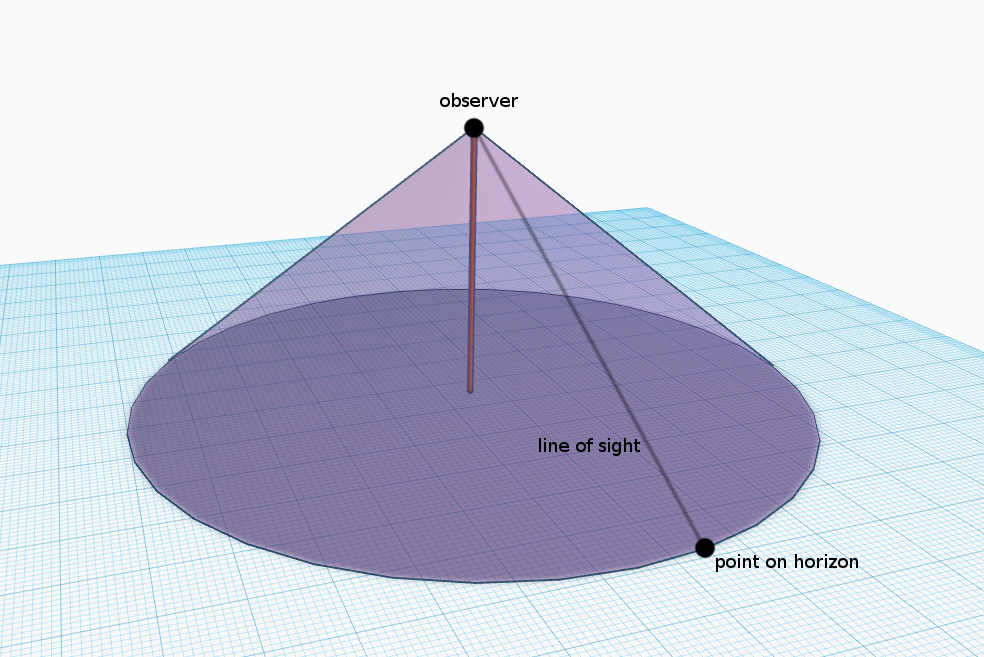
The clearest and easiest way I've found to understand it is to think of the horizon as the edge of a flat disk, with the observer hovering above the centre of it - which is how it would be if one was, say, on an oil rig in the middle of the sea.

Maybe these pictures will help:

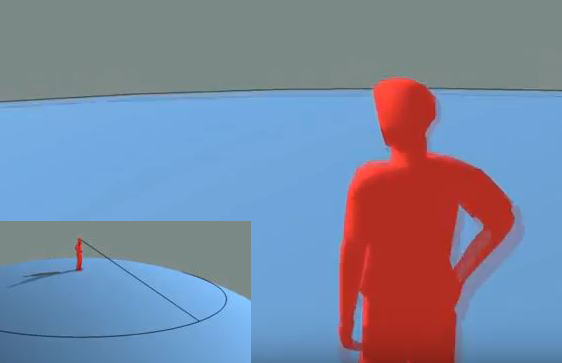
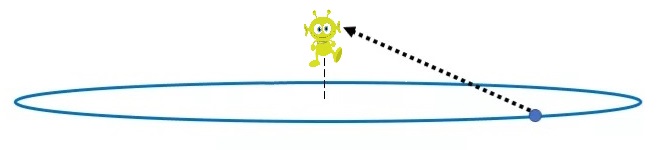
Obviously not to scale, but I think they help illustrate the point. The red guy is on a sphere and whichever direction he looks in, the horizon is always the same distance away, forming a 360° circle, which is what we're seeing in these photos.

The amount of curve actually depends on the observer's elevation, as shown in this diagram here:

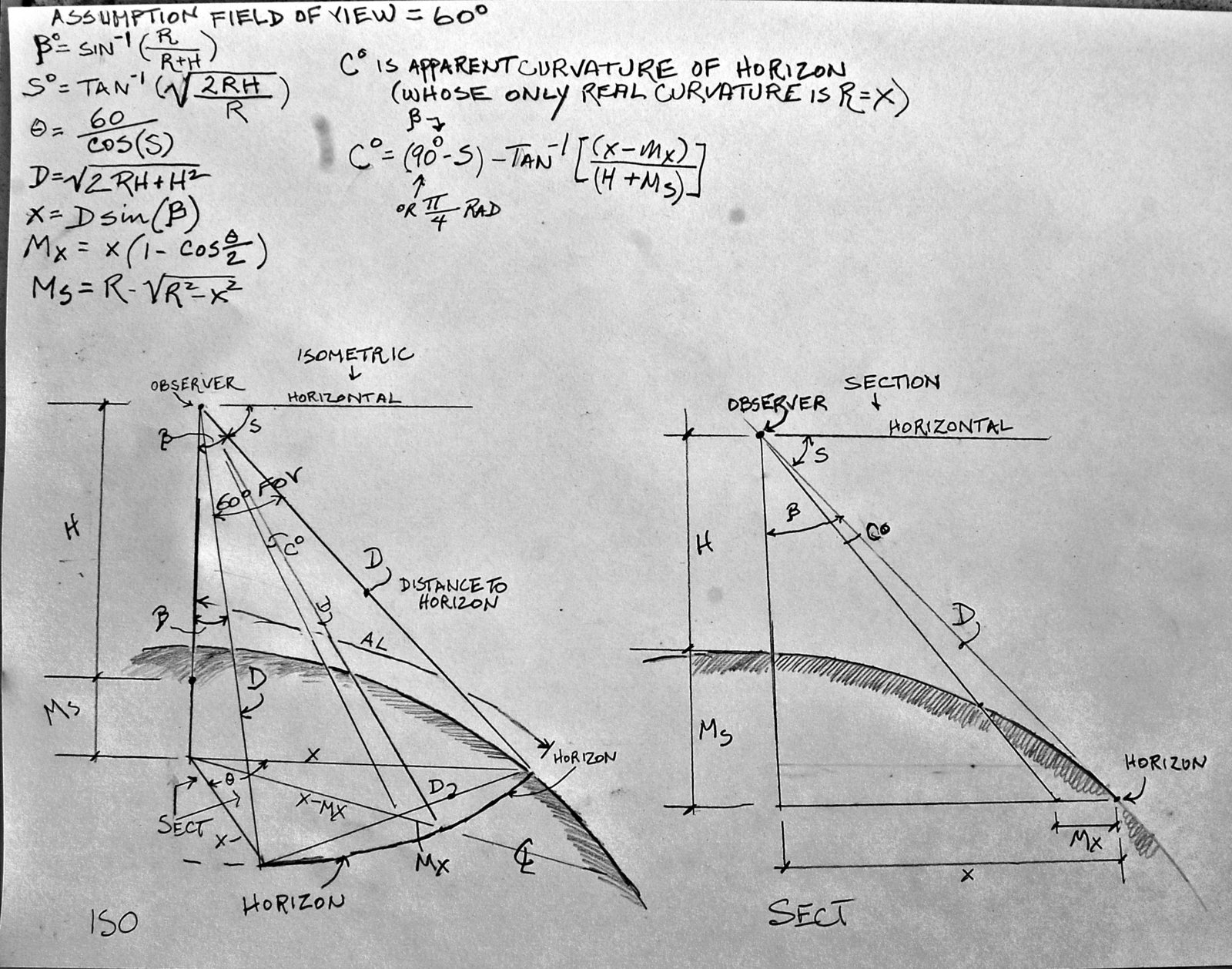
The difference between the curve of the Earth and the curve of the horizon perhaps helps explain Neil deGrasse Tyson's puzzling statement that Felix Baumgartner wouldn't have seen the curve of the Earth from 120,000 feet: we'd actually have to be many thousands of miles away to see the a curve that wasn't the curve of the horizon, and even the astronauts on the ISS are still seeing 'the curve of the horizon' - admittedly a very large and unmistakeable one, at that altitude.

Why do you have to magnify the curve anyway? That seems to be a real issue with this subject.

By "magnify", do you mean "why do we have to vertically stretch the images?"

Actually, we don't. This video from a pilot flying at 46,000 feet very clearly shows the curve of the horizon without any "magnification":


Source: https://www.youtube.com/watch?v=9DDwx18JT9Y

And in this one I zoom in on a photo I took and show that the curve can be seen very clearly without having to vertically stretch:


Source: https://www.youtube.com/watch?v=tOCodgq1oM8&t=35s

Here's a crop of the horizon from that photo, with a straight line drawn underneath it (click to enlarge):

Apart from the crop and the straight line, it's an unmodified image.

I've put all these 'curve of the horizon' images into a public google drive folder, if anybody wants to download them.

 

[xena]

Which photo are you referring to?

The amount of curve here seems very slight, and if you do the math it is the exact amount that you would expect.

The bubble in the spirit level is off centre . Also if the bubble was centered the line to the right would show a bigger gap . But it is straight not curved . Looks very much like the tripod is not on even ground . No curve just not straight .

 

[Mick West]

The bubble in the spirit level is off centre . Also if the bubble was centered the line to the right would show a bigger gap . But it is straight not curved . Looks very much like the tripod is not on even ground . No curve just not straight .

The edge is straight. Compare that edge against the horizon.
Try printing it out, laying it flat and looking along it.

 

[Rory]

The bubble in the spirit level is off centre. Also, if the bubble was centered the line to the right would show a bigger gap. But it is straight, not curved. Looks very much like the tripod is not on even ground. No curve, just not straight.

Maybe it would be useful also to look at the more recent shots, in which the curve is somewhat clearer, such as those in Post #38.

Here's an uncompressed version of one of those:

 

[xena]

Maybe it would be useful also to look at the more recent shots, in which the curve is somewhat clearer, such as those in Post #38.

Here's an uncompressed version of one of those:

Rory thanks for your response . Post #38 shows what would be a impossible amount of curve . If you zoom in using cameras the photos tend to curve . I've taken a photo of my table like that and it curves . Try it for yourself and see what conclusion you come to . The photo above clearly shows no curve and and again why would there be curve at only one direction.

 

[Mick West]

Rory thanks for your response . Post #38 shows what would be a impossible amount of curve . If you zoom in using cameras the photos tend to curve . I've taken a photo of my table like that and it curves . Try it for yourself and see what conclusion you come to . The photo above clearly shows no curve and and again why would there be curve at only one direction.

I think you misunderstand what is being shown. This is the SAME image as in post #38, just compressed horizontally (or stretched vertically, depending on how you think of it) The compressed image is a simple linear compression. Straight lines will remain straight, curved lines will get more curved. We see the straight lines of the red straight edges remain straight, yet the adjacent horizon gets more curved.

If it was not curved, then it would be straight, like the straight edges.
If the camera was distorting it, it would also distort the straight edges.

Hence the ocean horizon is visibly curved in reality.

 

[Mick West]

@zena, here's an animation of what @Rory did. All that happens is the image is stretched vertically. Straight lines remain straight. The horizon is curved.


Source: https://giphy.com/gifs/XbIYp57A0oVB8Zc1lV/html5

 

[Rory]

I've taken a photo of my table like that and it curves. Try it for yourself and see what conclusion you come to.

I've tried it many times: when straight lines are photographed in the centre of the frame, they stay straight, and don't curve.

If your table appeared curved when you zoomed in on it, either it wasn't in the centre of the frame, or it isn't as straight as it appears.

Try taking a photo of a known straight edge and centre it in the frame. Something like the four straight edges in the gif above, which form the window above and below the horizon.

 

[Trailblazer]

we'd actually have to be many thousands of miles away to see the a curve that wasn't the curve of the horizon

To be pedantic, however far away you are you're always seeing the "curve of the horizon", but that gets closer and closer to seeing the perimeter of the whole globe.

From a related thread:

So, from an aircraft at 40,000ft (7.5 miles), the fraction of the Earth visible is:

f = 7.5 (2 x (3959 + 7.5)) = 0.00095, or just under 0.1%

From the International Space Station at 240 miles, it is 2.9%

From the moon at 238,900 miles, it is 49.2%



There is no "dividing line" between seeing the curve of the horizon and seeing the curve of the globe, but psychologically the transition would probably occur when you could start to see both edges of the horizon in your field of view at once, or nearly so. Assuming a field of view of about 120 degrees, that would happen at an altitude of (r/sin60º) - r, or 612 miles.

If you play around with Google Earth, zooming in and out, there's definitely a point at which the perception goes from "I'm looking at the horizon" to "I'm looking at a ball", but it's a gradual thing.

 

[DavidB66]

we'd actually have to be many thousands of miles away to see the a curve that wasn't the curve of the horizon

Not necessarily. In Soundly's images of the Lake Pontchartrain causeway, taken from an angle somewhat to the side, we can see the curve of the causeway, which is not a curve of the horizon but a great circle arc. There are also some photos of a long straight road across the Bonneville Salt Flats, taken from a nearby hillside, which show a noticeable curve. (I can't immediately find an example, but I'm sure I've seen some.) Such examples are rare, because they require a sufficiently long straight level structure to be visible within the observer's horizon, and from a suitable angle. (Viewing them from 90 degrees would probably not work, because the curvature is so slight.) Just looking at a large expanse of sea (or lake) is not sufficient, because there is nothing to distinguish one bit of water from another.

 

[Mick West]

In Soundly's images of the Lake Pontchartrain causeway, taken from an angle somewhat to the side, we can see the curve of the causeway, which is not a curve of the horizon but a great circle arc.

I thought you meant this:

Discussion on that topic here:
https://www.metabunk.org/a-side-view-of-the-curvature-of-the-earth-at-lake-pontchartrain.t9268/
Reading it again there seems to be some unresolved questions there.

But did you actually mean this?

Such examples are rare, because they require a sufficiently long straight level structure to be visible within the observer's horizon, and from a suitable angle. (Viewing them from 90 degrees would probably not work, because the curvature is so slight.)

The first example is a 90° view on the pylons, more or less. But they seem to be mostly beyond the horizon, which is flat as the camera is very low altitude. It's an interesting mix.

 

[DavidB66]

I thought you meant this:

Discussion on that topic here:
https://www.metabunk.org/a-side-view-of-the-curvature-of-the-earth-at-lake-pontchartrain.t9268/
Reading it again there seems to be some unresolved questions there.

But did you actually mean this?
View attachment 37013




The first example is a 90° view on the pylons, more or less. But they seem to be mostly beyond the horizon, which is flat as the camera is very low altitude. It's an interesting mix.

I was thinking of your second example, and other similar shots by Soundly. If I recall correctly, the first example is created by stitching together frames from a long panning sequence. It does not show what could be seen by an observer in any single view. Moreover, as you point out, the pylons at each end of the sequence are partly below the horizon. They reveal the curvature of the earth in the same way as ships going 'over' the horizon. Which is still useful, but not the same as seeing the curve in a single view. I should probably have said in my earlier comment that it is necessary to have quite a high viewpoint (as well as the other conditions I mentioned) in order to get a sufficient area within the horizon. In Soundly's causeway example the shots were taken from a high building overlooking the lake, while in the Lake Bonneville example (I wish I could find it!) the view is from a high hill. But with the availability of drones this requirement is becoming less of a constraint.

 

[xena]

I think you misunderstand what is being shown. This is the SAME image as in post #38, just compressed horizontally (or stretched vertically, depending on how you think of it) The compressed image is a simple linear compression. Straight lines will remain straight, curved lines will get more curved. We see the straight lines of the red straight edges remain straight, yet the adjacent horizon gets more curved.

If it was not curved, then it would be straight, like the straight edges.
If the camera was distorting it, it would also distort the straight edges.

Hence the ocean horizon is visibly curved in reality.

I understand that it is compressed . If you took the same photo upside down it would curve the opposite way .
Straight lines do not remain straight if you use a go pro for example .

 

[deirdre]

I understand that it is compressed . If you took the same photo upside down it would curve the opposite way .
Straight lines do not remain straight if you use a go pro for example .

you are still missing the point. If the horizon was flat/straight like the red bars, then the redbars would curve the same way as the horizon in this photo when you compress them.

Because the red bars and the horizon behave differently under compression, it proves that the horizon is different than the red bars. ie. the horizon is not flat/straight.

 

[xena]

you are still missing the point. If the horizon was flat/straight like the red bars, then the redbars would curve the same way as the horizon in this photo when you compress them.

Because the red bars and the horizon behave differently under compression, it proves that the horizon is different than the red bars. ie. the horizon is not flat/straight.
View attachment 37014

Understand that , but if you look ,some of the sea is straight and not curved the sort of bulge is in the middle and less to the outer ,it not even a "even " curve. The objects in front are also much closer and smaller so you would not see them curve. The curve of the sea is not even . IMO it should be .

 

[deirdre]

the sort of bulge is in the middle and less to the outer

that's how balls work.

it not even a "even " curve.

yea its a bit lopsided. But his red bars are lopsided too.

The objects in front are also much closer and smaller so you would not see them curve.

no. its a 2d photograph. The Photoshop program doesnt know the red bars are closer, all it sees are pixels.

 

[xena]

that's how balls work.


yea its a bit lopsided. But his red bars are lopsided too.


no. its a 2d photograph. The Photoshop program doesnt know the red bars are closer, all it sees are pixels.

I agree . But it's image is compressed, look at the way it stretches out in Micks post above . You have a much wider image ( the sea) across the whole frame and a much smaller image ( red lines ) so the sea is going to have a much more dramatic effect when compressed. Thought experiment. Swap the sea for the red lines and the red lines would curve and the sea would not.

 

[deirdre]

I agree . But it's image is compressed, look at the way it stretches out in Micks post above . You have a much wider image ( the sea) across the whole frame and a much smaller image ( red lines ) so the sea is going to have a much more dramatic effect when compressed. Thought experiment. Swap the sea for the red lines and the red lines would curve and the sea would not.

nope. GIMP is a free photoshop like program, that is easy to use and lots of tutorial videos online if you cant figure out how to do something.

draw a long blue line, then some short red lines and compress the image. (to make a straight line, make a dot with your paintbrush then hold the shift key and move your mouse to the far side.. it will automatically draw a straight line for you.)

Anyway, you will see that the long blue line needs to be curved somewhat to start.

 

[Clouds Givemethewillies]

Understand that , but if you look ,some of the sea is straight and not curved the sort of bulge is in the middle and less to the outer ,it not even a "even " curve. The objects in front are also much closer and smaller so you would not see them curve. The curve of the sea is not even . IMO it should be .

The curve of the horizon shown in a digital photo should not be part of a circle. It is the interception of the plane of the sensor with the mirror image of the cone formed by the circular base of the horizon circle with the camera at the apex. It is a conec section.
https://www.google.com/url?sa=t&sou...FjAOegQICBAu&usg=AOvVaw1J66v3QL-juMy5Z4nBqBuo

As far as original photo of a level is concerned.

Whether the bubble is off-centre or just the lighting makes it appear that way is not relevant, nor is the evenness of the ground. It was levelled by adjusting the three levelling screws on the head by sighting against the horizon.

You might have missed the important point that the horizon was also photographed at a low altitude with only one variable being changed (altitude). - Same equipment, same place and time, as near as practicable. The full details and the lense check against a known grid were also documented. I will make a scientist yet.

The level was not perfectly straight, nothing is. The best 'proof' would be to digitally subtract the horizons at the two altitudes.

In order to have both the level and horizon reasonably focused the smallest aperature was used, which reduces the resolution. A longer level would have helped, as it would then have been farther from the camera.

There was no locking screw for the tripod rotation, and it was moving in a gusty wind, so I had to take a snap as best I could at the time.

 

[xena]

You compress a real object it will bend or break a phot image compressed will also bend " the larger image of the photo the more you will see this effect" Take a photo of anything that fills up the large part of the photo such as a landscape and it will bend . It won't shrink . The image has to alter ,move .
. You said yourself that the tripod was moving in a gusty wind . So by your own admission it's not perfect is it . It certainly doesn't look perfect to me.

nope. GIMP is a free photoshop like program, that is easy to use and lots of tutorial videos online if you cant figure out how to do something.

draw a long blue line, then some short red lines and compress the image. (to make a straight line, make a dot with your paintbrush then hold the shift key and move your mouse to the far side.. it will automatically draw a straight line for you.)

Anyway, you will see that the long blue line needs to be curved somewhat to start.

But the image is not curved . It's only curved when compressed . The spirit level is not straight and the photographer stated that it was gusty . I'm not one bit convinced . The compression image IMO looks ridiculous as would any similar image compressed and IMO just looks like nonsense.

 

[deirdre]

But the image is not curved . It's only curved when compressed . The spirit level is not straight and the photographer stated that it was gusty .

it's not a spirt level it is just two steel rods taped together. he used them so he could align the horizon within the rod gaps. It doesnt matter if it is gusty or if the steel rods are level... the horizon is centered between them.

Take a photo of anything that fills up the large part of the photo such as a landscape and it will bend .

You repeating yourself is not making what you say anymore true. Straight lines stay straight. and slightly curved lines curve even more in Photoshop/Gimp. They just do.

 

[Rory]

But the image is not curved. It's only curved when compressed.

Did you miss the posts above (#46 and #49), that show that the curve of the horizon is also noticeable before the image is compressed?

 

[xena]

Did you miss the posts above (#46 and #49), that show that the curve of the horizon is also noticeable before the image is compressed?

Yes and i don't see a curve . It looks straight to me , perhaps I need to go to spec savers

 

[Mick West]

Yes and i don't see a curve . It looks straight to me , perhaps I need to go to spec savers

What size screen are you using?

 

[deirdre]

What size screen are you using?

the whole pic doesnt show when you click enlarge.. you have to drag your sliders back and forth. i didnt see a curve either until i saved it and opened it in gimp to try to move the line up closer to the top. Then i realized half the pic (with the little ends) wasnt showing in my browser.

 

[Rory]

Yes and I don't see a curve. It looks straight to me. Perhaps I need to go to Specsavers.

We're talking about this picture here, right?

Click to enlarge, and scroll left and right.

You still don't see a curve?

 

[DavidB66]

In post #57 I mentioned seeing a photograph of the Bonneville Salt Flats, taken from a hillside, showing noticeable curvature of a long straight road. At that time I couldn't find the photograph, but now I have:

Source: https://www.flickr.com/photos/gopher21479/6780533836/

As is to be expected, the curvature is very slight, and to prove that it is due to the curvature of the earth's surface, and not merely a bend or hump in the road, it would be necessary to show that the road is indeed straight, and that the surface of the ground is truly level. Google Earth shows that the road is straight, and there is no variation of more than a metre or so in elevation along the road, but GE's elevation data are not wholly reliable, so further confirmation from survey data would be desirable.

 

[Chris Rippel]

What should the Earth's curvature look like? Here is my thought experiment.

A six foot tall person can see 3 miles in all directions.

So, when facing north, would the 3 miles in front appear higher than the 3 miles at 45 degree angles on each side, so the Earth appears curved?

And if turning 45 degrees to the right, would the 3 miles in front again be higher than the 3 miles than the 45 degrees on each side, so the Earth still appears curved?

Etc. Etc. all the way around the circle?

I think not.

I am skeptical that a horizon higher in front than on the sides is not what Earth's curve would look like. I think we will only see the Earth's curvature horizontally right and left across our view when we are high enough to look down on the Earth.

 

[Mick West]

I am skeptical that a horizon higher in front than on the sides is not what Earth's curve would look like. I think we will only see the Earth's curvature horizontally right and left across our view when we are high enough to look down on the Earth.

How high is high enough?

The curve calculator, in advanced mode will tell you how much the side of an image will dip.
https://www.metabunk.org/curve/?d=4&h=6&r=3959&u=i&a=a&fd=60&fp=3264

The calculations are discussed at length here:
https://www.metabunk.org/are-lynchs-horizon-calculations-correct.t7877/

 

[Laser]

@Chris Rippel - Your thought experiment, or a variation of it, has tricked many globers as well as flat earthers. Stated a little differently, it almost seems to be a mathematical proof that the horizon can't be curved. i.e. A) Eye level is a flat plane through the eye of the observer B) eye level out in the distance appears as a straight line, as it is part of that flat plane. C) The horizon on a spherical ocean is a constant drop below the straight eye level line. D) A line a constant distance from another line is a parallel line. Conclusion: A line, such as the horizon, that is parallel to a straight line must also be a straight line.

Frankly I haven't yet been able to get it completely clear in my head how the horizon manages to appear curved in violation of this seeming proof. But I have come up with a simple thought experiment that makes it clear this proof is unsound.

Imagine setting up something like a theodolite on a tripod on a flat surface, like maybe a basketball court. Imagine painting a circle on the flat surface below the theodolite with a center directly below the theodolite, and a radius such that when the theodolite is tilted down 45degrees below level, then the crosshairs will be on the circle. Now the angular dip below eye level of the circle will be a constant 45deg all around. Yet the curvature of the circle will be plainly visible when viewed from above at 45deg angle. Now if you make a bigger circle, such as one that only requires a 10deg dip of the theodolite, then the curvature of the circle edge should still be visible. And no matter how slight the dip below horizontal, as long as there is at least some dip, you should be looking down at the edge of a curved circle, and thus there should be at least a slight curvature.

 

[Rory]

Also, earlier in this thread there are links to Walter Bislin's site (walter.bislins.ch) where we can simulate what the horizon would look like from any given altitude. It is indeed curved, just as we see in reality.

The idea that it can't be "higher" in the middle than at the edges makes perfect sense - and it isn't. The easiest way for me to imagine the curve of the horizon is to think of it as akin to the edge of a coin. A coin is flat, yet it also has a curved edge, all points of which are at the same "height".

 

[Trailblazer]

The idea that it can't be "higher" in the middle than at the edges makes perfect sense - and it isn't. The easiest way for me to imagine the curve of the horizon is to think of it as akin to the edge of a coin. A coin is flat, yet it also has a curved edge, all points of which are at the same "height".

The problem with this simple analogy is of course that Flat Earthers will then say "So you mean the Earth is flat like a coin?" and we're back where we started! I'm trying to think of a common object that is shaped like a very flat circular dome, like the section of the Earth's surface above the horizon...

 

[Rory]

Maybe a visual, physical representation would be better: take a ball, put a cone on it; the point of the cone is the observer; the rim of the cone forms a circle; that circle is the horizon.

I have also had some success explaining it using a bowl analogy: the bowl is curved, but the rim of the bowl is 'flat' (turn it upside down and place it on a table, etc).

Of course, then you have something that looks like a dome.

I suppose, at the end of the day, if they want to get it, they will - it's not that difficult - and if they don't, they won't.

 

[Antithesis]

It happens that I made a series pictures using the cone analogy while conversing with a flat earther last month.

In the last picture, the white-purple interface is like the horizon from the observer's perspective. I also took away the cone and showed the horizon as just being part of a circle

The flat earther had the curious idea that small angles don't matter and can be ignored. He objected to my diagrams on the grounds that the dip angle of the horizon is too large. He considered Rory's picture with the red bars to be "dead ahead" level, not pointing 0.425 degrees downward (calculation).

My rejoinder was that the angular diameter of the moon is about half a degree, so saying that 0.425 degrees doesn't exist is like saying the moon doesn't exist. (In retrospect it would have been more poignant to say it's like the sun not existing, whose angular diameter is also about half a degree.)

 

[JohnP]

@Chris Rippel - Your thought experiment, or a variation of it, has tricked many globers as well as flat earthers. Stated a little differently, it almost seems to be a mathematical proof that the horizon can't be curved. i.e. A) Eye level is a flat plane through the eye of the observer B) eye level out in the distance appears as a straight line, as it is part of that flat plane. C) The horizon on a spherical ocean is a constant drop below the straight eye level line. D) A line a constant distance from another line is a parallel line. Conclusion: A line, such as the horizon, that is parallel to a straight line must also be a straight line.

Frankly I haven't yet been able to get it completely clear in my head how the horizon manages to appear curved in violation of this seeming proof. But I have come up with a simple thought experiment that makes it clear this proof is unsound.

I tend to have the same difficulty; but then I remind myself that if you go "high" enough, the horizon certainly does look curved--think of the Moon.