DarkStar
Active Member
Spherical Trig Help Needed 
I had posted a blog post about viewing the horizon from high-altitude, roughly based on Lynch's paper 'Visually discerning the curvature of the Earth' -- or so I thought.
One problem with such calculations is we're talking about small quantities and since I had created my calculator in GeoGebra I was pretty confident that the values I were getting were correct so I didn't really test them as carefully as I should have.
A friendly person did a little 'peer-review' and started asking me some questions and I had to agree, something wasn't right. Now, I freely admit that my calculator is just an approximation (to avoid one bit of spherical conversion that doesn't change the end result much) but it should be accurate enough for realistic altitudes (35,000' and maybe a balloon at 120,000'); so I'm not worried about that part so much.
But it turns out I had definitely misunderstood Lynch's intended geometry and after a bit of work I *THINK* I see where we disagree.
So now I'm here looking for additional input and review. Meanwhile, I have flagged that section of my post as under review.
So you can review Lynch's paper and then compare my blog post and see what you think.
I created the diagram below to aid in discussing my model. Please distinguish if you are talking about this 'Darkstar' model or Lynch paper when referring to geometric labels. In this version I made both LOS arc and FOV arc spherical. That's really the only difference with my GeoGebra model (and the way things are labelled a bit).
What I *think* the Lynch model is doing (in terms of this diagram) is pushing points B & C out to the Orange "Earth Circumference" curve, and his X is a function of the FOV (chord C->B) and his S is the sagitta of THAT arc of R=Earth Radius (so rotate that whole YXR triangle and attach to midpoint of B&C and then other end at B (or C doesn't matter).
What makes me suspect this is that in Lynch's paper his S & R are in terms of Earth Circumference -- but his X calculation isn't given so it took some work with another person to sort this out in my mind (wasn't obvious to me).
So the question is -- IF (and that's a big IF) my understand of Lynch is correct -- isn't that the wrong geometry to be using? You cannot see the Earth circumference along that slice EXCEPT at Horizon/D (well, in practice you can't see that either due to atmosphere but we're talking ideal model here).
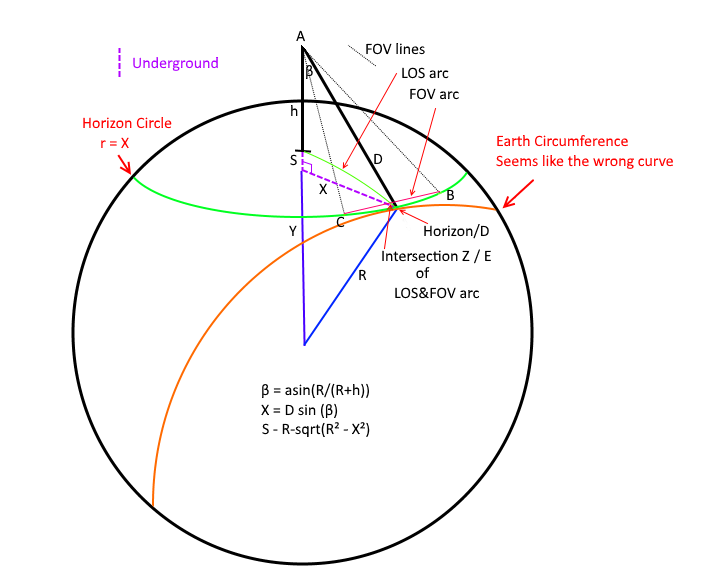
For calculation purposes let's stick to Lynch's example:
h = 35000' (observation height ~6.6288 mi)
R = 3959 mi (approx Earth Radius)
h.FOV ~ 62.7
v.FOV ~ 47.1
In my model I get a very small angle (0.041°) because you can see that the last ~33 miles (which is approximately where points B & C cut across) is almost completely coincident with the views line of sight. The angle between viewer->Z and viewer->horizon here is that 0.041° so that's how much my model says that horizon would be 'stick up' over that B->C chord from our viewpoint.
We both agree on the first few calculations:
(1) first I solve big right triangle for D and β: (R+h)² = R² + D²
(2) D = sqrt(2*R*h + h²) = ~229.196 mi
(3) β = asin(R/(R+h)) ~ 86.687°
(4) α = acos(R/(R+h)) ~ 3.313°
Here we Diverge... for Darkstar model:
X = (D*sin(β)) = 228.81295 mi -- this is the radius of my horizon circle (just a little shorter than D)
And we take the chord B->C, calculate the sagitta of that, and then we take the angular delta along that line of sight -- which is very small because that distance is all very tilted along our line of sight.
Working Lynch backwards he gets ~0.51° -- so that implies...
2*atan(S/D/2) = 0.51° (angular size of S at distance D)
S ~ 2.037 mi (height of sagitta)
S = R - sqrt(R² - X²)
X ~ 126.993 mi
I'm still working on how to calculate his value for X given h.FOV -- I have an idea and it's close to D*tan(h.FOV/2) but I have to adjust for S.
Thoughts?
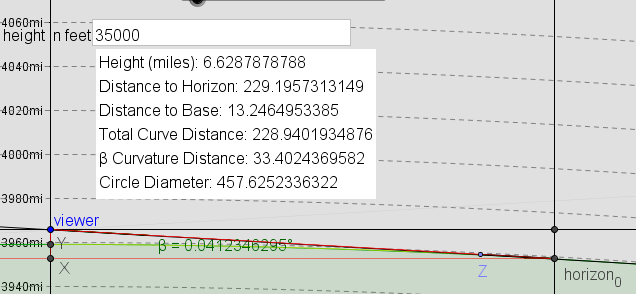
Here is what my side view looks like however and viewer height and the circle of the Earth here are trivially correct so that's an accurate view as far as that goes. You can see how sharp that angle becomes as you get closer to the horizon point. Z here is 33.4 *MILES* (β Curvature Distance) from the horizon. Even if I have everything else wrong human beings are NOT seeing most of that 'distance to the horizon' as more than a tiny smear and an anthill at Z would completely block it
'Circle Diameter' here is that bottom red line. Distance to Base is viewer total distance to the bottom red line (viewer->X), Height is viewer->Y
I had posted a blog post about viewing the horizon from high-altitude, roughly based on Lynch's paper 'Visually discerning the curvature of the Earth' -- or so I thought.
One problem with such calculations is we're talking about small quantities and since I had created my calculator in GeoGebra I was pretty confident that the values I were getting were correct so I didn't really test them as carefully as I should have.
A friendly person did a little 'peer-review' and started asking me some questions and I had to agree, something wasn't right. Now, I freely admit that my calculator is just an approximation (to avoid one bit of spherical conversion that doesn't change the end result much) but it should be accurate enough for realistic altitudes (35,000' and maybe a balloon at 120,000'); so I'm not worried about that part so much.
But it turns out I had definitely misunderstood Lynch's intended geometry and after a bit of work I *THINK* I see where we disagree.
So now I'm here looking for additional input and review. Meanwhile, I have flagged that section of my post as under review.
So you can review Lynch's paper and then compare my blog post and see what you think.
I created the diagram below to aid in discussing my model. Please distinguish if you are talking about this 'Darkstar' model or Lynch paper when referring to geometric labels. In this version I made both LOS arc and FOV arc spherical. That's really the only difference with my GeoGebra model (and the way things are labelled a bit).
What I *think* the Lynch model is doing (in terms of this diagram) is pushing points B & C out to the Orange "Earth Circumference" curve, and his X is a function of the FOV (chord C->B) and his S is the sagitta of THAT arc of R=Earth Radius (so rotate that whole YXR triangle and attach to midpoint of B&C and then other end at B (or C doesn't matter).
What makes me suspect this is that in Lynch's paper his S & R are in terms of Earth Circumference -- but his X calculation isn't given so it took some work with another person to sort this out in my mind (wasn't obvious to me).
So the question is -- IF (and that's a big IF) my understand of Lynch is correct -- isn't that the wrong geometry to be using? You cannot see the Earth circumference along that slice EXCEPT at Horizon/D (well, in practice you can't see that either due to atmosphere but we're talking ideal model here).

For calculation purposes let's stick to Lynch's example:
h = 35000' (observation height ~6.6288 mi)
R = 3959 mi (approx Earth Radius)
h.FOV ~ 62.7
v.FOV ~ 47.1
In my model I get a very small angle (0.041°) because you can see that the last ~33 miles (which is approximately where points B & C cut across) is almost completely coincident with the views line of sight. The angle between viewer->Z and viewer->horizon here is that 0.041° so that's how much my model says that horizon would be 'stick up' over that B->C chord from our viewpoint.
We both agree on the first few calculations:
(1) first I solve big right triangle for D and β: (R+h)² = R² + D²
(2) D = sqrt(2*R*h + h²) = ~229.196 mi
(3) β = asin(R/(R+h)) ~ 86.687°
(4) α = acos(R/(R+h)) ~ 3.313°
Here we Diverge... for Darkstar model:
X = (D*sin(β)) = 228.81295 mi -- this is the radius of my horizon circle (just a little shorter than D)
And we take the chord B->C, calculate the sagitta of that, and then we take the angular delta along that line of sight -- which is very small because that distance is all very tilted along our line of sight.
Working Lynch backwards he gets ~0.51° -- so that implies...
2*atan(S/D/2) = 0.51° (angular size of S at distance D)
S ~ 2.037 mi (height of sagitta)
S = R - sqrt(R² - X²)
X ~ 126.993 mi
I'm still working on how to calculate his value for X given h.FOV -- I have an idea and it's close to D*tan(h.FOV/2) but I have to adjust for S.
Thoughts?
Here is what my side view looks like however and viewer height and the circle of the Earth here are trivially correct so that's an accurate view as far as that goes. You can see how sharp that angle becomes as you get closer to the horizon point. Z here is 33.4 *MILES* (β Curvature Distance) from the horizon. Even if I have everything else wrong human beings are NOT seeing most of that 'distance to the horizon' as more than a tiny smear and an anthill at Z would completely block it
'Circle Diameter' here is that bottom red line. Distance to Base is viewer total distance to the bottom red line (viewer->X), Height is viewer->Y


