Hello
@Kaen ! Thank you so much for that diagram above. It is really helpful to explain parallax effect to those unfamiliar with it.
However, before I ask you questions I have about the assumptions made in the diagram, I would like to drop back and punt because I just discovered on FB Bruce Maccabee's Original calculations made on March 9. (You operated only from his revised calculations dated March 12.) Here is the text of his original calculations. Does it give you any more insight into his process? It looks like his original calculations were more in line with yours, but then I suppose he revised his calculations because it wasn't fitting the original narrative of TTSA that the object must be moving fast 380 Kn at a low altitude of 100 ft)
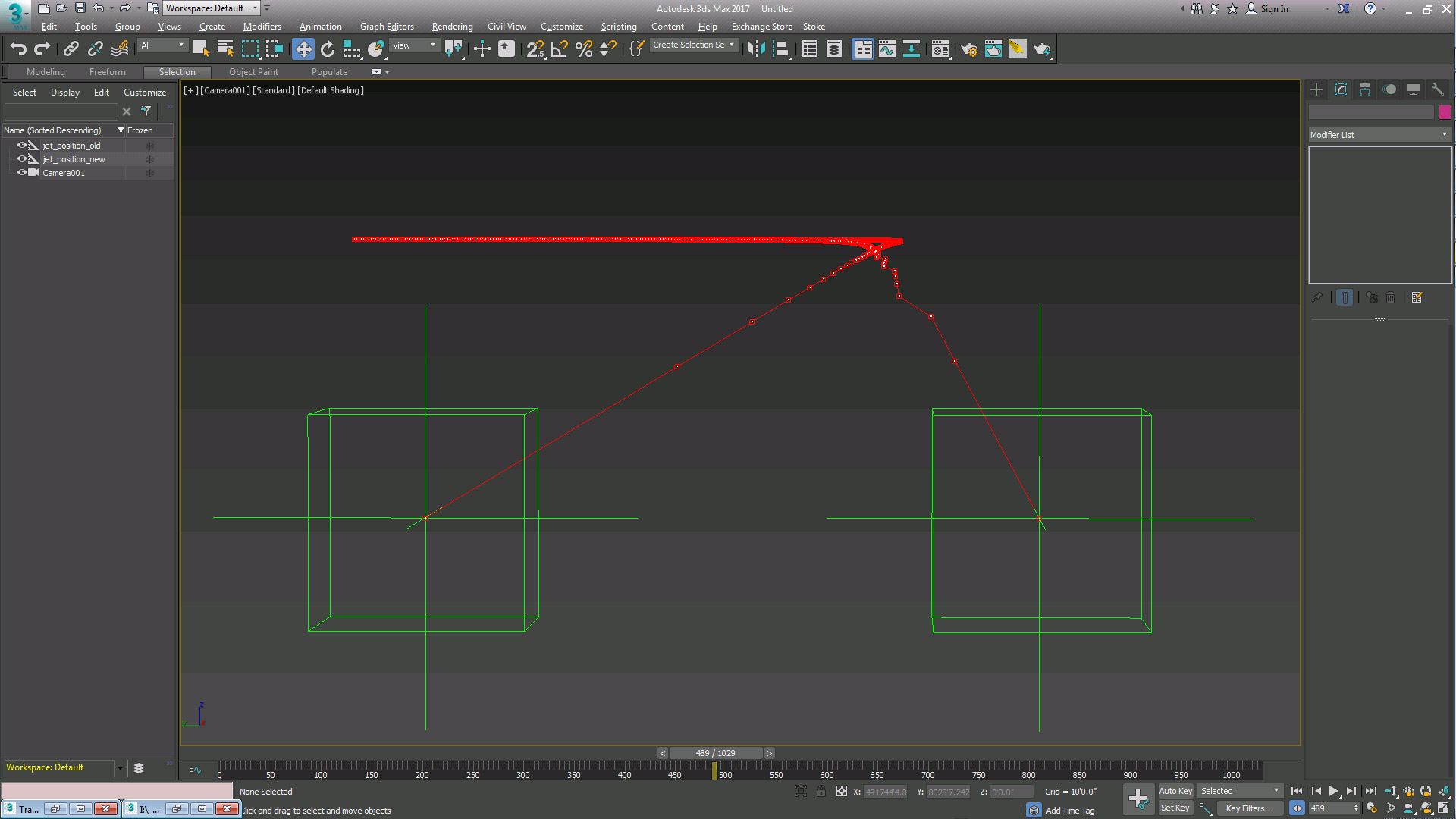
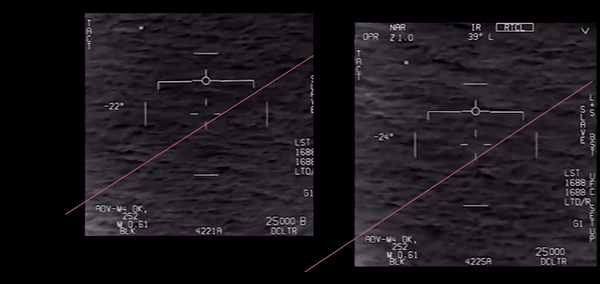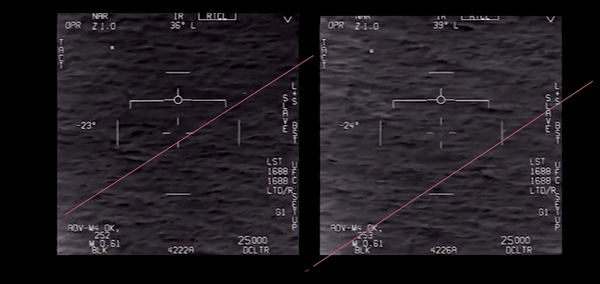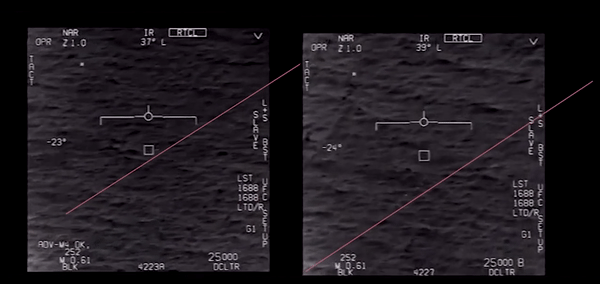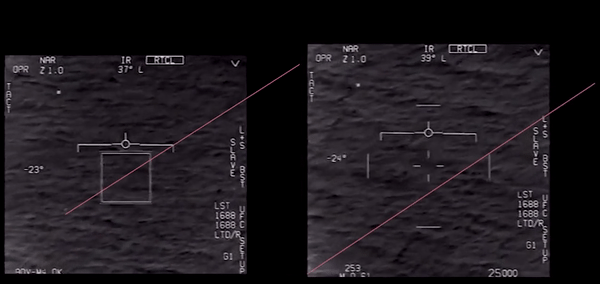
Bruce probably based his calculations on a period in the video above where the object crosses the display while the ATFLIR is more or less fixed on the same patch of sea. This is the period from 5,5 s – 7,3 s (duration 1,8 s).
The picture below contains the snapshots of the object entering and leaving the FOV. I projected the object's end position in the first picture, taking a slight shift of the camera into account (the white rectangle shows the same patch of sea). From these two positions I calculated the percentage of the ATFLIR FOV that the object crossed in these 1,8 seconds.
Let's go through Bruce's calculations step by step:
External Quote:
Object altitude calculated as: (4.1 nm [height of plane] – (4.1 slant range [plane to object]) x sin 22 = 4.1 – 1.54 = 2.46 below airplane altitude;
[Later he changes the 4,1 nm to 4,5 nm:] The exact distance to the object at that time is not known because the system had not yet locked on. However when it did lock on a short time later the range was about 4.1 nm and decreasing. I therefore "guesstimate" the range at 4.5 nm.
The calculated 2,46 nm is not a 'below airplane altitude' but the actual object altitude.
During Bruce's 1,8 s period, the object slant vector is at a downward angle of 24 degrees, not 22.
Slant range is unknown at that time, but can be estimated: At 12 s it is 4,4 nm and decreasing with 0,1 nm per 1,8 s. So at 6 s in the video the estimated slant range would be 4,4 + (0,1 x 6/1,8) = 4,7 nm, not 4,1 (later 4,5).
This gives an altitude difference between jet and object of 4,7 x sin(24) = 1,9 nm.
Jet is at 4,1 nm altitude so object is at 4,1 – 1,9 = 2,2 nm altitude (13.300 feet), not 2,46.
External Quote:
At 4.1 nm range to the object, the distance across the 1.5 deg FOV is (4.1nm) x [1.5 deg x 0.0174 rad/deg]= 0.1 nm.
[Later he corrects this value for the new range of 4,5 nm:] The width of the FOV is 1.5 deg x 0.0174 rad/deg = 0.026 rad which corresponds to 0.117 nm at 4.5 nm distance.
The actual range is closer to 4,7 nm (see above). This gives 0,12 nm instead of 0,1 (later 0,117 nm).
I wonder whether the 1,5 degrees FOV is correct. I thought this was the FOV at zoom level 2, it may be 0,3 degrees at zoom level 1. This would double the value to 0,24 nm
External Quote:
It crosses the FOV at about a 45 deg angle so the actual approximate distance across the FOV is 0.1 nm/0.707 = 0.14 nm;
[Later he corrects this value for the new range of 4,5 nm:] The object crossed the FOV area at an angle of about 45 deg so the distance traveled as it crossed the FOV was about (0.026 rad) x 1.41(to account for the 45 degree crossing) x 4.5 nm = 0.165 nm.
I made a more accurate estimate of the FOV coverage (see picture above), it is 1,31 so the total distance is 1,31 x 0,12 = 0,16 nm instead of 0,14 (later 0,165 nm).
External Quote:
it crosses in 4 to 3 sec implying a differential speed of the plane and object of 0.14 nm/ ( 4 to 3 sec)/(one hour/ 3600) = 126 to 170 kt)…
[Later he corrects this value to 1,8 s and the speed to 330 kt:] I found that it took about 55 frames at 30 frames/ sec which corresponds to 55/30 = 1.8 sec. It traveled this distance in about 1.8 sec for a speed of 0.092 nm/sec which is about 330 kt....about twice the larger speed previously calculated but certainly not an earth shaking speed.
With the 0,16 instead of 0,165 nm this yields a differential speed of 0,16/1,8 = 0,089 nm/s = 316 kt instead of 330 kt, so very close to Bruce's value.
External Quote:
Since the plane is going at about 250 kt the object was going at the speed approx. (250 – 150) = 100 kt in the same direction as the airplane but clearly slower)calculation assumes land speed is approx. same as air speed) )))
The 330 kt is a
differential speed and needs to be compensated for the parallax effect. Here, Bruce makes some crude approximations using the CAS of the jet, and assuming the parallax compensation equals the jet speed.
In reality the parallax compensation is 0,52 x the jet speed (see my post about the parallax). The camera shifts a little (about 16% of the FOV) along with the object's trajectory while the object passes. This will add an additional 16% to the parallax compensation speed that I estimated (267 kt instead of 230 kt).
Note that the speed in the ATFLIR display being CAS is solely based on the annotations in the video made by TTSA. Maybe TTSA was wrong and the speed is based on something else like GPS data.
A few additional remarks:
The assumed FOV of the ATFLIR is 1,5 degrees. It may be twice that, i.e., the narrow FOV of an ATFLIR is 3 degrees according this document:
https://www.forecastinternational.com/archive/disp_old_pdf.cfm?ARC_ID=452
That would double the computed differential speed of the object to approximately 650 knots. This speed no longer implies a bird or balloon, and it no longer complies with the speeds computed earlier in this thread.
The object seems to travel
against the direction of the jet, while other calculations made in this thread indicate it travels in the opposite direction. This is odd.