from numpy import *
from pylab import *
from scipy.interpolate import *
################################################################################
## constants
################################################################################
G = 9.8 ## m/s^2
NMI = 1852.
HOUR = 3600.
DEG = pi / 180.
KTS = NMI / HOUR
FEET = FOOT = .3048
################################################################################
## raw data
################################################################################
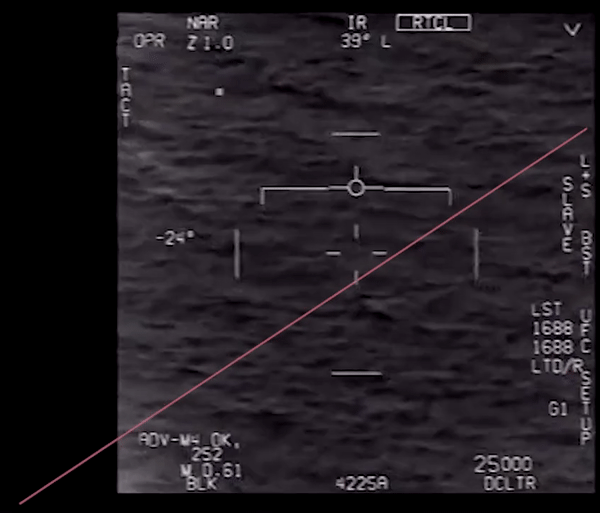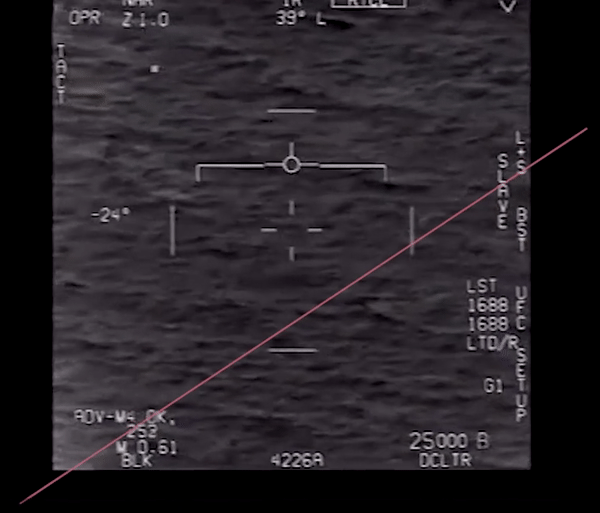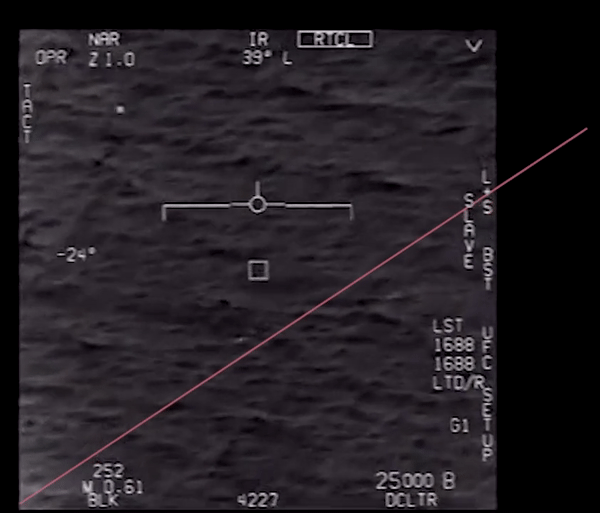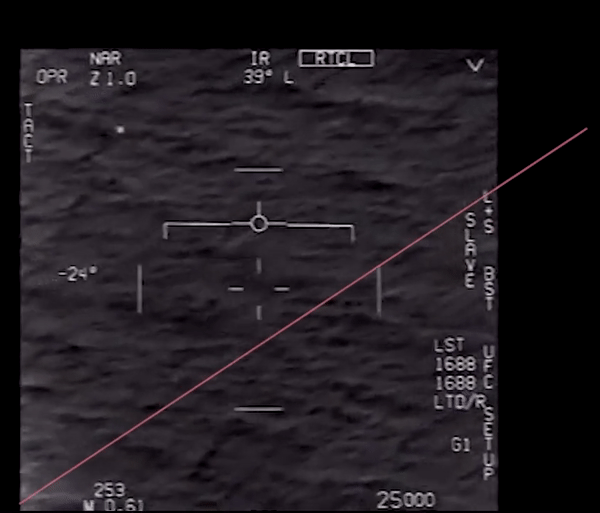
txt = 'goFastRoll.txt'
roll_data = loadtxt(txt, skiprows=1)
# t sec az deg, el deg, range nmi v?
az_data = array([
[12 + 10./30, -43],
[13 + 10./30, -44],
[13 + 20./30, -45],
[14 + 19./30, -46],
[15 + 13./30, -47],
[16 + 13./30, -48],
[18 + 0./30, -49],
[21 + 6./30, -50],
[23 + 6./30, -51],
[24 + 18./30, -52],
[26 + 6./30, -53],
[27 + 18./30, -54],
[29 + 6./30, -55],
[30 + 13./30, -56],
[31 + 19./30, -57],
[32 + 25./30, -58],
[33 + 0./30, -58]
])
el_data = array([
[12 + 10./30, -26],
[13 + 19./30, -27],
[16 + 6./30, -28],
[18 + 25./30, -29],
[21 + 7./30, -30],
[23 + 13./30, -31],
[25 + 25./30, -32],
[28 + 1./30, -33],
[30 + 1./30, -34],
[32 + 7./30, -35],
[33 + 0./30, -35]
])
rng_data = array([
[12 + 10./30, 4.4],
[13 + 10./30, 4.3],
[15 + 3./30, 4.2],
[17 + 4./30, 4.1],
[19 + 1./30, 4.0],
[20 + 29./30, 3.9],
[22 + 28./30, 3.8],
[24 + 28./30, 3.7],
[27 + 1./30, 3.6],
[29 + 13./30, 3.5],
[31 + 22./30, 3.4],
[33 + 0./30, 3.4],
])
az = interp1d(az_data[:,0], az_data[:,1])
el = interp1d(el_data[:,0], el_data[:,1])
rng = interp1d(rng_data[:,0], rng_data[:,1])
roll = interp1d(roll_data[:,0], -roll_data[:,1])
dt = .1
t = arange(15, 30, dt)
N = len(t)
## align data to uniform time grid and standard units
data = vstack([az(t) * DEG, el(t) * DEG, rng(t) * NMI, roll(t) * DEG]).T
################################################################################
## functions
################################################################################
def get_accel(roll):
'''
assume a corrdinated turn so that accel vector (with gavity) is orthog to wings
'''
return -tan(roll) * G
################################################################################
## Numerical Integration of accel to get vel and pos
################################################################################
for WIND_HDG in arange(225, 226, 45) * DEG:
# xoWIND_HDG = 90 * DEG
WIND_SPD = 100 * KTS
WIND_VEL = array([cos(WIND_HDG), -sin(WIND_HDG), 0]) * WIND_SPD
AIR_SPEED = 369 * KTS
pos = array([0, 0, 25000 * FEET])
vel = array([AIR_SPEED, 0, 0]) + WIND_VEL
poss = [] ### save track
vels = [] ### save vel
Xs = []
R = array([0, 0, 1]) ### unit up vector (assume minimal earth curvature over)
for i in range(N):
rho = data[i, 3] ## grab roll
I = vel - dot(R, vel) * R; I = I / linalg.norm(I) ## intrack vector
L = array([-I[1], I[0], 0]) ## horizontal unit left vector
a = get_accel(rho) * L
dv = a * dt
vel = vel + dv
# vel = GND_SPEED * vel / linalg.norm(vel)
dp = vel * dt
pos = pos + dp
C = cross(R, I)
RIC_X = vstack([R, I, C]).T
RHO_X = array([[cos(rho), 0, -sin(rho)],
[ 0, 1, 0],
[sin(rho), 0, cos(rho)]])
X = RIC_X @ RHO_X ## include roll
X = RIC_X ### dont include roll
poss.append(pos)
vels.append(vel)
Xs.append(X)
poss = array(poss)
vels = array(vels)
Xs = array(Xs)
azs = data[:,0]
els = data[:,1]
rngs = data[:,2]
### compute 3d position of unknown object
x = cos(azs) * cos(els)
y = -sin(azs) * cos(els)
z = sin(els)
doas = vstack([z, x, y]).T
d_fixed = array([X @ d for X, d in zip(Xs, doas)])
gs = poss + d_fixed * rngs[:,newaxis]
figure(123); plot(linalg.norm(abs(diff(gs, axis=0)), axis=1) / dt / KTS)
################################################################################
## PLOTS
################################################################################
figure(1)
ax = subplot(411)
plot(t, az(t))
plot(az_data[:,0], az_data[:,1])
ylabel('Az [deg]')
subplot(412)
plot(t, el(t))
plot(el_data[:,0], el_data[:,1])
ylabel('El [deg]')
subplot(413)
plot(t, rng(t))
plot(rng_data[:,0], rng_data[:,1])
ylabel('Rng [nmi]')
subplot(414)
plot(t, roll(t))
plot(roll_data[:,0], -roll_data[:,1])
ylabel('Roll [deg]')
xlabel('Time [sec]')
figure(2)
plot(-poss[:,1] / NMI, poss[:,0] / NMI)
plot(-gs[:,1] / NMI, gs[:,0] / NMI)
xlabel('<-- Port [nmi] Starboard-->')
ylabel('Intrack [nmi] -->')
axis('equal')
## try 3D plot... don't error out if libs not present
try:
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(3)
ax = fig.gca(projection='3d')
# ax.plot(-poss[:,1] / NMI, poss[:,0] / NMI, poss[:,2] / FEET)
ax.plot(-gs[:,1] / NMI, gs[:,0] / NMI, gs[:,2] / FEET)
except:
pass
show()
ROLL DATA, save as "goFastRoll.txt"