Z.W. Wolf
Senior Member.
Over the course of a year Flat Earth Believer Dave Marsh made observations of the Moon and collected data from the site Time and Date.
From YT video Flat Earth: Moon Race
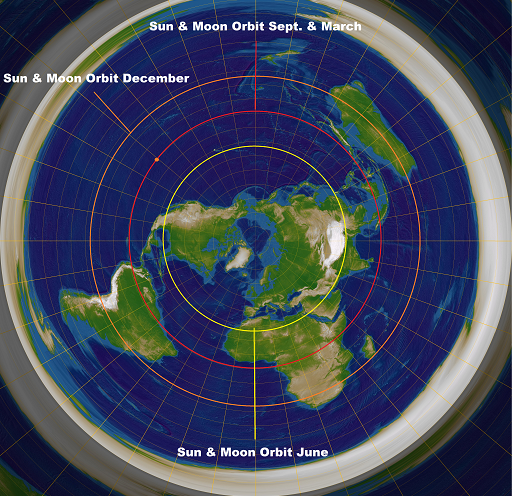
The Sun moves in a spiral. It's clear that the Sun has to move faster when it's over the Tropic of Capricorn than it does when it's over the Tropic of Cancer.
On FE, Cancer is a smaller circle closer to the North Pole. Capricorn is a larger circle on the far side of the equator.
On SE, Cancer is north of the equator and Capricorn is south.
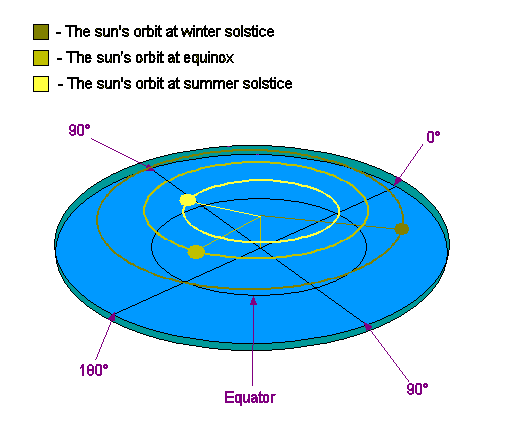
His hypothesis: The Moon will travel faster when it is over the Tropic of Capricorn than it will when it is over the Tropic of Cancer; and at a speed in between the two when it is over the equator. This difference in speed should be measurable.
Method: Marsh set up his camera in his garden (that's "yard" to us Yanks) and videoed the Moon at calculated times. He was careful to use the same zoom factor each time. He then measured how long it took the Moon to travel across the frame in each video. The elapsed time is correlated with the Moon's proper motion - its true speed over the surface of the Earth.
Oddly, he chose to do this during each lunar month over the year, seemingly never considering that in the FE model he was supposed to be testing, the Moon is over each latitude only once per year.
He chose a cycle based on the inclination of the Moon’s orbit in the SE model. Referring to various online resources, he found the Moon’s altitude above his local horizon at the time the Moon passed his local meridian, and did this on each day during a particular lunar month. He labeled the highest altitude he could find “Cancer,” the lowest “Capricorn,” and the middlemost “Equator.” He considered this the days when the Sun was over these particular latitudes on the surface of the FE. Once again never considering that he was muddling the FE and SE models.
An example:
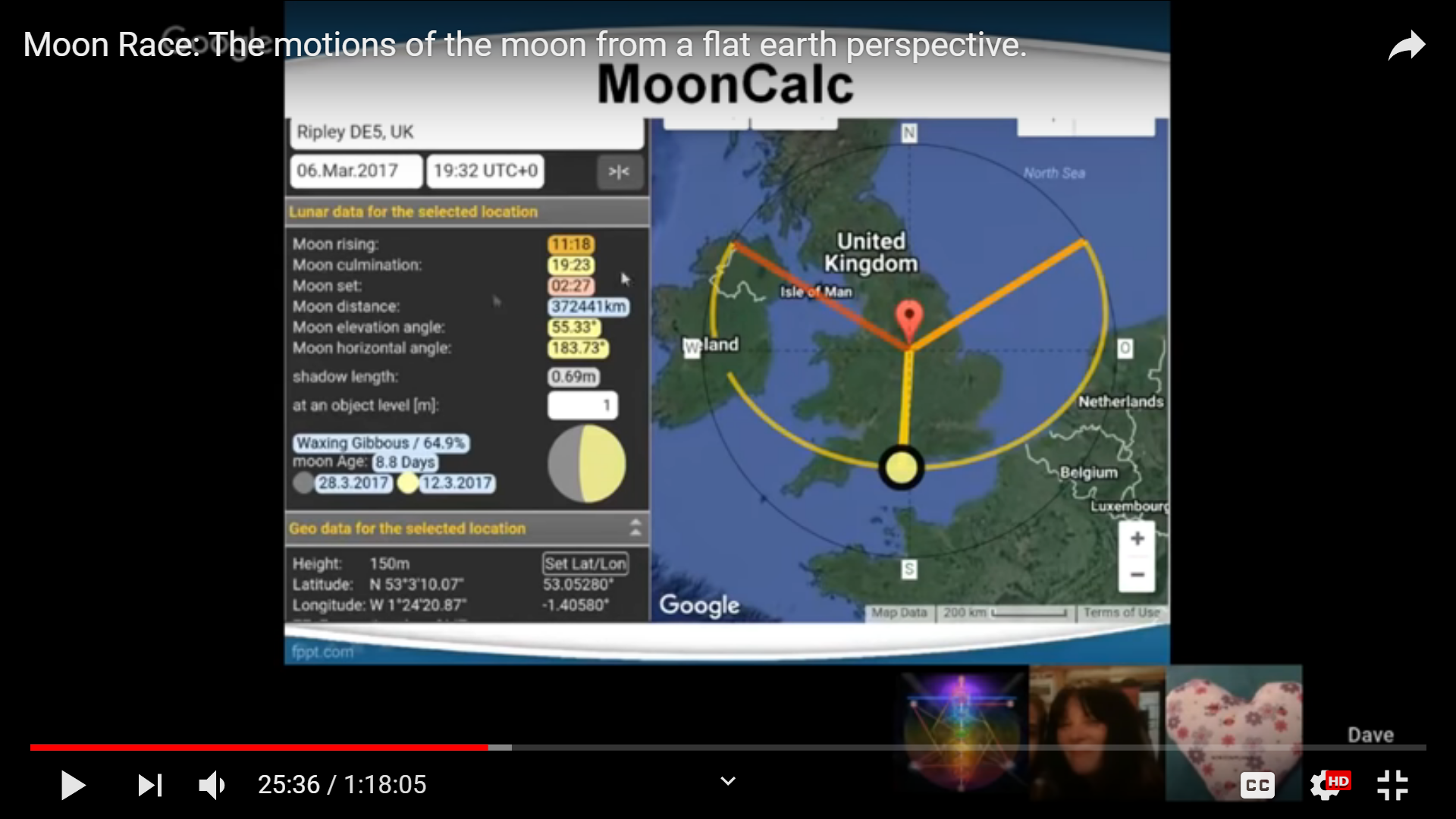
He considers this the day in this lunar month when the Moon is over the Tropic of Cancer, because this is the highest altitude he can find during the month.
(Note: He mistakenly labels altitude as “declination” in his charts.)
In his video, Moon Race: The motions of the moon from a flat earth perspective, Marsh shows us his videos during March and during August/September:
March

The lighted side of the Moon "in Capricorn" is just entering the frame. Marsh has estimated the time when the unlit edge entered the frame and estimated the time when the unlit edge touched the right edge of the frame. I suspect this has caused a problem.
August

This time the Moon "in Cancer" is the one with the dark leading edge.
For March, Marsh doesn’t note his estimated elapsed times for the Moon to completely cross the frame - just ordinal numbers:
Mar 7 - Cancer - 2nd
Mar 12 - Equator - 1st
Mar 21 Capricorn - 3rd
There isn't much difference between the three.
He’s surprised that Capricorn is the slowest. He does mention that this is against his expectations for the FE map (the AE map) , but doesn’t expand on this other than noting that this is “quite interesting.”
In Aug/Sept he notes these estimated elapsed times in minutes and seconds (not clock time):
Aug. 5 - Equator 5:20
Aug. 11 - Capricorn: 5:36
Sept 13 Cancer: 6:15
(Marsh had to wait one extra lunar cycle due to being clouded out on Aug. “Cancer date”.)
Marsh is excited that the Moon "in Cancer" "takes forever" to cross the frame. (Capricorn is once again not the fastest.)
Marsh is convinced there is some cycle he's observing, even though in this limited data set there doesn’t seem to be any pattern, except one he wouldn’t like. I made these charts:
The columns are: Ordinal number, time when Moon passed meridian, declination, altitude, distance from Earth, and Moon phase in relation to the movement across the camera frame.
March 7 - Cancer 2nd Time 20:21 Del +17 57 Alt 55.24 Dis 374,548 Km Leading Edge Lit
March 13 - Equator 1st Time 00:36 Del -1 45 Alt 39.25 Dis 390,364 Km Leading Edge Lit
March 21 -Capricorn 3rd Time 6:40 Del -19 47 Alt 17.23 Dis 400,533 Km Leading Edge Dark
August 5 - Capricorn 2nd 23: 47 Dec -19 37 Alt 17.4 Dis 400,262 Lit
August 11 - Equator 1st 3:49 Dec +4 11 Alt 32.9 Dis 383,419 Slightly dark
Sept 13 - Cancer 3rd 5:59 Dec +15 33 Alt 52.56 Dis 393,922 Dark
By ordinal number:
March
1st 00:36 - middle 390,364 middle -1.45 middle
2nd 20:21 earliest 374,548 closest +17 57 highest
3rd 6:40 latest 400,533 farthest -19 47 lowest Leading Edge Dark
August
1st 3:49 middle 383,419 closest +4 11 middle Leading Edge Slightly Dark
2nd 23:37 earliest 400,262 farthest -19 37 lowest
3rd 5:59 latest 393,922 middle +15 33 highest Leading Edge Dark
The only meaningful correlation is Moon phase. When the leading edge was dark, Marsh measured the time to pass through the frame as greatest (and Moon speed as slowest).
In March this was Capricorn, and in Aug/Sept this was Cancer.
I consider the variations in the estimated elapsed times Marsh is presenting as nothing more than measurement error. When the leading edge of the Moon is unlit Marsh has guessed when the leading edge first enters the frame and the moment it touches the right side of the frame. When the leading edge of the Moon was unlit he should have noted when the trailing (lighted) edge was touching the left side of the frame, and when the trailing edge exited the right side of the frame.
I can’t do that because he doesn’t show this. His Moon images just pop out when he thinks the leading edge has touched the right side of the frame.
It’s been pointed out by many people that what Marsh was really seeing was the apparent motion of the Moon due to the Earth’s rotation. Marsh is assuming that he's seeing the ground speed of the Moon over the surface of the FE, without considering the SE model. In the FE model one assumes the observer is motionless and all motions of the Moon would be proper motions. In the SE model the observer is in motion and the Moon is also in motion. Proper motion and apparent motion have to be sorted out; which isn’t easy.
(Even assuming the FE model, Marsh would still have to take distances and perspective into account, which he didn't. He would also have to assume he could measure a difference in speed with his method.)
This is why I'm convinced the varying times are due to measurement error. The apparent motion of the Moon due to orbital speed - and there is such a difference, as I'll show later - is so negligible over a period of just a few minutes that it would not be measurable with Marsh's method in either the SE or FE model.
Marsh made a fundamental error. He assumed the FE model and never considered the SE model.
Assumption: The observer is not moving.
Conclusion: All motion of the Moon observed is proper motion.
Even though Marsh didn't find what he expected - the Moon "over" the Tropic of Capricorn will always be the fastest - he was still convinced that he was seeing some difference in the speed of the Moon, and he sought out evidence of this with a different method. He used data from the site Time and Date and laboriously made charts of his own.
These two -below- show the times the Moon crossed the local meridian in Indonesia, which Marsh uses as an example of how the Moon would act with the observer on the equator.
He's noting the times that the Moon crossed the local meridian. It's well known that the Moon rises 50 minutes later every day on average; but there is a great deal of variation. Marsh is noting the same variation in meridian crossing; which is valid. He's charting the variation in minutes. He has found a cycle which he highlights in yellow.
He produces a chart, which people have noted looks like a heartbeat on an EKG readout.
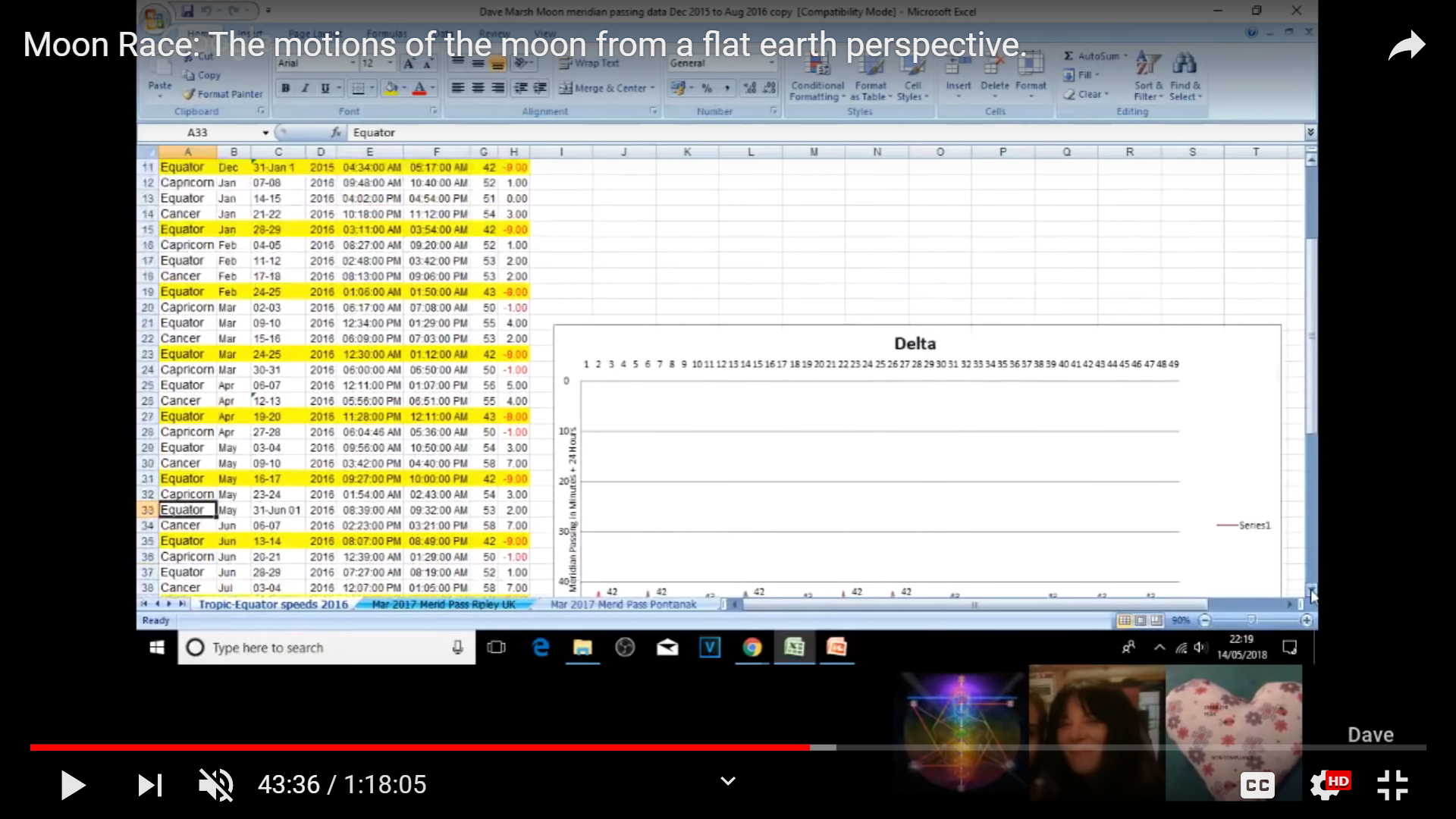
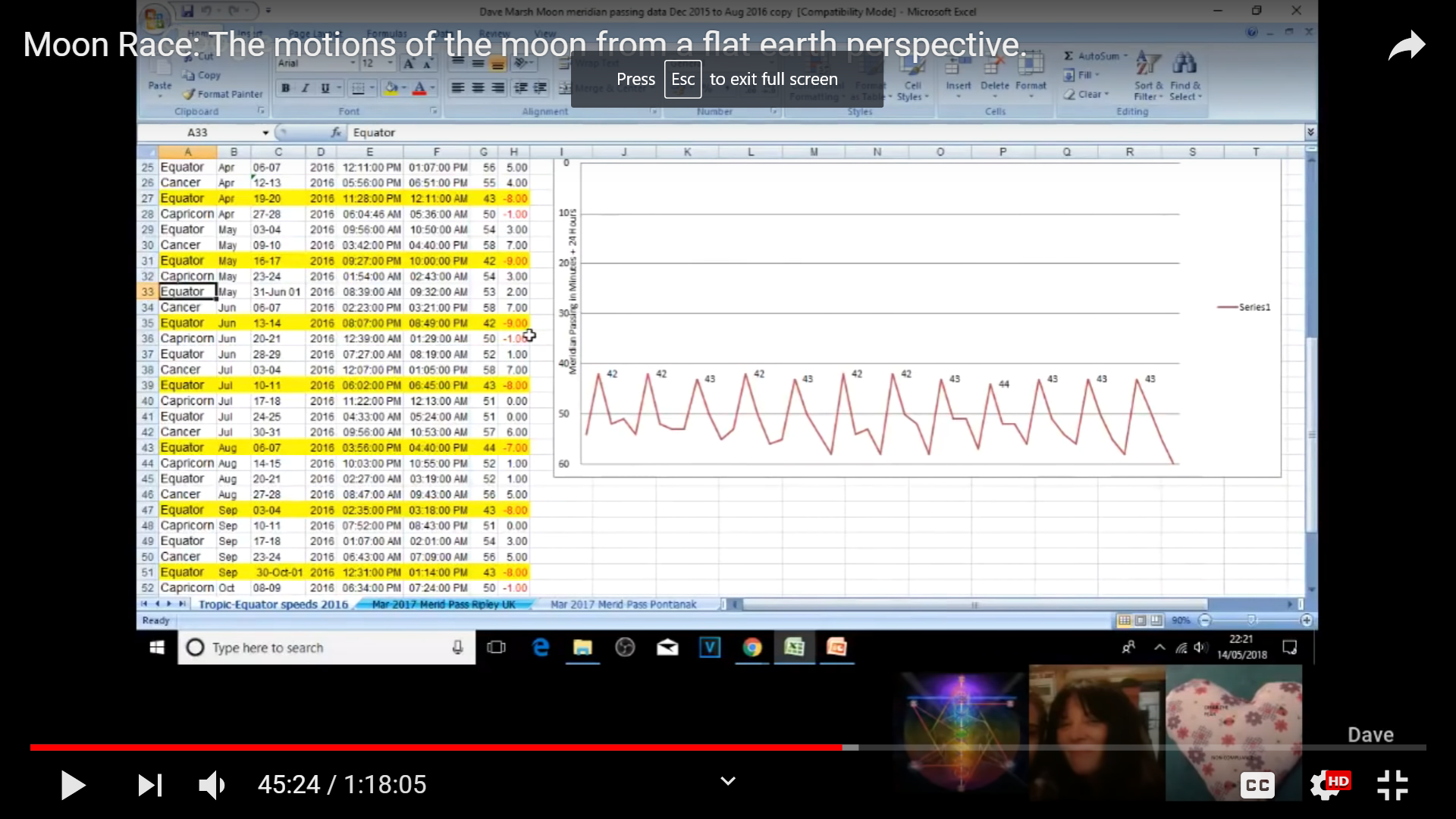
What he has found is the anomalistic month - the mean time of the moon's revolution from perigee to perigee again. You can see that his highlighted dates correlate with the apogee dates for 2106. Note that there are 12 cycles. Why would there be 12 cycles on a FE?
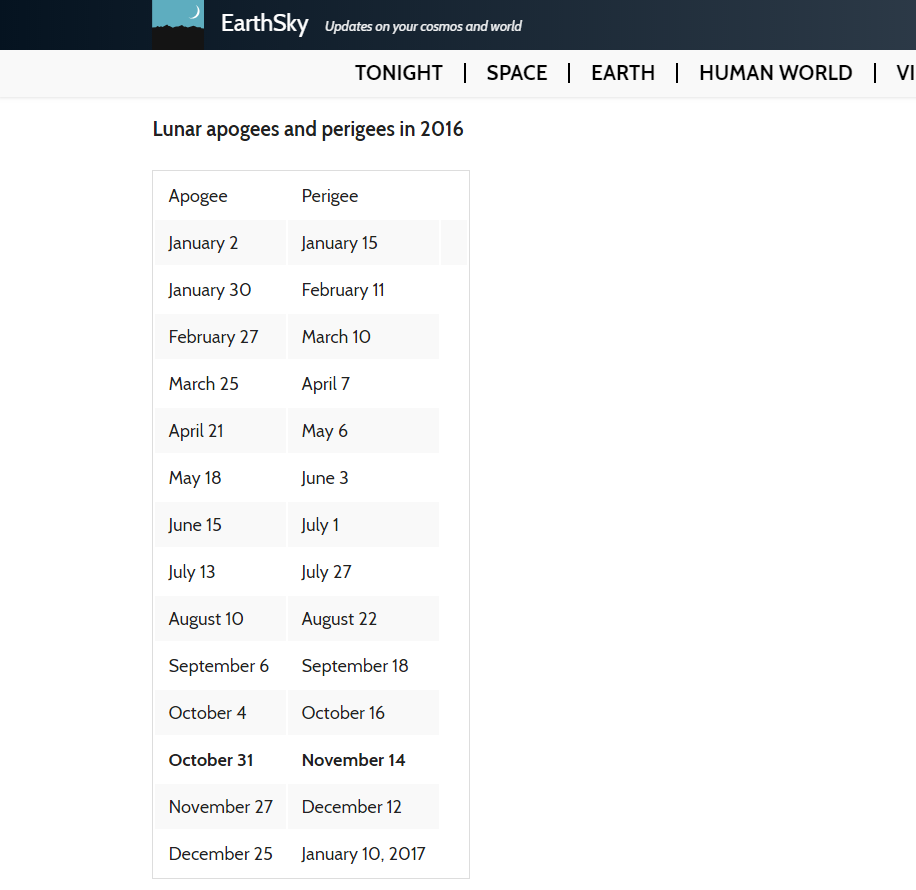
https://en.wikipedia.org/wiki/Lunar_month#Anomalistic_month
The anomalistic month has almost the same period as the synodic month. Marsh mistakenly believes he's found a cycle tied to when the Moon "moves from Cancer to the equator." But this is just a coincidence. The change in the declination (and also altitude) of the Moon is due to the Earth's relation to the inclined orbit of the Moon during a synodic month. The change in the Moon's elapsed time from meridian crossing to next meridian crossing is due to when the Moon is at apogee and perigee in its orbit. They were in this particular relation in 2016, but will slowly move away from this over time.
The elapsed time from lunar meridian crossing to next meridian crossing is least when the Moon is at apogee, and greatest when it is at perigee. An explanation for why this is so highlights the importance of understanding proper and apparent motions.
In Marsh's mind, the decreasing number of minutes from one meridian crossing to the next means that the Moon is traveling faster. It's actually the opposite.
Apogee: The point at which the orbiting body is farthest from the Earth. The "top" of the orbit.
Perigee: Closest.
Orbiting bodies move fastest at perigee and slowest at apogee.
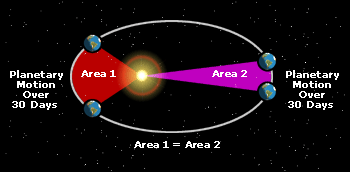
When the Moon is at apogee in its orbit, it is farthest from the Earth; on the left in this illustration. It travels slowest in its orbit at apogee.
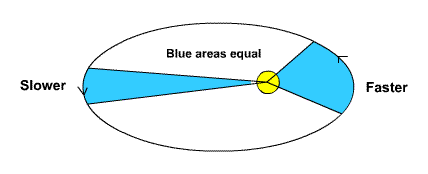
This next illustration - below - shows the Earth around the Sun; but imagine it's the Moon around the Earth. The Earth rotates on its axis counterclockwise and the Moon orbits counterclockwise.
When the Moon orbits faster at perigee (on the left in this illustration) it moves more miles in its orbit during one Earth day. The Earth's rotation has to "catch up" more. Therefore it takes more time for the Moon to move through our sky.
When the Moon is moving slower at apogee it travels less distance in its orbit. The Earth's rotation doesn't have to catch up as much. Therefore the Moon takes less time to move through our sky.
At perigee:
Proper motion: Faster
Apparent motion to observer on Earth: Slower
At apogee:
Proper motion: Slower
Apparent motion to observer on Earth: Faster
From YT video Flat Earth: Moon Race
He's assuming this FE model of Sun movement - an explanation of seasons due to Sun movement.Using the Zetetic method, I set out to record the Moon when it was over the Tropics and on the equator. If the Moon was orbiting above stationary Earth it would need to speed up as it shifted south to cover more ground.

The Sun moves in a spiral. It's clear that the Sun has to move faster when it's over the Tropic of Capricorn than it does when it's over the Tropic of Cancer.

On FE, Cancer is a smaller circle closer to the North Pole. Capricorn is a larger circle on the far side of the equator.
On SE, Cancer is north of the equator and Capricorn is south.

His hypothesis: The Moon will travel faster when it is over the Tropic of Capricorn than it will when it is over the Tropic of Cancer; and at a speed in between the two when it is over the equator. This difference in speed should be measurable.
Method: Marsh set up his camera in his garden (that's "yard" to us Yanks) and videoed the Moon at calculated times. He was careful to use the same zoom factor each time. He then measured how long it took the Moon to travel across the frame in each video. The elapsed time is correlated with the Moon's proper motion - its true speed over the surface of the Earth.
Oddly, he chose to do this during each lunar month over the year, seemingly never considering that in the FE model he was supposed to be testing, the Moon is over each latitude only once per year.
He chose a cycle based on the inclination of the Moon’s orbit in the SE model. Referring to various online resources, he found the Moon’s altitude above his local horizon at the time the Moon passed his local meridian, and did this on each day during a particular lunar month. He labeled the highest altitude he could find “Cancer,” the lowest “Capricorn,” and the middlemost “Equator.” He considered this the days when the Sun was over these particular latitudes on the surface of the FE. Once again never considering that he was muddling the FE and SE models.
An example:

He considers this the day in this lunar month when the Moon is over the Tropic of Cancer, because this is the highest altitude he can find during the month.
(Note: He mistakenly labels altitude as “declination” in his charts.)
In his video, Moon Race: The motions of the moon from a flat earth perspective, Marsh shows us his videos during March and during August/September:
March

The lighted side of the Moon "in Capricorn" is just entering the frame. Marsh has estimated the time when the unlit edge entered the frame and estimated the time when the unlit edge touched the right edge of the frame. I suspect this has caused a problem.
August

This time the Moon "in Cancer" is the one with the dark leading edge.
For March, Marsh doesn’t note his estimated elapsed times for the Moon to completely cross the frame - just ordinal numbers:
Mar 7 - Cancer - 2nd
Mar 12 - Equator - 1st
Mar 21 Capricorn - 3rd
There isn't much difference between the three.
He’s surprised that Capricorn is the slowest. He does mention that this is against his expectations for the FE map (the AE map) , but doesn’t expand on this other than noting that this is “quite interesting.”
In Aug/Sept he notes these estimated elapsed times in minutes and seconds (not clock time):
Aug. 5 - Equator 5:20
Aug. 11 - Capricorn: 5:36
Sept 13 Cancer: 6:15
(Marsh had to wait one extra lunar cycle due to being clouded out on Aug. “Cancer date”.)
Marsh is excited that the Moon "in Cancer" "takes forever" to cross the frame. (Capricorn is once again not the fastest.)
Marsh is convinced there is some cycle he's observing, even though in this limited data set there doesn’t seem to be any pattern, except one he wouldn’t like. I made these charts:
The columns are: Ordinal number, time when Moon passed meridian, declination, altitude, distance from Earth, and Moon phase in relation to the movement across the camera frame.
March 7 - Cancer 2nd Time 20:21 Del +17 57 Alt 55.24 Dis 374,548 Km Leading Edge Lit
March 13 - Equator 1st Time 00:36 Del -1 45 Alt 39.25 Dis 390,364 Km Leading Edge Lit
March 21 -Capricorn 3rd Time 6:40 Del -19 47 Alt 17.23 Dis 400,533 Km Leading Edge Dark
August 5 - Capricorn 2nd 23: 47 Dec -19 37 Alt 17.4 Dis 400,262 Lit
August 11 - Equator 1st 3:49 Dec +4 11 Alt 32.9 Dis 383,419 Slightly dark
Sept 13 - Cancer 3rd 5:59 Dec +15 33 Alt 52.56 Dis 393,922 Dark
By ordinal number:
March
1st 00:36 - middle 390,364 middle -1.45 middle
2nd 20:21 earliest 374,548 closest +17 57 highest
3rd 6:40 latest 400,533 farthest -19 47 lowest Leading Edge Dark
August
1st 3:49 middle 383,419 closest +4 11 middle Leading Edge Slightly Dark
2nd 23:37 earliest 400,262 farthest -19 37 lowest
3rd 5:59 latest 393,922 middle +15 33 highest Leading Edge Dark
The only meaningful correlation is Moon phase. When the leading edge was dark, Marsh measured the time to pass through the frame as greatest (and Moon speed as slowest).
In March this was Capricorn, and in Aug/Sept this was Cancer.
I consider the variations in the estimated elapsed times Marsh is presenting as nothing more than measurement error. When the leading edge of the Moon is unlit Marsh has guessed when the leading edge first enters the frame and the moment it touches the right side of the frame. When the leading edge of the Moon was unlit he should have noted when the trailing (lighted) edge was touching the left side of the frame, and when the trailing edge exited the right side of the frame.
I can’t do that because he doesn’t show this. His Moon images just pop out when he thinks the leading edge has touched the right side of the frame.
It’s been pointed out by many people that what Marsh was really seeing was the apparent motion of the Moon due to the Earth’s rotation. Marsh is assuming that he's seeing the ground speed of the Moon over the surface of the FE, without considering the SE model. In the FE model one assumes the observer is motionless and all motions of the Moon would be proper motions. In the SE model the observer is in motion and the Moon is also in motion. Proper motion and apparent motion have to be sorted out; which isn’t easy.
(Even assuming the FE model, Marsh would still have to take distances and perspective into account, which he didn't. He would also have to assume he could measure a difference in speed with his method.)
This is why I'm convinced the varying times are due to measurement error. The apparent motion of the Moon due to orbital speed - and there is such a difference, as I'll show later - is so negligible over a period of just a few minutes that it would not be measurable with Marsh's method in either the SE or FE model.
Marsh made a fundamental error. He assumed the FE model and never considered the SE model.
Assumption: The observer is not moving.
Conclusion: All motion of the Moon observed is proper motion.
Even though Marsh didn't find what he expected - the Moon "over" the Tropic of Capricorn will always be the fastest - he was still convinced that he was seeing some difference in the speed of the Moon, and he sought out evidence of this with a different method. He used data from the site Time and Date and laboriously made charts of his own.
These two -below- show the times the Moon crossed the local meridian in Indonesia, which Marsh uses as an example of how the Moon would act with the observer on the equator.
He's noting the times that the Moon crossed the local meridian. It's well known that the Moon rises 50 minutes later every day on average; but there is a great deal of variation. Marsh is noting the same variation in meridian crossing; which is valid. He's charting the variation in minutes. He has found a cycle which he highlights in yellow.
He produces a chart, which people have noted looks like a heartbeat on an EKG readout.


What he has found is the anomalistic month - the mean time of the moon's revolution from perigee to perigee again. You can see that his highlighted dates correlate with the apogee dates for 2106. Note that there are 12 cycles. Why would there be 12 cycles on a FE?

https://en.wikipedia.org/wiki/Lunar_month#Anomalistic_month
Marsh has re-discovered the anomalistic month - the mean time of the moon's revolution from perigee to perigee again, being approximately 27.554550 days
The Moon's orbit approximates an ellipse rather than a circle. However, the orientation (as well as the shape) of this orbit is not fixed. In particular, the position of the extreme points (the line of the apsides: perigee and apogee), rotates once (apsidal precession) in about 3,233 days (8.85 years). It takes the Moon longer to return to the same apsis because it has moved ahead during one revolution. This longer period is called the anomalistic month and has an average length of 27.554551 days (27 d 13 h 18 min 33.2 s). The apparent diameter of the Moon varies with this period, so this type has some relevance for the prediction of eclipses (see Saros), whose extent, duration, and appearance (whether total or annular) depend on the exact apparent diameter of the Moon. The apparent diameter of the full moon varies with the full moon cycle, which is the beat period of the synodic and anomalistic month, as well as the period after which the apsides point to the Sun again.
An anomalistic month is longer than a sidereal month because the perigee moves in the same direction as the Moon is orbiting the Earth, one revolution in nine years. Therefore, the Moon takes a little longer to return to perigee than to return to the same star.
The anomalistic month has almost the same period as the synodic month. Marsh mistakenly believes he's found a cycle tied to when the Moon "moves from Cancer to the equator." But this is just a coincidence. The change in the declination (and also altitude) of the Moon is due to the Earth's relation to the inclined orbit of the Moon during a synodic month. The change in the Moon's elapsed time from meridian crossing to next meridian crossing is due to when the Moon is at apogee and perigee in its orbit. They were in this particular relation in 2016, but will slowly move away from this over time.
The elapsed time from lunar meridian crossing to next meridian crossing is least when the Moon is at apogee, and greatest when it is at perigee. An explanation for why this is so highlights the importance of understanding proper and apparent motions.
In Marsh's mind, the decreasing number of minutes from one meridian crossing to the next means that the Moon is traveling faster. It's actually the opposite.
Apogee: The point at which the orbiting body is farthest from the Earth. The "top" of the orbit.
Perigee: Closest.
Orbiting bodies move fastest at perigee and slowest at apogee.
When the Moon is at apogee in its orbit, it is farthest from the Earth; on the left in this illustration. It travels slowest in its orbit at apogee.

This next illustration - below - shows the Earth around the Sun; but imagine it's the Moon around the Earth. The Earth rotates on its axis counterclockwise and the Moon orbits counterclockwise.
When the Moon orbits faster at perigee (on the left in this illustration) it moves more miles in its orbit during one Earth day. The Earth's rotation has to "catch up" more. Therefore it takes more time for the Moon to move through our sky.
When the Moon is moving slower at apogee it travels less distance in its orbit. The Earth's rotation doesn't have to catch up as much. Therefore the Moon takes less time to move through our sky.

At perigee:
Proper motion: Faster
Apparent motion to observer on Earth: Slower
At apogee:
Proper motion: Slower
Apparent motion to observer on Earth: Faster
Last edited:
