Rory
Closed Account
Often described as an old wives' tale, the idea of a connection between the phase of the moon and an increase in birth rates still persists today, including among those who work in childbirth, as exemplified in this article at The Huffington Post:
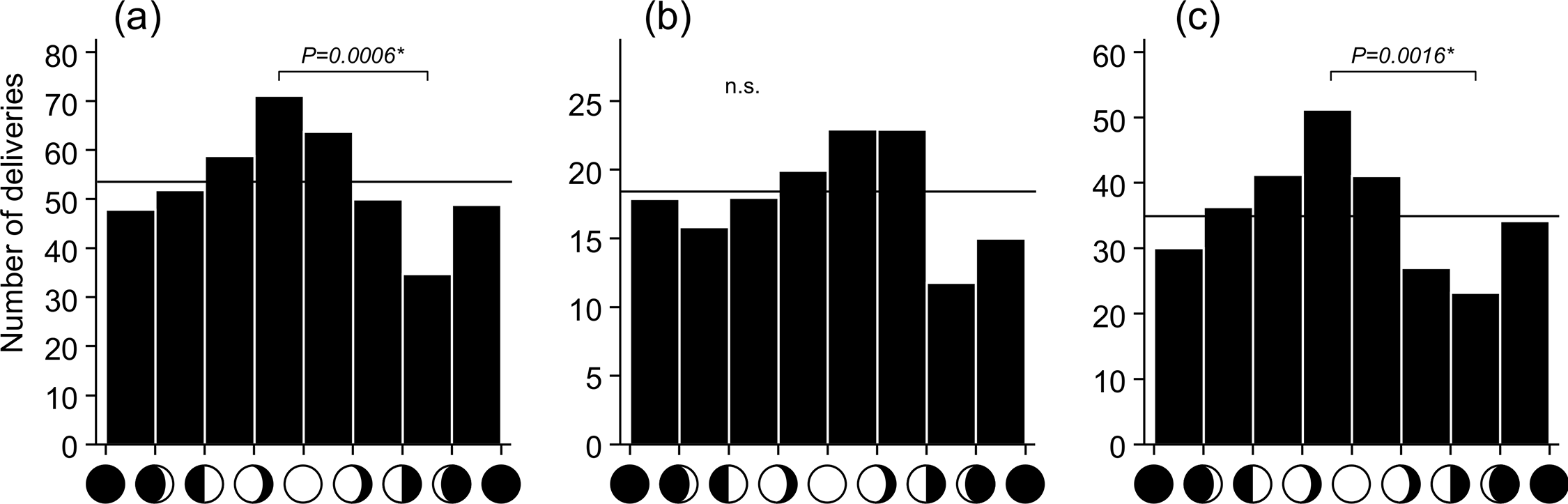
The study using the largest amount of data, however - some 50 millons births - did propose a correlation, concluding that:
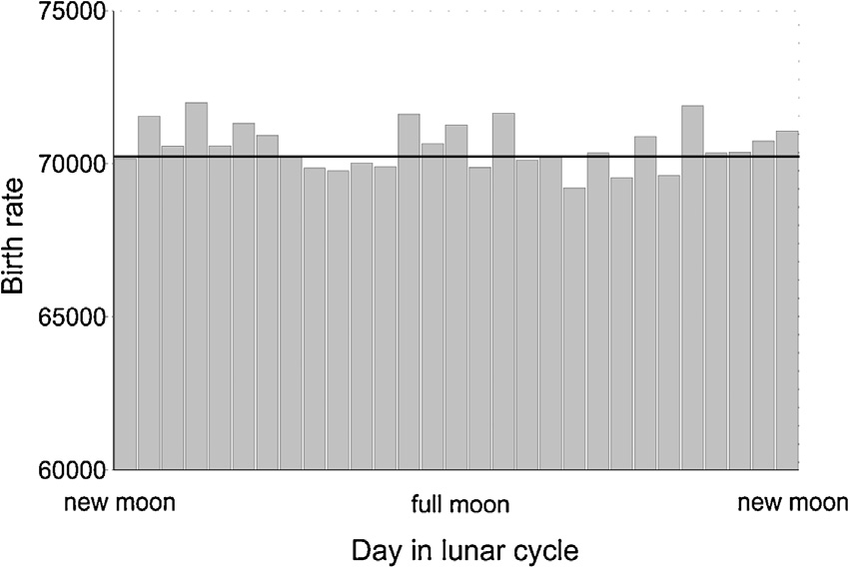
I downloaded 21 years worth of daily birth data, totalling some 89.5 million births, and plotted this against the phase of the moon. While I didn't think it strictly necessary, Caton and Wheatley had performed some data cleansing to eradicate anomalies such as weekends and holidays (substantially lower rates) and Tuesdays (higher rates), so I did this as well (as expected, with such a huge supply of data over a large timescale, it made no significant difference).
These are the results:
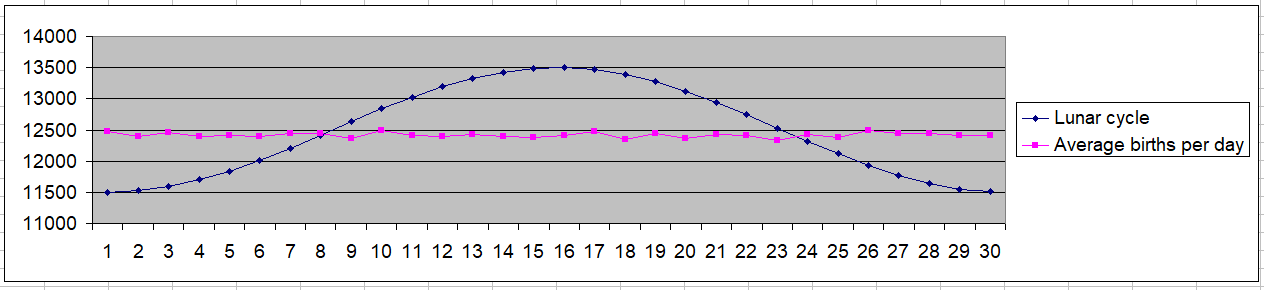
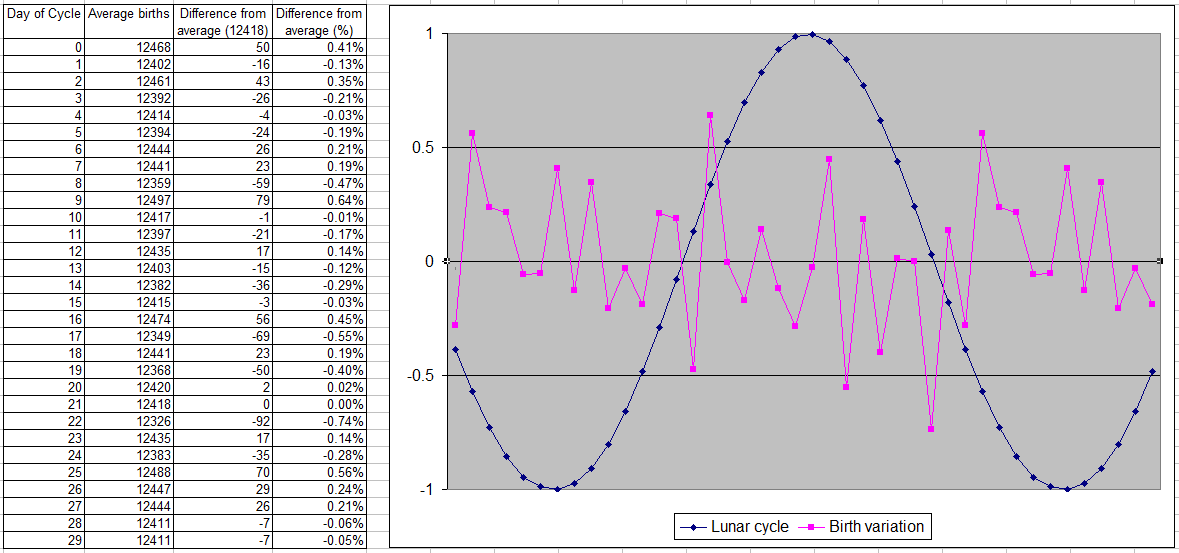
Key: Day 0=new moon; average births per day excluding weekends, holidays and Tuesdays; 13500/+1 in chart=full moon, 11500/-1=new moon; second chart repeats to better represent the lunar cycle
Some conclusions:
If anything further were needed, though, I did find - after completing everything - that Caton and Wheatley had followed up their earlier paper and run an improved model using data for around 70 million births.
This time they found no correlation.
While some early studies appeared to support the idea, later large scale analyses - one looking at over half a million births - found no correlation between birth dates and any particular phase of the moon.An incredible 45 babies entered the world last weekend in Sacramento, California. But some say the mini "baby boom" was no accident. While some doctors joke that the high number of births could be attributed to the full moon, hospital officials hint that the speculation might not be that far out.
"I think if you talk to anybody on the front lines of the hospital, emergency room doctors, labor and delivery, etc. it’s always like that on the full moon, everyone for some reason is really busy," Matthew Guile, a doctor at Sutter Memorial [said].
https://www.huffpost.com/entry/full-moon-babies-lunar-effect_n_927703
The study using the largest amount of data, however - some 50 millons births - did propose a correlation, concluding that:
Despite contradicting other analyses, as well as scientific understanding, given that the source of the study was the Astrophysics Department at Appalachian State University, it seemed worth looking at again. So...Our plots all show a general sinusoidal shape (with a few large deviations), with a peak birthrate around 21 days (third quarter) and a minimum near day 7 (first quarter). The overall shape of the distribution and general agreement with the next largest study [of 5.9 milion births] (Guillon et. al. 1986) suggests that there is indeed a correlation between lunar phase and birthrates. It does not, however, peak at full moon.
Nativity and the Moon: Do Birthrates Depend on the Phase of the Moon? (Caton and Wheatley, I.A.P.P.P., 1998)
I downloaded 21 years worth of daily birth data, totalling some 89.5 million births, and plotted this against the phase of the moon. While I didn't think it strictly necessary, Caton and Wheatley had performed some data cleansing to eradicate anomalies such as weekends and holidays (substantially lower rates) and Tuesdays (higher rates), so I did this as well (as expected, with such a huge supply of data over a large timescale, it made no significant difference).
These are the results:
Key: Day 0=new moon; average births per day excluding weekends, holidays and Tuesdays; 13500/+1 in chart=full moon, 11500/-1=new moon; second chart repeats to better represent the lunar cycle
Some conclusions:
- There is no pattern or correlation with the lunar cycle
- The largest daily variation from average is only 0.74%
- The majority of points lie less than 0.21% from average
- There is no significant increase or decrease in any phase of the moon
- Births on the full moon, and in the three-day period around the full moon, are almost exactly average (-0.03 and +0.14% respectively)
- There are no 'peak' or 'minimum' birth rates, just very slight random variations, as would be expected
If anything further were needed, though, I did find - after completing everything - that Caton and Wheatley had followed up their earlier paper and run an improved model using data for around 70 million births.
This time they found no correlation.
Last edited: