You need the original image. Your example has far more cloud/sky contrast.Blurred clouds with unsharp mask:
If you start out with something like:
You end up with something like
There's quite a few variables though.
You need the original image. Your example has far more cloud/sky contrast.Blurred clouds with unsharp mask:
Make the clouds as dark as they appear in the Gimbal video. There's a very low contrast between the tone of the clouds and the sky, but your example has a very high contrast.
There's quite a few variables though.
Because he hasn't given it much thought, or looked into alternative explanations.So, why is Fravor out there saying there is a "force field" around the Gimbal object?
Because he hasn't given it much thought, or looked into alternative explanations.
If the aura was caused by an unsharp mask process wouldn't/shouldn't Fravor be well familiar with its characteristics or would this sort of minutia be strictly under the purview of the WSO?
Why is that conversation of knots to mph the conversion we should use?Air speed is 241 Knots, 277mph, so in 10 seconds the jet would have travelled 0.77 miles.
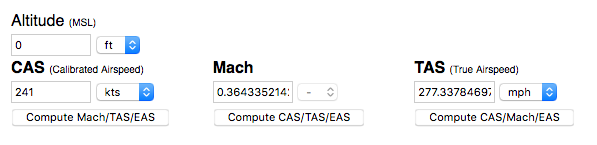
241 knots IS 277 mph, regardless of altitude. There's not question there. It's like converting from mph to km/h At the time I wrote that (Dec 2017) I was unaware that the HUD numbers were CAS not TAS (I only realized that when looking at the Go Fast video later), so I was not converting from CAS to TAS, I was converting from knots to mph. The result is incorrect because I should ALSO have converted from CAS to TAS.Why is that conversation of knots to mph the conversion we should use?
Why is that conversation of knots to mph the conversion we should use?
TAS (True airspeed) is what should be used, regardless of if it's in Knots, mph, fps, kph, or whatever. I'm not arguing with that at all. The problem here is when you say:
No, all I've thought is what I've shown, that CAS --> TAS outputs differ by altitude, and that's true whether it's CAS(knots) --> TAS(mph) or CAS(knots) --> TAS(knots).You seem to think that converting from knots to mph is some kind of conversion that changes with altitude. It's not. It's just multiplying by 1.15078.
403 mph is the correct airspeed to use.So the correct TAS-mph to use in the circumference equation is 403 mph, not 277 mph?
No, all I've thought is what I've shown, that CAS --> TAS outputs differ by altitude, and that's true whether it's CAS(knots) --> TAS(mph) or CAS(knots) --> TAS(knots).
Which looked like you were only discussing Knots -> mphThere seems to be an error in your calculations based on your assuming 241 Knots = 277 mph, which, however, is only true at sea level. At 25,000 ft altitude, 241 Knots = 403 mph (see my last reply above).
There seems to be an error in your calculations based on your assuming 241 Knots = 277 mph, which, however, is only true at sea level. At 25,000 ft altitude, 241 Knots = 403 mph (see my last reply above). Using the sea-level conversion for the Navy jet results in an underestimate of the circumference of the circle it travels, which you give as
((277/60)/60) * (360/1.4) = 19.8 miles
but which should instead be
((403/60)/60) * (360/1.4) = 28.8 miles
That larger circle may place the UFO further away. I'm not trying to be a nitpicking nag, just wanting to nail down exactly what the Navy jet's path was, because we can only know where or if the LOS angles (54˚L and 6˚R) intersect if we know the Navy jet's precise path. And it seems to me that it traveled about 3.4 miles around a circle with a circumference of about 29 miles.
There's another assumption in your above analysis that bugs me, which is: "If we take the target position as essentially fixed..." But what if it was not fixed? That assumption seems to set the UFO's position from the start, yet I want to find out what that position was, if possible. I suspect the best that can be done is to describe a range of possible flight-path scenarios as opposed to one definitive scenario. That the target was essentially fixed may be just one possible scenario.
He seems to think that if the Gimbal was glare it would move smoothly as the heading changes gradually.So this guy on twitter from a relatively new account (April) is claiming the Gimbal video does not show glare as explaining the rotations.
But I do not understand what he is trying to say about the pod movement proving this.
Anyone know what he is talking about?
Just to be clear Mick that's an hypothesis right? We have no conclusive evidence that's how ATFLIR would actually behave in those conditions.He seems to think that if the Gimbal was glare it would move smoothly as the heading changes gradually.
It's an understandable misunderstanding. I really don't discuss that aspect enough.
The sudden movements are from sudden gross movements of the Gimbal as it traverses 0° (and not AT 0°). They are minimized they are noisy. The actual fine tracking is done with internal gimbaled mirrors.
Just to be clear Mick that's an hypothesis right? We have no conclusive evidence that's how ATFLIR would actually behave in those conditions.
For all we know both the ATFLIR and the object might be rotating as we have no way of determining or understanding the actual movements of ATFLIR.
The Navy does have the ability to conclusively prove this obviously with a few tests on an actual ATFLIR of the time.
In any case: the pilots commentary is very precise and gives very clear and direct testimony of the data they had on their screens.
"There's a whole fleet of them look on the SA" (SA = situational awareness screen with data based on radar and data link from AWACS and other aircraft in the area through Data Link used to point ATFLIR)
Lt Graves says the Gimbal video is just part of a longer, higher resolultion video he was shown on the ship. It included several smaller craft, the kind he was more familiar with.
GRAVES: They were essentially flying themselves in a formation. And then behind those was the object you see here.
GRAVES: At this time is pretty much where you see this video, where these are now out of the picture, and it's just this guy that's stationary.
ELIZONDO: Is that why they refer to them as "there's a whole fleet of them"?
GRAVES: Yep. So there wasn't a whole fleet of these, there was just all these little guys. And there's the one object which we had never seen before, which was significantly larger.
- I'm not sure if F-18 has radar contact with the thing (no range indicated, target is not designated). Data on the SA page could come from some "donor" such as AWACS or the fleet radars.
- See also this tutorial on how ATFLIR is guided by the plane radar:
Source: https://www.youtube.com/watch?v=ChsMcv46Rj4
Source: https://twitter.com/uncertainvector/status/1394761778765221889?ref_src=twsrc%5Etfw%7Ctwcamp%5Etweetembed%7Ctwterm%5E1394761778765221889%7Ctwgr%5E%7Ctwcon%5Es1_c10&ref_url=https%3A%2F%2Fwww.redditmedia.com%2Fmediaembed%2Fnfyc3j%3Fresponsive%3Dtrueis_nightmode%3Dtrue
Ryan Graves was not a WSO/Pilot for GIMBAL right, the statements in this thread saying that GIMBAL is from unknown pilots etc are still accurate? Or has there been some new information since?
Also worth noting an update from new knowledge of ATFLIR SLAVE that the ATLFIR in GIMBAL is optically tracking, ie not slaved to L+S (primary radar track) or an other RADAR track.
I don't think so. I believe he knows them, but wont release their namesGraves is making claims on Twitter about this video was he the WSO for the GIMBAL video?
(#467)
It would make sense that he has seen the radar tapes (which are always classified) from the aircraft involved in the encounter, as well as whatever camera footage they shot.Am I correct that he is either involved in operating shipboard radar during the incident, or is speaking for a friend of his who was? Or, at least, that he's speaking about radar observations? Or am I misreading? He seems to be mashing up radar and visual observations, and confusing the issue by not making it clear which is which.
Seeing again this gimbal video, why is the whole image frame jumping slightly at the exact same time as the rotations happen? This indicates to me that: either the camera makes a move at the exact same time the object rotates three times, or the rotation of the object is caused by the gimbal opto-mechanics itself. The latter is of course what I think is happening.
In case this has been discussed already, ignore my comment.
The object is a IR glare and rotates at the point where the camera has to physically rotate due to the gimbal mechanism, the horizon is corrected for by the de-rotation mechanism.
There's probably a reason the Navy called it GIMBAL internally.
I must have watched that gimbal video being picked apart and analyzed a hundred times, and never really picked up on the "bumps". They're incredibly obvious now you've mentioned them.What I mean is that the "bump" of the whole frame is an indicator for it being caused by the optics/glare. Just wanted to point that out..
