LMR
New Member
Surfing the Internet I found an interesting and easy experiment to check Earth rotation. A German scientist invited it in 1940s.
There is a rod (any material), the length is about 1.5 meters and it can freely rotate around a horizontal axis which is in a frame. The frame can rotate around a vertical axis freely.
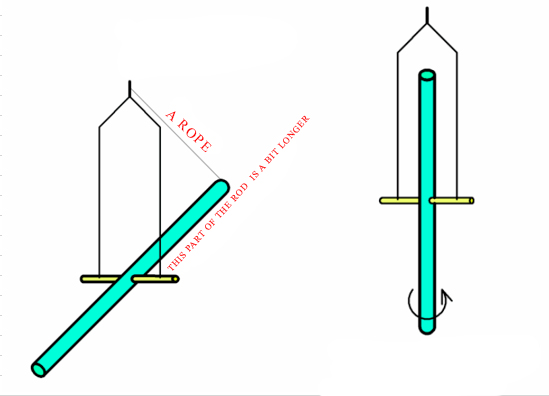
The principle is simple: conservation of angular momentum.
MOI - a moment of inertia
L - angular momentum of the rod
I - a moment of inertia of the rod
w - an angular speed of the rod
L = I * w (by definition)
If the rod (and the frame of course) rotates with Earth, they have angular momentum.
What if we change (decrease) MOI (I) in 10000 times? Well, due to the conservation of angular momentum (L), angular velocity (w) is gonna increase 10000 times.
If w is 0 (Earth does not rotate) it will stay 0. (0 * 10000 = 0)
If w is not 0, it will be 10000 times bigger than 1 rotation per day (2*PI/86146) and the frame will start to rotate counterclockwise (in the Northern hemisphere and clockwise in Southern hemisphere).
The rotation speed of the frame depends on your latitude (the close to a pole, the bigger rotation will be).
No effect on the Equator btw.

The longer a rod is, the better (minimum 1.5 meters). The less radius it has, the better.
Here I put my excel file with calculations and more experiment information (in attachments)
A visual demonstration (external site): link
Right now I live in apartments and I do not have any change to fulfill this experiment. But it is very easy to commit. Well, share your results if you please.
@Mick West what do you think about this experiment? Your opinion is important to me.
Source:
There is a rod (any material), the length is about 1.5 meters and it can freely rotate around a horizontal axis which is in a frame. The frame can rotate around a vertical axis freely.
The principle is simple: conservation of angular momentum.
MOI - a moment of inertia
L - angular momentum of the rod
I - a moment of inertia of the rod
w - an angular speed of the rod
L = I * w (by definition)
If the rod (and the frame of course) rotates with Earth, they have angular momentum.
What if we change (decrease) MOI (I) in 10000 times? Well, due to the conservation of angular momentum (L), angular velocity (w) is gonna increase 10000 times.
If w is 0 (Earth does not rotate) it will stay 0. (0 * 10000 = 0)
If w is not 0, it will be 10000 times bigger than 1 rotation per day (2*PI/86146) and the frame will start to rotate counterclockwise (in the Northern hemisphere and clockwise in Southern hemisphere).
The rotation speed of the frame depends on your latitude (the close to a pole, the bigger rotation will be).
No effect on the Equator btw.
The longer a rod is, the better (minimum 1.5 meters). The less radius it has, the better.
Here I put my excel file with calculations and more experiment information (in attachments)
A visual demonstration (external site): link
Right now I live in apartments and I do not have any change to fulfill this experiment. But it is very easy to commit. Well, share your results if you please.
@Mick West what do you think about this experiment? Your opinion is important to me.
Source:
- Book link Schiller, Motion Mountain, page 145.
- H. Bucka, Zwei einfache Vorlesungsversuche zum Nachweis der Erddrehung, Zeitschrift für Physik 126, pp. 98–105, 1949, and H. Bucka, Zwei einfache Vorlesungsversuche zum Nachweis der Erddrehung. II. Teil, Zeitschrift für Physik 128, pp. 104–107, 1950
Attachments
Last edited:
