Rory
Closed Account
I've been working on a calculator that outputs the predicted visible amount of a distant landmark when there's an obstruction above the horizon, such as a view over terrain with a ridge or intervening mountain. It seems to be working pretty well, and I'd say it's just about finished, but I have one more modification I'd like to make.
First of all, here's the diagram of what it's calculating:
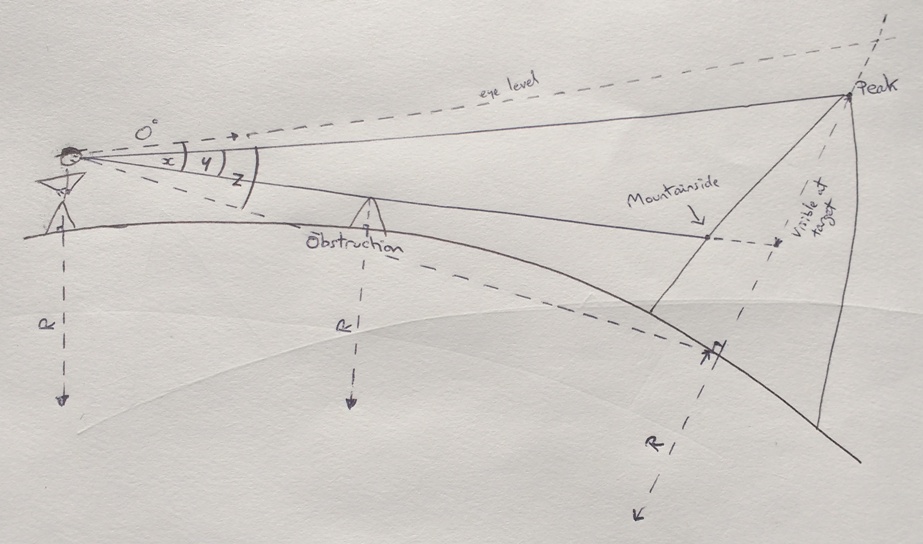
I've gone about it three different ways, firstly two using the drop below eye level - one factoring in for tilt, one more simple without - and then another using angular size, and they all return more or less the same results (for example, for the recent Pikes Peak shot: 1760, 1765, and 1761 feet respectively).
One sticking point I had was that I needed different equations for whether a target was above or below eye level, but the angular size method seems to have dealt with that, and so that's the one I'll probably go with.
Last thing I want to do, though, is take into account where the line of sight actually 'hits' a mountain. For the San Jacinto pictures, for example, while the peak was 122.6 miles away, the part of the mountain seen at the bottom of the visible portion was around 117 miles away. I believe this makes a difference to what the predicted value should be.
It doesn't seem terribly difficult to do this, but I seem to have got myself stuck, and figured the quickest way out of this would be to post this here and see what y'all say.
The latest version of the calculator is attached. First tab is for San Jacinto (simplified drop trig only); second tab is for Pikes Peak (both drop trigs); and third tab is using angular size, with the 'mountainside' equations missing.
Hope that all makes sense.
First of all, here's the diagram of what it's calculating:
I've gone about it three different ways, firstly two using the drop below eye level - one factoring in for tilt, one more simple without - and then another using angular size, and they all return more or less the same results (for example, for the recent Pikes Peak shot: 1760, 1765, and 1761 feet respectively).
One sticking point I had was that I needed different equations for whether a target was above or below eye level, but the angular size method seems to have dealt with that, and so that's the one I'll probably go with.
Last thing I want to do, though, is take into account where the line of sight actually 'hits' a mountain. For the San Jacinto pictures, for example, while the peak was 122.6 miles away, the part of the mountain seen at the bottom of the visible portion was around 117 miles away. I believe this makes a difference to what the predicted value should be.
It doesn't seem terribly difficult to do this, but I seem to have got myself stuck, and figured the quickest way out of this would be to post this here and see what y'all say.
The latest version of the calculator is attached. First tab is for San Jacinto (simplified drop trig only); second tab is for Pikes Peak (both drop trigs); and third tab is using angular size, with the 'mountainside' equations missing.
Hope that all makes sense.
