Rory
Closed Account
Please find attached an excel spreadsheet containing a calculator which works out the viewing (elevation) angles for an observer of a given height on both a flat and sphere earth, from distances and elevations.
This is what it looks like:
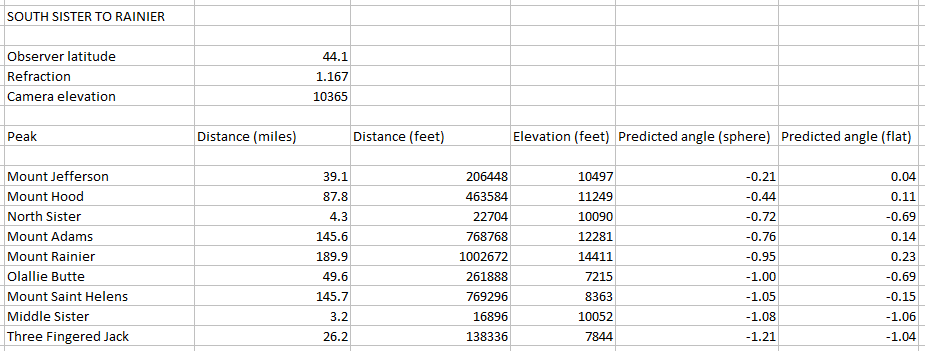
For the flat earth, it's simple trig - tan(x)=(target height-observer height)/distance - while for the sphere earth, it works by calculating a series of isosceles triangles:
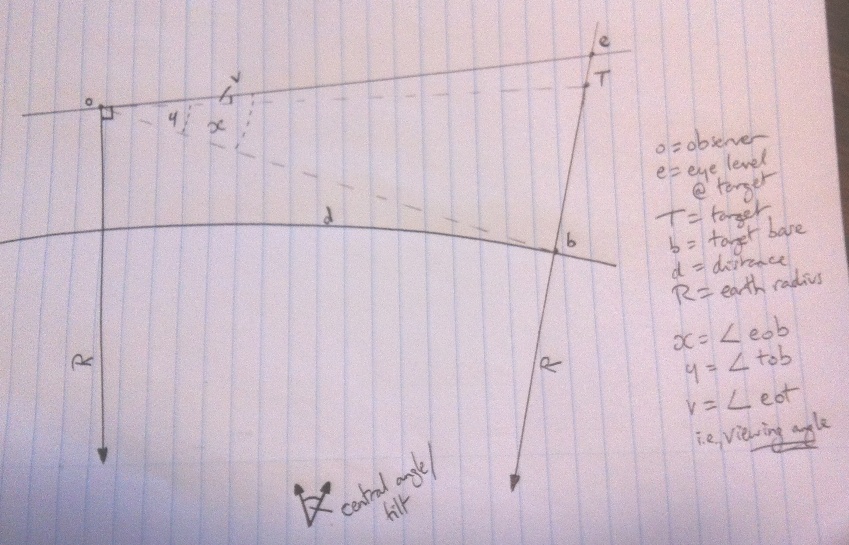
I had done this is in a more straightforward way in the past - but like my obstruction calculator, I found that there was an issue in what happens when targets are above or below eye level (i.e., positive and negative angles).
Now it calculates using angular size, which gets around this problem. Basically: angular size of target - angular size of target base to eye level = viewing/elevation angle.
I've checked it against three other methods of calculating the viewing angle, and they all come to the same result (within ~5/1000th of a degree).
This can then be used to check apparent height order in photographs, and even to predict at what approximate pixel height a landmark should appear.
Here is where it predicts the mountains listed above should appear on a sphere earth:

And here's where it predicts they should appear on a flat earth:

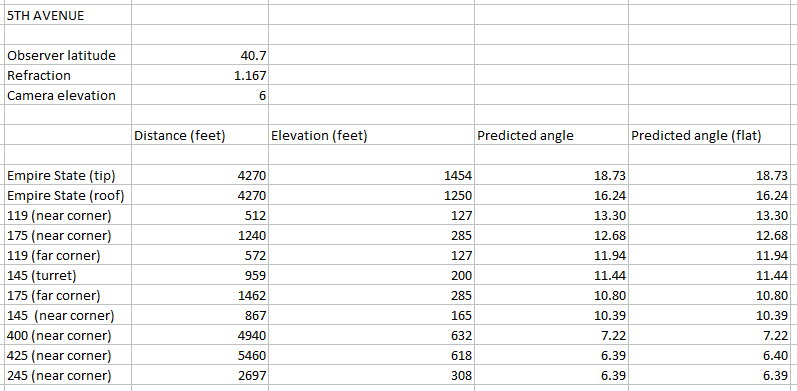
I've also tested it over short range, using a photograph of 5th Avenue in New York (more discussion of this here):

This time, because of the smaller distances, both models return the same results:
The predicted pixel heights for this photo were incredibly accurate, given the rough and ready nature of the method:
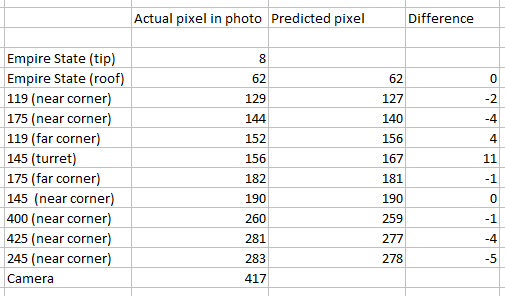
This is based on calculating the number of pixels per degree by choosing the highest and lowest landmarks - in this case, the lowest would be the camera, discerned by parallel lines - and then multiplying the generated angles by that number.
Greater accuracy may be obtained by using different landmarks for this figure, or by factoring in the slight incline of 5th Avenue (it's about 20 feet higher near the Empire State than at 17th Street, where the camera was) - but, given that most of them are within 4 pixels, I think it's a pretty satisfying result.
This is what it looks like:
For the flat earth, it's simple trig - tan(x)=(target height-observer height)/distance - while for the sphere earth, it works by calculating a series of isosceles triangles:
I had done this is in a more straightforward way in the past - but like my obstruction calculator, I found that there was an issue in what happens when targets are above or below eye level (i.e., positive and negative angles).
Now it calculates using angular size, which gets around this problem. Basically: angular size of target - angular size of target base to eye level = viewing/elevation angle.
I've checked it against three other methods of calculating the viewing angle, and they all come to the same result (within ~5/1000th of a degree).
This can then be used to check apparent height order in photographs, and even to predict at what approximate pixel height a landmark should appear.
Here is where it predicts the mountains listed above should appear on a sphere earth:
And here's where it predicts they should appear on a flat earth:
I've also tested it over short range, using a photograph of 5th Avenue in New York (more discussion of this here):
This time, because of the smaller distances, both models return the same results:
The predicted pixel heights for this photo were incredibly accurate, given the rough and ready nature of the method:
This is based on calculating the number of pixels per degree by choosing the highest and lowest landmarks - in this case, the lowest would be the camera, discerned by parallel lines - and then multiplying the generated angles by that number.
Greater accuracy may be obtained by using different landmarks for this figure, or by factoring in the slight incline of 5th Avenue (it's about 20 feet higher near the Empire State than at 17th Street, where the camera was) - but, given that most of them are within 4 pixels, I think it's a pretty satisfying result.
Attachments
Last edited:
