Bunkmeister
New Member
In discussing horizons and visibility with flat earthers, a US Coast Guard geographic range table was brought to my attention. This is a guide for estimating visibility distances over open water.
The full document that this came from here is here on page 7 (https://www.navcen.uscg.gov/pdf/lightLists/LightList V6.pdf) but I have attached the relevant portion below.
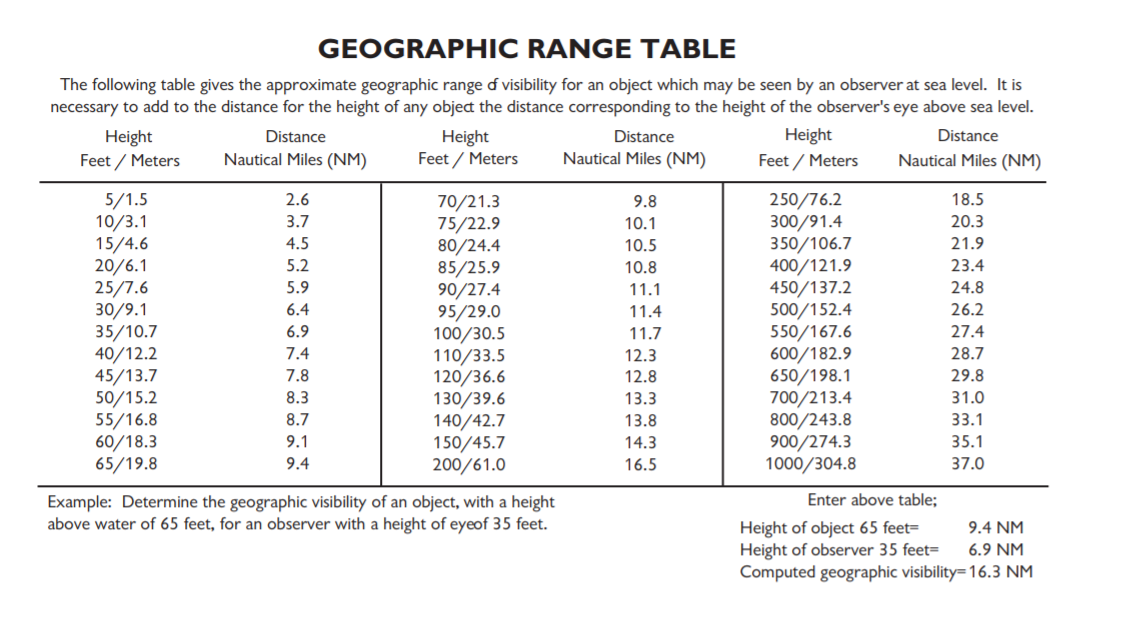
As I read this, one takes the provided nautical miles distance of the observer height and the object height, adds them together, and can get a quick estimate of visibility range.
In the sample example provided above, the observer height is 35 feet, object height is 65 feet, and the computed geographic visibility is 16.3 nautical miles (18.76 regular miles). I plugged in 18.76 miles to the curve calculator, and 88 feet is the amount hidden, a full 23 feet more than the purported object. Does this not contradict generally accepted notions of curvature? Am I missing something?
The full document that this came from here is here on page 7 (https://www.navcen.uscg.gov/pdf/lightLists/LightList V6.pdf) but I have attached the relevant portion below.
As I read this, one takes the provided nautical miles distance of the observer height and the object height, adds them together, and can get a quick estimate of visibility range.
In the sample example provided above, the observer height is 35 feet, object height is 65 feet, and the computed geographic visibility is 16.3 nautical miles (18.76 regular miles). I plugged in 18.76 miles to the curve calculator, and 88 feet is the amount hidden, a full 23 feet more than the purported object. Does this not contradict generally accepted notions of curvature? Am I missing something?