Some youtubers claim that celestial navigation is based on elevation angles from a Flat Earth. For example:
There are various ways to check the validity of this claim. One option is to read a book about the subject, and see what kind for formulas are used to do the calculations. A nice resource that I like to use is
Understanding the maths behind all of this is challenging. My idea for this debunk is to use data from multiple screenshots from my Nautical Almanac App (link: https://play.google.com/store/apps/details?id=com.skrypkin.nauticalalmanac) to show that the data from my app contradicts the claim. Using a combination of times and dates and positions that I found, only simple arithmetic operations are needed to do a sanity check on the output of the program.
I will use 2 main premises to analyze the numbers from the app:

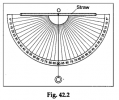
And this is a modified version of the image, which illustrates the type of calculation I will use:

I took 12 screenshots from my Nautical Almanac app. They involve 4 Geographical Positions (GP's):
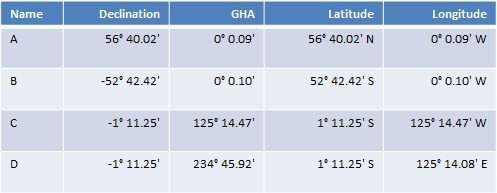
My app won’t show the Latitude of Longitude of the substellar points, but it will show the Greenwich Hour Angle (GHA) and Declination, from which the GP can be derived. The relationship between them two should be obvious from the table. For point D, because the GHA is greater than 180°, the longitude East is calculated by 360° - 234° 45.92' = 125° 14.08'.
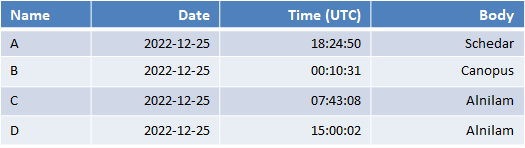
Each of the 4 GP’s is associated with a moment in time when a star is directly above that position:
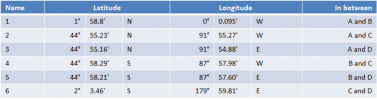
In celestial navigation, it is common to calculate the Height (=elevation angle) and Azimuth of a star from a certain Assumed Position and time. I have chosen positions halfway in between each combination of GP’s:
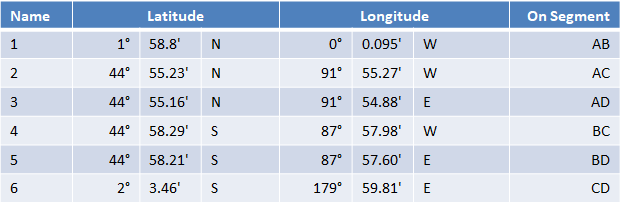
Using Assumed Position 1 and the times for A (left) and B (right):
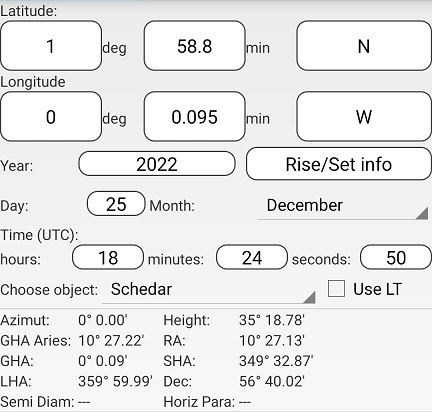
The difference in azimuths is 180° - 0° = 180°.
The distance to both A and B is (90° - 35° 18.78') x 60 = 3281.22 nm
This gives AB = 3281.22 + 3281.22 = 6562.44 nm
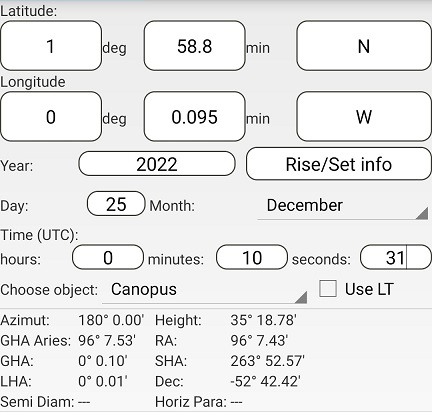
Using Assumed Position 2 and the times for A (left) and C (right):

The difference in azimuths is 222° 15.06' – 42° 15.06' = 180°
The distance to both A and C is (90° - 35° 14.08') x 60 = 3285.92 nm
This gives AC = 3285.92 + 3285.92 = 6571.84 nm
Using Assumed Position 3 and the times for A (left) and D (right):


The difference in azimuths is 317° 44.90' – 137° 44.90' = 180°
The distance to both A and D is (90° - 35° 14.13’) x 60 = 3285.87 nm
This gives AD = 3285.87 + 3285.87 = 6571.74 nm
Using Assumed Position 4 and the times for B (left) and C (right):
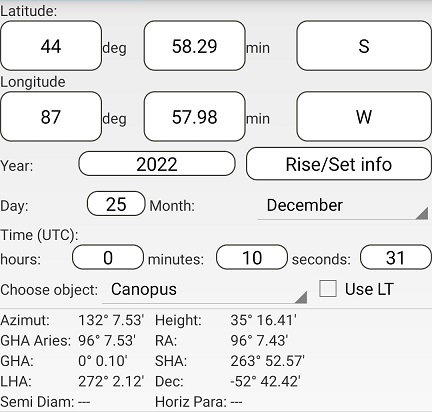
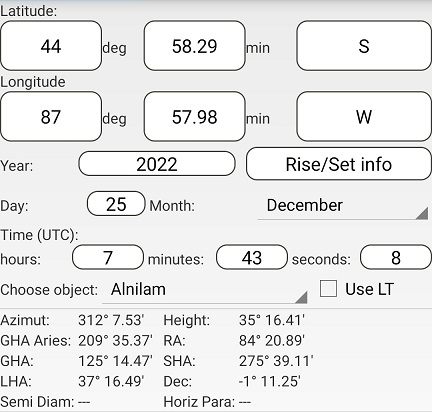
The difference in azimuths is 312° 7.53' – 132° 7.53' = 180°
The distance to both B and C is (90° - 35° 16.41') x 60 = 3283.59 nm
This gives BC = 3283.59 + 3283.59 = 6567.18 nm
Using Assumed Position 5 and the times for B (left) and D (right):
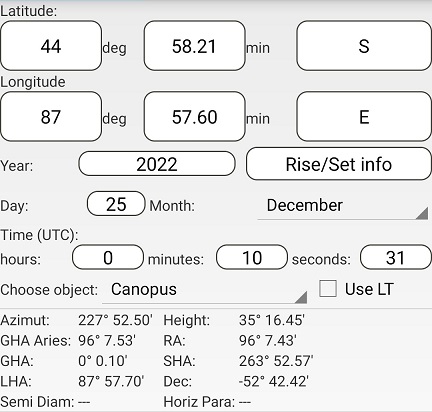
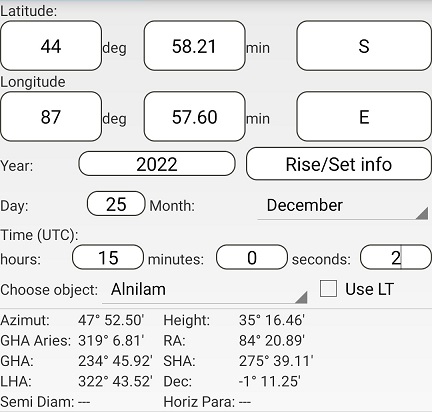
The difference in azimuths is 227° 52.50' – 47° 52.50' = 180°
The distance to B is (90° - 35° 16.45') x 60 = 3283.55 nm
The distance to D is (90° - 35° 16.46') x 60 = 3283.54 nm
This gives BD = 3283.55 + 3283.54 = 6567.09 nm
Using Assumed Position 6 and the times for C and D:
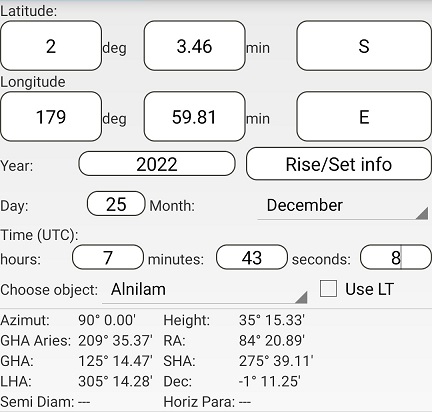
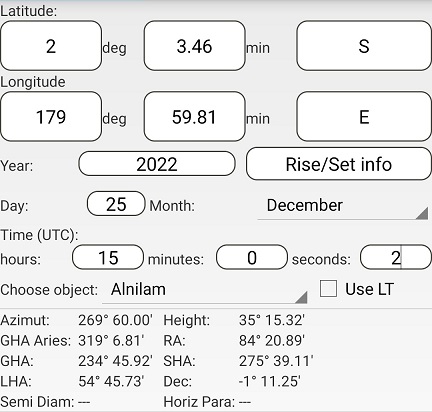
The difference in azimuths is 270° - 90° = 180°
The distance to C is (90° - 35° 15.33') x 60 = 3284.67 nm
The distance to D is (90° - 35° 15.32') x 60 = 3284.68 nm
This gives CD = 3284.67 + 3284.68 = 6569.35 nm
In summary, we found the following distances:
AB = 6562
AC = 6572
AD = 6572
BC = 6567
BD = 6567
CD = 6569
If we try to make a map of the flat earth that this is supposedly based on, with accurate distances, once we have placed A, B and C on it, we can’t find a place for point D such that the distances to the other 3 points are correct:
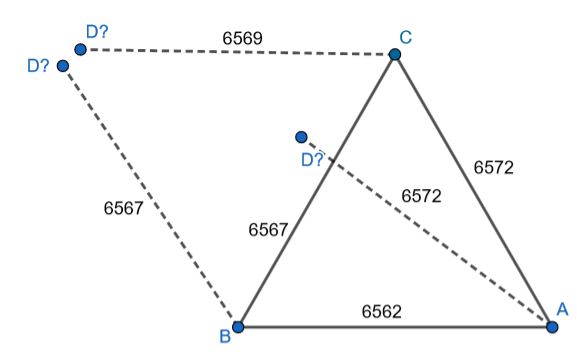
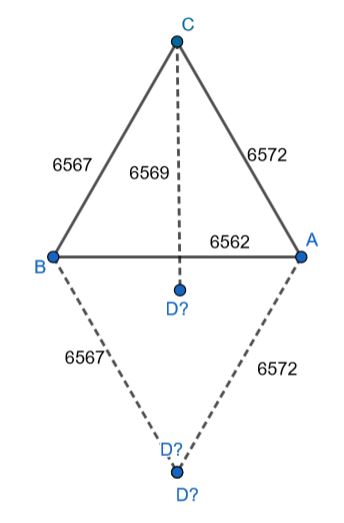

The 6 distances between these 4 points, being impossible on a flat surface, contradict the claim that a Flat Earth is being used as the basis for celestial navigation.
Not only is celestial navigation allegedly based on a Flat Earth, it works so well that it amounts to proof that the earth is flat!
There are various ways to check the validity of this claim. One option is to read a book about the subject, and see what kind for formulas are used to do the calculations. A nice resource that I like to use is
The website hosts many PDF files with formulas and explanations.
Understanding the maths behind all of this is challenging. My idea for this debunk is to use data from multiple screenshots from my Nautical Almanac App (link: https://play.google.com/store/apps/details?id=com.skrypkin.nauticalalmanac) to show that the data from my app contradicts the claim. Using a combination of times and dates and positions that I found, only simple arithmetic operations are needed to do a sanity check on the output of the program.
I will use 2 main premises to analyze the numbers from the app:
- The distance to a Geographical Position (GP) is the Zenith Distance multiplied by 60 nm. The zenith distance will be calculated as 90° – Height. Note that ‘Height’ means ‘Elevation angle’ in this context.
- If the difference in Azimuths is 180° then the distance between 2 GP’s can be calculated by adding the two distances. This is trivial, and follows from the Law of Cosines.
And this is a modified version of the image, which illustrates the type of calculation I will use:
I took 12 screenshots from my Nautical Almanac app. They involve 4 Geographical Positions (GP's):
My app won’t show the Latitude of Longitude of the substellar points, but it will show the Greenwich Hour Angle (GHA) and Declination, from which the GP can be derived. The relationship between them two should be obvious from the table. For point D, because the GHA is greater than 180°, the longitude East is calculated by 360° - 234° 45.92' = 125° 14.08'.
Each of the 4 GP’s is associated with a moment in time when a star is directly above that position:
In celestial navigation, it is common to calculate the Height (=elevation angle) and Azimuth of a star from a certain Assumed Position and time. I have chosen positions halfway in between each combination of GP’s:
Using Assumed Position 1 and the times for A (left) and B (right):
The difference in azimuths is 180° - 0° = 180°.
The distance to both A and B is (90° - 35° 18.78') x 60 = 3281.22 nm
This gives AB = 3281.22 + 3281.22 = 6562.44 nm
Using Assumed Position 2 and the times for A (left) and C (right):
The difference in azimuths is 222° 15.06' – 42° 15.06' = 180°
The distance to both A and C is (90° - 35° 14.08') x 60 = 3285.92 nm
This gives AC = 3285.92 + 3285.92 = 6571.84 nm
Using Assumed Position 3 and the times for A (left) and D (right):
The difference in azimuths is 317° 44.90' – 137° 44.90' = 180°
The distance to both A and D is (90° - 35° 14.13’) x 60 = 3285.87 nm
This gives AD = 3285.87 + 3285.87 = 6571.74 nm
Using Assumed Position 4 and the times for B (left) and C (right):
The difference in azimuths is 312° 7.53' – 132° 7.53' = 180°
The distance to both B and C is (90° - 35° 16.41') x 60 = 3283.59 nm
This gives BC = 3283.59 + 3283.59 = 6567.18 nm
Using Assumed Position 5 and the times for B (left) and D (right):
The difference in azimuths is 227° 52.50' – 47° 52.50' = 180°
The distance to B is (90° - 35° 16.45') x 60 = 3283.55 nm
The distance to D is (90° - 35° 16.46') x 60 = 3283.54 nm
This gives BD = 3283.55 + 3283.54 = 6567.09 nm
Using Assumed Position 6 and the times for C and D:
The difference in azimuths is 270° - 90° = 180°
The distance to C is (90° - 35° 15.33') x 60 = 3284.67 nm
The distance to D is (90° - 35° 15.32') x 60 = 3284.68 nm
This gives CD = 3284.67 + 3284.68 = 6569.35 nm
In summary, we found the following distances:
AB = 6562
AC = 6572
AD = 6572
BC = 6567
BD = 6567
CD = 6569
If we try to make a map of the flat earth that this is supposedly based on, with accurate distances, once we have placed A, B and C on it, we can’t find a place for point D such that the distances to the other 3 points are correct:
The 6 distances between these 4 points, being impossible on a flat surface, contradict the claim that a Flat Earth is being used as the basis for celestial navigation.