There are two issues with the Gimbal simulation, which I think I've now resolved.
1 - The difference between the cloud horizon and the artificial horizon over the first 22 seconds
2 - The possible slight apparent continuous clockwise rotation of the object over the first 22 seconds
Both these issues only affect the first 22 seconds and not a lot. They don't make any difference to the four observable that demonstrate we are looking at a rotating glare, except in the sense that it's now both more accurate in terms of the physics and in the end results.
The original Gimbal sim: https://www.metabunk.org/gimbal1/
And the latest one https://www.metabunk.org/gimbal/
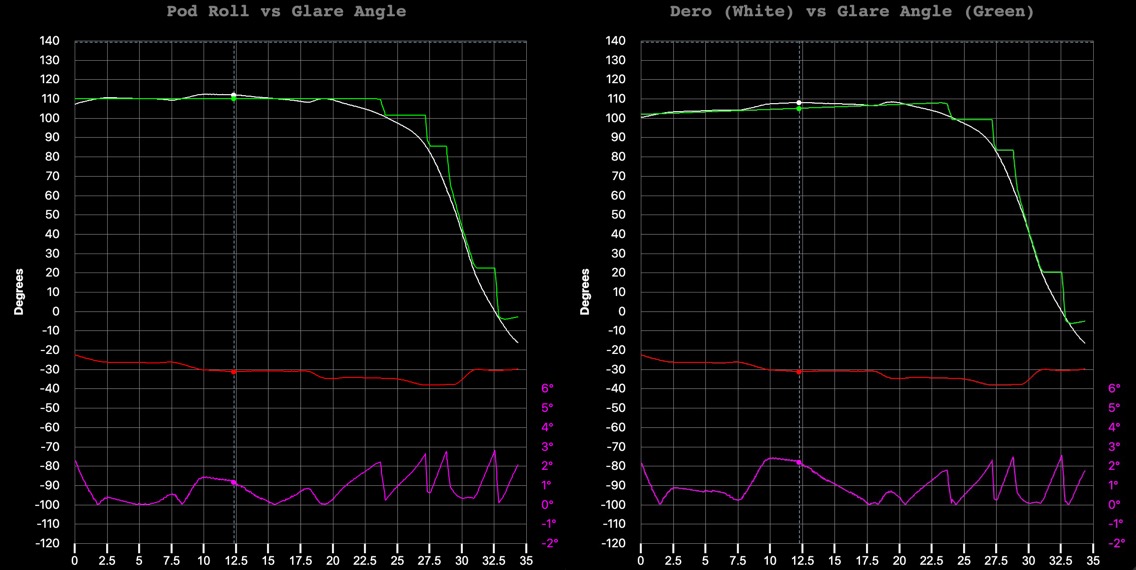
The main differences are illustrated by comparing these graphs (old on the left, new on the right)
And looking at the simulated view, first frame:

The first issue is discussed here:
https://www.metabunk.org/threads/gimbal-derotated-video-using-clouds-as-the-horizon.12552/
The short version is that by measuring the direction the clouds moved in (parallel to the horizon), it was clear that this was at a shallower angle than the artificial horizon, most so when looking left.
The reason for this is that the horizon angle in the ATFLIR image should match what the pilot sees when they look in the same direction. I was previously assuming the horizon angle would be the same as the jet's bank angle (i.e. the same as the artificial horizon). But that's only true when looking forward. When looking more to the side then the bank angle contribution is diminished, and you get some more of the pitch angle. The precise math for calculating the desired horizon angle is found here: https://www.metabunk.org/threads/gi...using-clouds-as-the-horizon.12552/post-276183 and explained:
This was easy to implement in Sitrec (not uploaded yet), but the Gimbal Simulator was more complicated. The problem being that the horizon angle (previously the bank angle) is used to calculate the derotation amount, which is equal to the glare angle. This relationship was used in reverse so that the glare angle could drive the pod's rotation (one line of code), and hence necessary derotation, and then it was shown this created a stepped curve (the green curve in the charts above) that closely followed the ideal derotation (the white curve). You see in the chart, it's labeled "pod roll vs. glare angle" since pod roll = deroation.
But with the more accurate and complicated calculation of the desired horizon, there was now the problem of how you go from glare angle to pod roll. Glare angle is still equal to derotation, so you can phrase it as how to find the pod roll for a given derotation.
Essentially what I do is first calculate the pod pitch and roll for the ideal track (the white curve) and then keep everything else constant and do a binary search, varying pod roll, until I get the desired derotation. This new pod roll then physically drives the pod head. In the sim the green dot indicates where the pod head is physically looking. The white dot indicates the actual target, which needs to stay withing 5° of the green dot so that the additional mirrors can keep it centered.
Doing this adjustment gives this graph. The magenta is a magnified measure of the angle between the green and white dots (not the graphed lines, which are dero). It stays under 5°, but it has got worse.
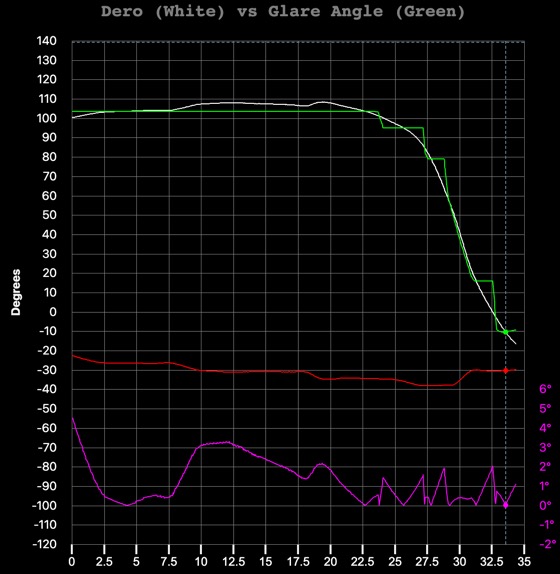
This is where the second issue comes in. Many people have argued that the gimbal shape has a slight clockwise rotation over the first 22 seconds. This is hard to measure due to the switching from WHT to BLK, but a good case has been made that it's there. I've not worried too much about it as it does not make a huge difference, but on reviewing it I think it's quite plausible. Incorporating a slight clockwise rotation ends up removing the increased error. The actual amount is not that important, anything from 3° to 16° keeps the error under 4°, but I picked 6°. You can play with this value at "Glare Initial Rotation" under Tweaks.
This was all rather complicated. It's probable that there's an analytical solution to finding roll from dero. But the numerical solution (binary search) is robust, being accurate essentially by definition.
Here's the code for that bit, full new code attached.
And just to reiterate, this does not really change any of the observables. The initial slight continuous rotation does not change the fact when the jet banks, the horizon rotates, but the object does not. And the fourth observable, the derotation matching the glare angle, is still just as accurate as before. The main change is that the simulator now looks even more like the real video in terms of the horizon angle and the slight initial rotation.
1 - The difference between the cloud horizon and the artificial horizon over the first 22 seconds
2 - The possible slight apparent continuous clockwise rotation of the object over the first 22 seconds
Both these issues only affect the first 22 seconds and not a lot. They don't make any difference to the four observable that demonstrate we are looking at a rotating glare, except in the sense that it's now both more accurate in terms of the physics and in the end results.
The original Gimbal sim: https://www.metabunk.org/gimbal1/
And the latest one https://www.metabunk.org/gimbal/
The main differences are illustrated by comparing these graphs (old on the left, new on the right)
And looking at the simulated view, first frame:
The first issue is discussed here:
https://www.metabunk.org/threads/gimbal-derotated-video-using-clouds-as-the-horizon.12552/
The short version is that by measuring the direction the clouds moved in (parallel to the horizon), it was clear that this was at a shallower angle than the artificial horizon, most so when looking left.
The reason for this is that the horizon angle in the ATFLIR image should match what the pilot sees when they look in the same direction. I was previously assuming the horizon angle would be the same as the jet's bank angle (i.e. the same as the artificial horizon). But that's only true when looking forward. When looking more to the side then the bank angle contribution is diminished, and you get some more of the pitch angle. The precise math for calculating the desired horizon angle is found here: https://www.metabunk.org/threads/gi...using-clouds-as-the-horizon.12552/post-276183 and explained:
(Thanks to @logicbear)I'm assuming that it's intuitive for pilots to look left/right, up/down, but not to tilt their head, so I try to recreate what the horizon would look like if you had a camera strapped to the jet that can only rotate left/right in the wing plane, or up/down perpendicular to that. First I find how much I need to rotate the camera along those lines to look directly at the object, then I compute the angle between a vector pointing right in the camera plane, and the real horizon given by a vector that is tangential to the global 'az' viewing angle.
This was easy to implement in Sitrec (not uploaded yet), but the Gimbal Simulator was more complicated. The problem being that the horizon angle (previously the bank angle) is used to calculate the derotation amount, which is equal to the glare angle. This relationship was used in reverse so that the glare angle could drive the pod's rotation (one line of code), and hence necessary derotation, and then it was shown this created a stepped curve (the green curve in the charts above) that closely followed the ideal derotation (the white curve). You see in the chart, it's labeled "pod roll vs. glare angle" since pod roll = deroation.
But with the more accurate and complicated calculation of the desired horizon, there was now the problem of how you go from glare angle to pod roll. Glare angle is still equal to derotation, so you can phrase it as how to find the pod roll for a given derotation.
Essentially what I do is first calculate the pod pitch and roll for the ideal track (the white curve) and then keep everything else constant and do a binary search, varying pod roll, until I get the desired derotation. This new pod roll then physically drives the pod head. In the sim the green dot indicates where the pod head is physically looking. The white dot indicates the actual target, which needs to stay withing 5° of the green dot so that the additional mirrors can keep it centered.
Doing this adjustment gives this graph. The magenta is a magnified measure of the angle between the green and white dots (not the graphed lines, which are dero). It stays under 5°, but it has got worse.
This is where the second issue comes in. Many people have argued that the gimbal shape has a slight clockwise rotation over the first 22 seconds. This is hard to measure due to the switching from WHT to BLK, but a good case has been made that it's there. I've not worried too much about it as it does not make a huge difference, but on reviewing it I think it's quite plausible. Incorporating a slight clockwise rotation ends up removing the increased error. The actual amount is not that important, anything from 3° to 16° keeps the error under 4°, but I picked 6°. You can play with this value at "Glare Initial Rotation" under Tweaks.
This was all rather complicated. It's probable that there's an analytical solution to finding roll from dero. But the numerical solution (binary search) is robust, being accurate essentially by definition.
Here's the code for that bit, full new code attached.
JavaScript:
// given a jet pitch and roll, and the el and az (the ideal, i.e. the white dod)
// find the pod pitch and roll
// THEN modify roll until the dero for that pitch and roll matches the needed dero for the ideal
// this new roll will give us the green dot (i.e. where the pod head is physically pointing)
function getPodRollFromGlareAngleFrame(frame) {
// return getGlareAngleFromFrame(frame);
// This is what we want the horizon to be
const humanHorizon = get_real_horizon_angle_for_frame(frame)
// actual Jet orientation
var jetPitch = jetPitchFromFrame(frame) // this will get scaled pitch
var jetRoll = jetRollFromFrame(frame)
// ideal az and el (white dot)
var az = Frame2Az(frame)
var el = Frame2El(frame);
// start pod Pitch and Roll for ideal az and el
var podPitch, totalRoll;
[podPitch, totalRoll] = EAJP2PR(el, az, jetPitch);
var podRoll = totalRoll - jetRoll
// what we want the dero to be
const targetDero = getGlareAngleFromFrame(frame)
// and hence what we want the pod horizon angle to be
const horizonTarget = targetDero + humanHorizon
// binary search here modifying podRoll until the dero calculates from jetRoll, jetPitch, podRoll and podPitch
// is close to targetDero
var rollA = podRoll - 90;
var rollB = podRoll + 90;
var horizonA = getPodHorizonFromJetAndPod(jetRoll, jetPitch, rollA, podPitch)
var horizonB = getPodHorizonFromJetAndPod(jetRoll, jetPitch, rollB, podPitch)
var maxIterations = 1000
while (rollB - rollA > 0.01 && maxIterations-- > 0) {
var rollMid = (rollA+rollB)/2;
var horizonMid = getPodHorizonFromJetAndPod(jetRoll, jetPitch, rollMid, podPitch)
// is the horiozn from A to B increasing or decreasing, that will affect which way we compare
if (horizonB > horizonA) {
// horizon is increasing from A to B
if (horizonTarget < horizonMid) {
// target is in the lower part, so Mid is the new B
rollB = rollMid; horizonB = horizonMid;
} else {
// target is in the upper part, so Mid is the new A
rollA = rollMid; horizonA = horizonMid;
}
} else {
// horizon is decreasing from A to B
if (horizonTarget < horizonMid) {
if (horizonTarget < horizonMid) {
// target is in the smaller upper part, so Mid is the new A
rollA = rollMid;
horizonA = horizonMid;
} else {
// target is in the larger lower part, so Mid is the new B
rollB = rollMid;
horizonB = horizonMid;
}
}
}
}
return rollA;
}And just to reiterate, this does not really change any of the observables. The initial slight continuous rotation does not change the fact when the jet banks, the horizon rotates, but the object does not. And the fourth observable, the derotation matching the glare angle, is still just as accurate as before. The main change is that the simulator now looks even more like the real video in terms of the horizon angle and the slight initial rotation.
