Does Benford's Law apply to Elections?

[Jeff Semenak]

I've been interested in Mathematics for some time and, this seems to be correct. Can anyone, back-stop me on this?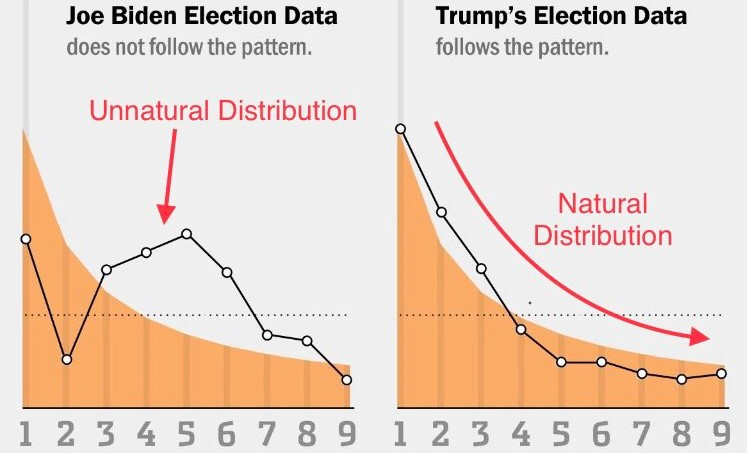

https://gnews.org/534248/

 

[Bdoserror]

The short answer is that Benford's law is being mis-applied here. It's intended for values which have a range of several orders of magnitude. Matt Parker is a mathematics educator on YouTube and explains it here: .

 

[Mendel]

Related.

Source: https://www.youtube.com/watch?v=etx0k1nLn78


Summary: Benford's Law describes the distribution of the first digit of numbers in many real-life data sets, including, sometimes, elections. IN Chicago, Trump's distribution followed this, but Biden's did not. The reason is the size distribution of Precincts is so small and clustered around 500, and even that Benford's law does not apply (as Benford himself explained). Trump got so few votes that they clustered around zero (per precinct), which looked like Benford's law. Biden's just had a normal distribution clustered a bit below 500.

The last two digits are not random because Trump had many results under 100, so a lot of them were two-digits, so that followed the previous distribution.