I have been working off-and-on for a several months on a quantitative comparison between the angle of the glare (which I wrote a script to measure) and the direction of the target, since it is a clear prediction of the glare model that these two should be related, and in a two-axis system, identical up to a constant. In essence, it's just calculating Euler angles, complicated only by the fact that the aircraft is pitching up slightly by some unknown amount (which should change as the bank angle changes and the magnitude of the lift vector has to change to keep altitude constant).
This pitch angle is very important for getting the correct predictions, especially near the sweep-over point. I have seen some in the ufosphere argue that the gimbal object can't be glare because it rotates less than what is "mechanically required" (Lehto mentions this analysis here). The error lies in ignoring the aircraft pitch, since by pitching up it's moving the object away from the gimbal singularity, which reduces the required angle. Unfortunately it's not very easy to estimate since it depends on the aircraft loadout; even if I knew that, I have looked around for tables and charts but most information out there about F-18s and angles of attack pertains to its exceptional performance at high AoAs, which is not what we want, and the manuals only cite angles of attack for landing configurations, which is also not what we want. So we resort to flight simulators. The F-18 flight model in DCS is, I understand, fairly accurate away from the high AoA regime, but the modeled aircraft is the F-18C legacy Hornet, not the F-18E Super Hornet, which is a heavier airplane with a larger wing. MSFS does have a Super Hornet but the flight model is questionable (and I haven't had the chance to try it out anyway since it hit me with a 100 GB+ update). In the interim I'll grab the numbers from DCS which are likely wrong but are the best we got. In the default loadout it gives a pitch-up angle of around 6 or 7 degrees for 250 knots CAS at 25000 feet with a bank angle of roughly 30 degrees.
With this in hand we can do the coordinate transformations to convert the indicate azimuth and elevations into pitch and roll for the ATFLIR pod. This is what you get:
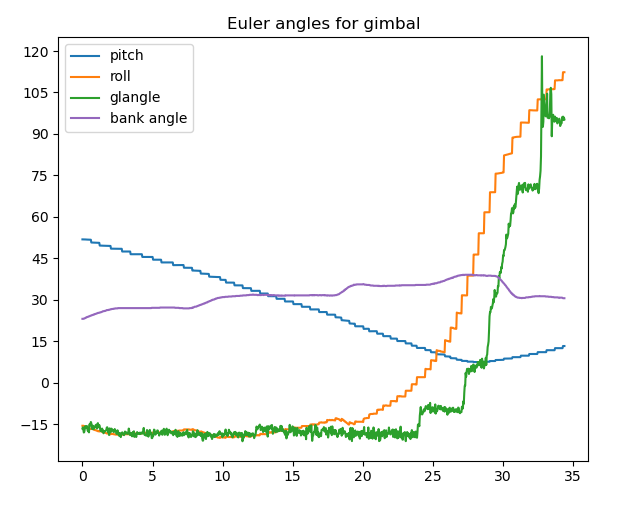
If ATFLIR were a two-axis system, the green and yellow lines should match (the green line, the glare angle, has a somewhat arbitrary zero so I chose it to make this clearer). Circa 16 seconds or so the lines begin to diverge, which I had been worried was an error in my analysis, but the fact that the glare doesn't move at 19 seconds as the airplane banks seems to be the smoking gun that the secondary mirrors are active at this point. You can see this in the graph above as the little dip in the yellow line that has no partner in the green one (note that the yellow and purple lines are on different scales). You'd expect the glare to rotate with the horizon, but it doesn't, because the main roll axis never compensates for the bank. Incidentally, the green line tracks the yellow line very well if you advance it about 1.8 seconds, which seems consistent with some sort of control law for the roll axis.
Still, the difference between the yellow and green lines seems rather large, so it might be questionable whether the secondary mirrors can really make up the difference. To see this, I'll first reconstruct the trajectory that would correspond to the observed glare angle (the pitch is still calculated from the indicated azimuth and elevation), if we had a two-axis system, and then plot it in the moving reference frame of the F-18 as it banks and turns, at a fixed distance to represent the path the object makes in the sky:
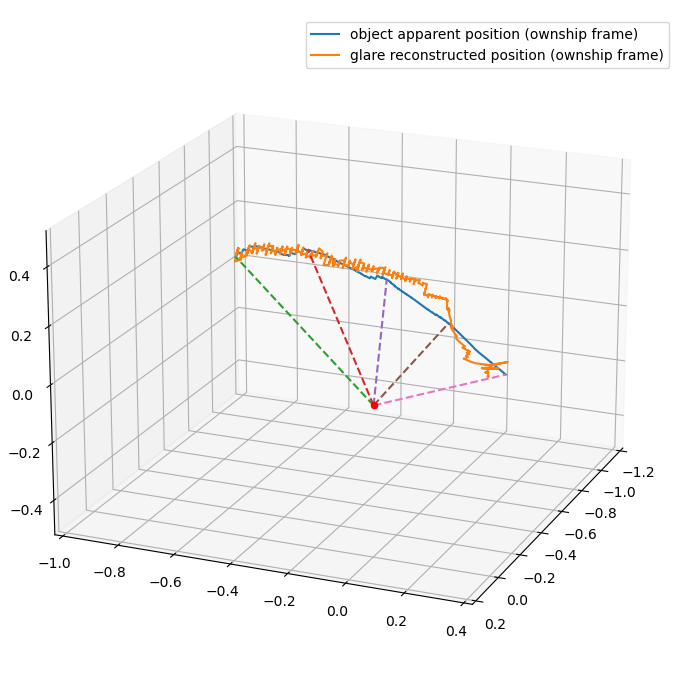
The agreement looks a lot more striking here. Not surprisingly, since the disagreement in rolls would look larger and larger as you approach the gimbal singularity, even for a fixed absolute angular disagreement. Still, is this small enough for the secondary mirrors? The patent mentions
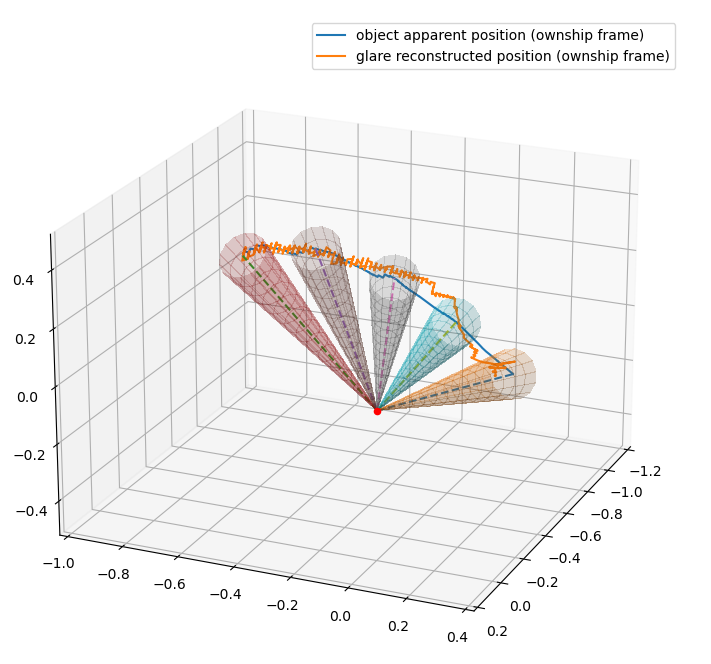
Despite the data limitations, it looks reasonable, and shows clearly that the assertion that the glare "rotates less than what is mechanically required" is incorrect.
Moral: if the point is persuasion, you can probably do worse than @Mendel's pithy point above: real objects rotate with the horizon as the airplane banks. A more detailed explanation is harder.
This pitch angle is very important for getting the correct predictions, especially near the sweep-over point. I have seen some in the ufosphere argue that the gimbal object can't be glare because it rotates less than what is "mechanically required" (Lehto mentions this analysis here). The error lies in ignoring the aircraft pitch, since by pitching up it's moving the object away from the gimbal singularity, which reduces the required angle. Unfortunately it's not very easy to estimate since it depends on the aircraft loadout; even if I knew that, I have looked around for tables and charts but most information out there about F-18s and angles of attack pertains to its exceptional performance at high AoAs, which is not what we want, and the manuals only cite angles of attack for landing configurations, which is also not what we want. So we resort to flight simulators. The F-18 flight model in DCS is, I understand, fairly accurate away from the high AoA regime, but the modeled aircraft is the F-18C legacy Hornet, not the F-18E Super Hornet, which is a heavier airplane with a larger wing. MSFS does have a Super Hornet but the flight model is questionable (and I haven't had the chance to try it out anyway since it hit me with a 100 GB+ update). In the interim I'll grab the numbers from DCS which are likely wrong but are the best we got. In the default loadout it gives a pitch-up angle of around 6 or 7 degrees for 250 knots CAS at 25000 feet with a bank angle of roughly 30 degrees.
With this in hand we can do the coordinate transformations to convert the indicate azimuth and elevations into pitch and roll for the ATFLIR pod. This is what you get:
If ATFLIR were a two-axis system, the green and yellow lines should match (the green line, the glare angle, has a somewhat arbitrary zero so I chose it to make this clearer). Circa 16 seconds or so the lines begin to diverge, which I had been worried was an error in my analysis, but the fact that the glare doesn't move at 19 seconds as the airplane banks seems to be the smoking gun that the secondary mirrors are active at this point. You can see this in the graph above as the little dip in the yellow line that has no partner in the green one (note that the yellow and purple lines are on different scales). You'd expect the glare to rotate with the horizon, but it doesn't, because the main roll axis never compensates for the bank. Incidentally, the green line tracks the yellow line very well if you advance it about 1.8 seconds, which seems consistent with some sort of control law for the roll axis.
Still, the difference between the yellow and green lines seems rather large, so it might be questionable whether the secondary mirrors can really make up the difference. To see this, I'll first reconstruct the trajectory that would correspond to the observed glare angle (the pitch is still calculated from the indicated azimuth and elevation), if we had a two-axis system, and then plot it in the moving reference frame of the F-18 as it banks and turns, at a fixed distance to represent the path the object makes in the sky:
The agreement looks a lot more striking here. Not surprisingly, since the disagreement in rolls would look larger and larger as you approach the gimbal singularity, even for a fixed absolute angular disagreement. Still, is this small enough for the secondary mirrors? The patent mentions
So let's indicate what 5 degrees would look like here:
The third gimbal axis 146 can be of small angular travel (for example, less than or equal to 5 degrees). As a result, the third gimbal axis 146 travels around the roll axis 142 and avoids the gimbal singularity.
Despite the data limitations, it looks reasonable, and shows clearly that the assertion that the glare "rotates less than what is mechanically required" is incorrect.
Moral: if the point is persuasion, you can probably do worse than @Mendel's pithy point above: real objects rotate with the horizon as the airplane banks. A more detailed explanation is harder.
Attachments
Last edited by a moderator:
