Antithesis
New Member
I've been talking to a flat earther who considers sun glitter to be solid evidence for a flat earth.

I've walked him through the explanation: the earth is not curved enough to produce a curved appearance; waves are reflecting the sun toward the viewer, and the angles of the wave normals more than compensate for the angles of the earth normals which point away from the viewer (the earth normal at the horizon is pointed away the most). I've even shown a geometric proof of this.
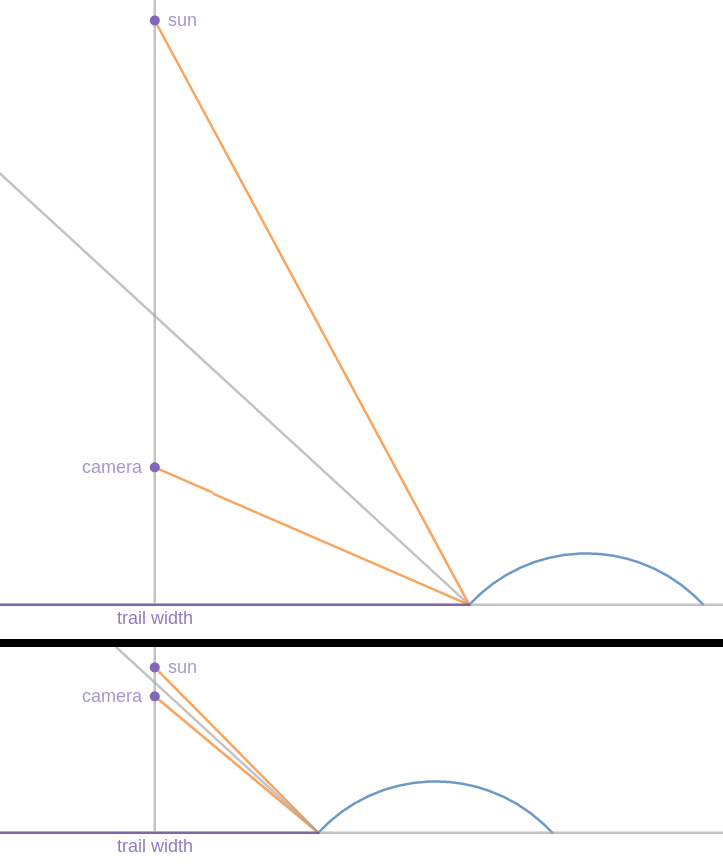
But as is common in flat eartherism, there is a suspicion of mathematics. He wants to see a demonstration. And I have to admit, I'd like to see one too. Specifically, with a physical model we would like to see a spot of specular reflection like this

transform via camera movement into a trail of specular reflection like this

With a little zoom, it might be possible to get the line of sight very close to the surface in order to see something similar to sun glitter.
Does anyone have, or know the location of, a large convex surface covered with tiny bumps?
Diagrams
Two waves reflecting sunlight to the viewer:
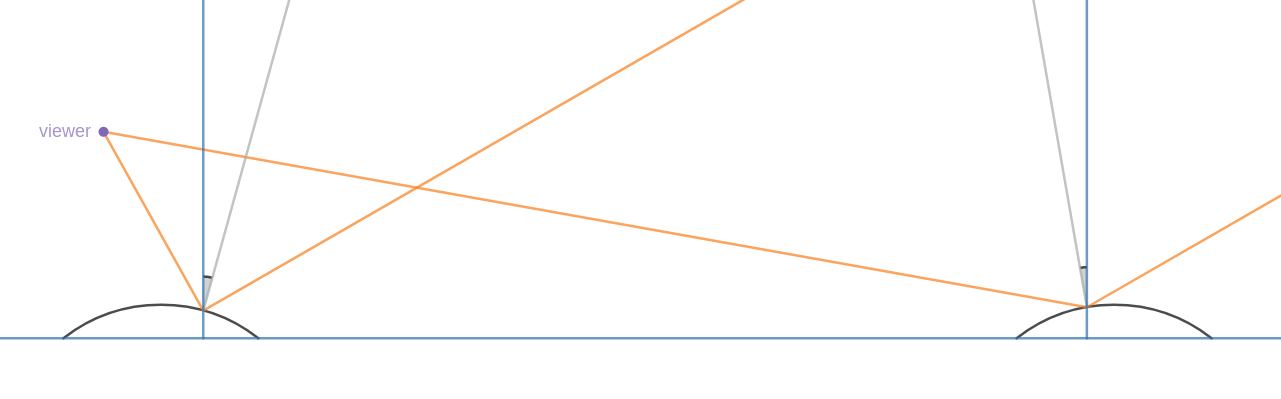
The gray lines are the wave normals. The angles of the wave normals are measured from the earth normals (blue).
A spot-shaped specular reflection is like this:
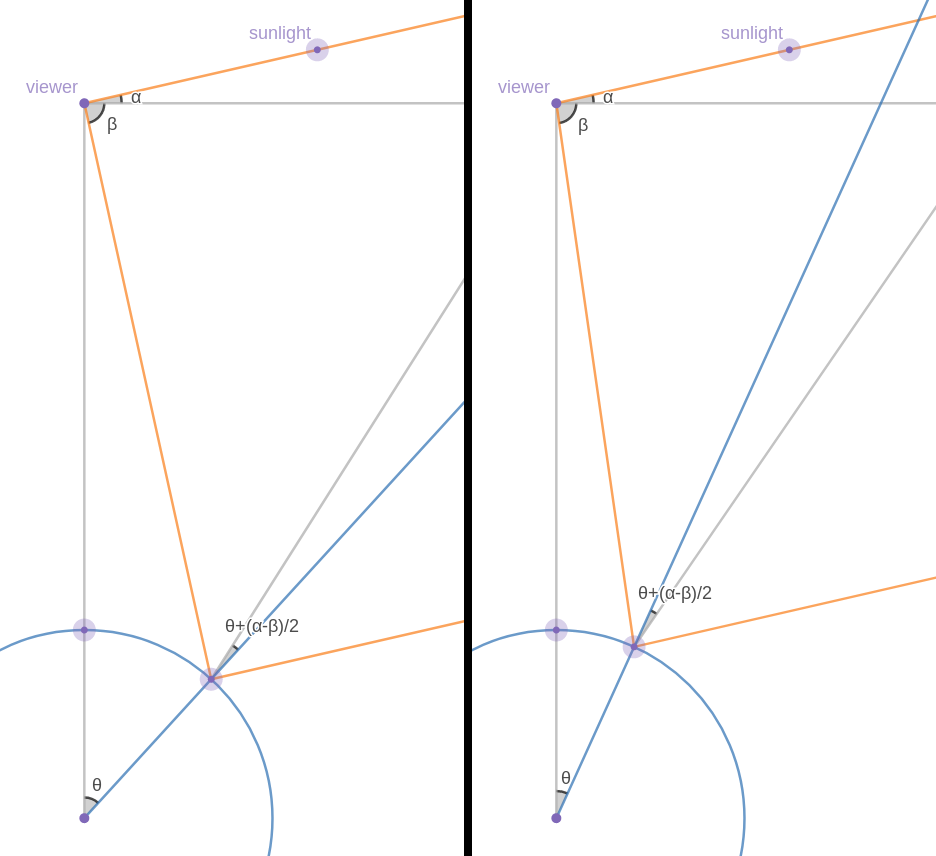
The specular reflection is between those two points. (The derivation θ + (α - β)/2, the angle of the wave normal, is shown later.)
A trail-shaped specular reflection extending to the horizon is like this:
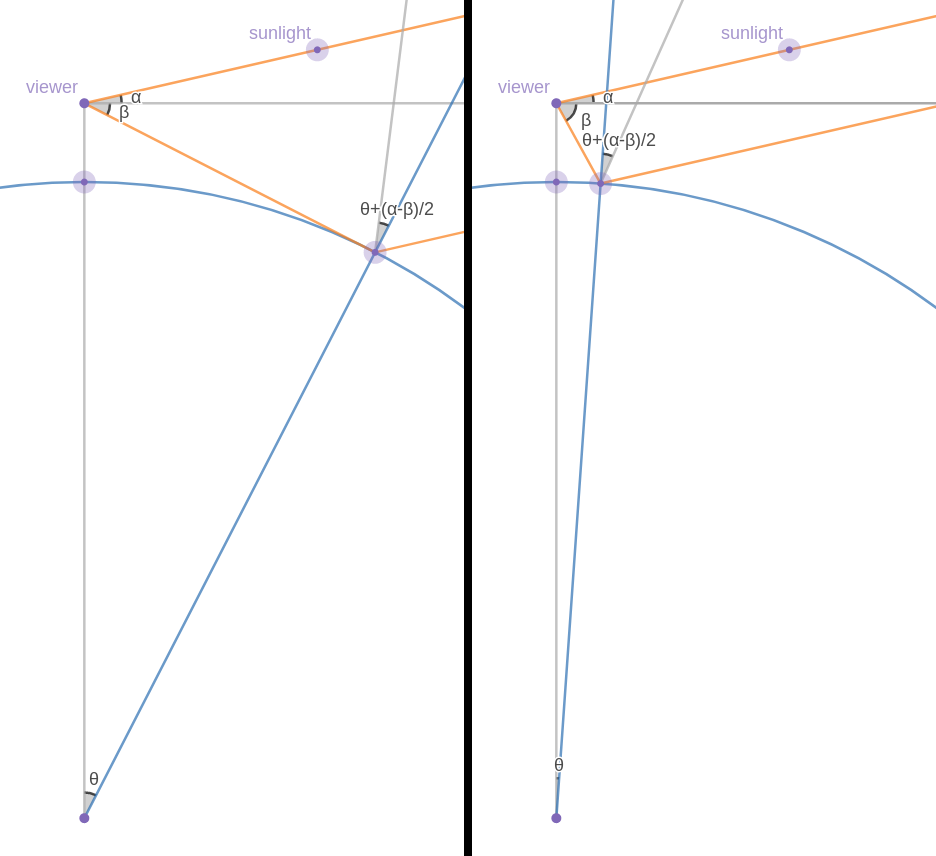
Again, specular reflections are seen everywhere between those two points, hence the trail of sun glitter.
You can move around the purple-haloed points in the live diagram.
Practical calculation
The ideal photo of sun glitter would allow us to estimate the camera height, the angle of the sun, and the distance to the nearest endpoint of the glitter trail. This is good enough:

Since the angular diameter of the sun is about 0.5°, the inclination angle (α) to the top of the sun is roughly 3° (while it is a low flare image of the sun, there is still some flare to ignore).
The farther it is to the start of the glitter trail, the harder it is to prove the glitter extends to the horizon. So let's generously say 50 feet to the glitter. With a viewer height of 6 feet and ignoring the curvature of the earth along 50 feet, β ≈ 6.8° (calculation).
The angle of the wave normal at the start of the glitter is therefore θ + (α - β)/2 ≈ (α - β)/2 ≈ (3 - 6.8)/2 = -1.9°. The negative angle means the wave normal is pointing away from the viewer.
In the last diagram on the left, the dip angle of the horizon β is equal to θ. From a height of 6 feet, β = θ ≈ 0.043° (calculation). The wave normal at the horizon is therefore θ + (α - β)/2 = (α + β)/2 = (3 + 0.043)/2 ≈ 1.52°.
If a wave normal can point 1.9° away from us, then it can certainly point 1.52° toward us. Therefore if the earth is a globe as claimed, then we will see glitter at the horizon.
The last thing to prove is that glitter appears everywhere in between the start of the trail and the horizon. Consider the last diagram again: as we march from the horizon toward the viewer, θ is strictly decreasing and β is strictly increasing. Therefore the angle of the wave normal θ + (α - β)/2 is strictly decreasing, and thus takes on every value in between 1.52° and -1.9°. So at every point along the glitter trail, a wave is able to reflect light to the viewer.
Derivation

β + 2λ + α = 180 (the gray horizontal line through the circle)
(λ - φ) + α + θ = 90 (the angle between the blue earth normal and the gray tangent)
Eliminate λ to obtain φ = θ + (α - β)/2.
Addendum: There is a previous thread on sun glitter, however that concerns the question of why different viewers see their own personal version of sun glitter. That is a different topic, or at least seems sufficiently different from the issue addressed here.

I've walked him through the explanation: the earth is not curved enough to produce a curved appearance; waves are reflecting the sun toward the viewer, and the angles of the wave normals more than compensate for the angles of the earth normals which point away from the viewer (the earth normal at the horizon is pointed away the most). I've even shown a geometric proof of this.
But as is common in flat eartherism, there is a suspicion of mathematics. He wants to see a demonstration. And I have to admit, I'd like to see one too. Specifically, with a physical model we would like to see a spot of specular reflection like this

transform via camera movement into a trail of specular reflection like this

With a little zoom, it might be possible to get the line of sight very close to the surface in order to see something similar to sun glitter.
Does anyone have, or know the location of, a large convex surface covered with tiny bumps?
Diagrams
Two waves reflecting sunlight to the viewer:

The gray lines are the wave normals. The angles of the wave normals are measured from the earth normals (blue).
A spot-shaped specular reflection is like this:

The specular reflection is between those two points. (The derivation θ + (α - β)/2, the angle of the wave normal, is shown later.)
A trail-shaped specular reflection extending to the horizon is like this:

Again, specular reflections are seen everywhere between those two points, hence the trail of sun glitter.
You can move around the purple-haloed points in the live diagram.
Practical calculation
The ideal photo of sun glitter would allow us to estimate the camera height, the angle of the sun, and the distance to the nearest endpoint of the glitter trail. This is good enough:

Since the angular diameter of the sun is about 0.5°, the inclination angle (α) to the top of the sun is roughly 3° (while it is a low flare image of the sun, there is still some flare to ignore).
The farther it is to the start of the glitter trail, the harder it is to prove the glitter extends to the horizon. So let's generously say 50 feet to the glitter. With a viewer height of 6 feet and ignoring the curvature of the earth along 50 feet, β ≈ 6.8° (calculation).
The angle of the wave normal at the start of the glitter is therefore θ + (α - β)/2 ≈ (α - β)/2 ≈ (3 - 6.8)/2 = -1.9°. The negative angle means the wave normal is pointing away from the viewer.
In the last diagram on the left, the dip angle of the horizon β is equal to θ. From a height of 6 feet, β = θ ≈ 0.043° (calculation). The wave normal at the horizon is therefore θ + (α - β)/2 = (α + β)/2 = (3 + 0.043)/2 ≈ 1.52°.
If a wave normal can point 1.9° away from us, then it can certainly point 1.52° toward us. Therefore if the earth is a globe as claimed, then we will see glitter at the horizon.
The last thing to prove is that glitter appears everywhere in between the start of the trail and the horizon. Consider the last diagram again: as we march from the horizon toward the viewer, θ is strictly decreasing and β is strictly increasing. Therefore the angle of the wave normal θ + (α - β)/2 is strictly decreasing, and thus takes on every value in between 1.52° and -1.9°. So at every point along the glitter trail, a wave is able to reflect light to the viewer.
Derivation

β + 2λ + α = 180 (the gray horizontal line through the circle)
(λ - φ) + α + θ = 90 (the angle between the blue earth normal and the gray tangent)
Eliminate λ to obtain φ = θ + (α - β)/2.
Addendum: There is a previous thread on sun glitter, however that concerns the question of why different viewers see their own personal version of sun glitter. That is a different topic, or at least seems sufficiently different from the issue addressed here.
Last edited: