Paul Andrew Smith
New Member
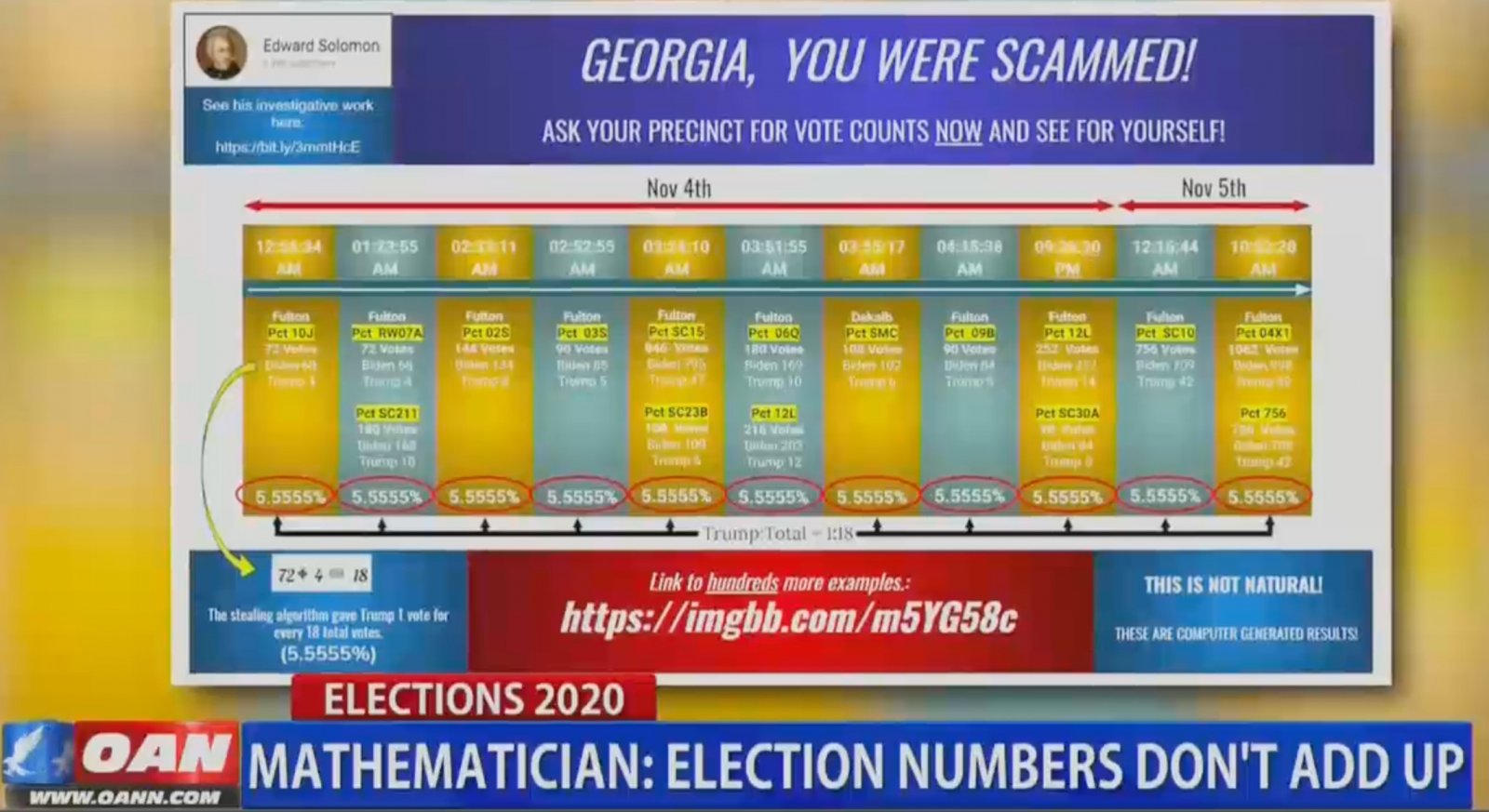
A friend posted this video of Mathematician Edward Solomon seeming to show that Trump won exactly 5.55555556% percent of the votes in multiple different precincts in Georgia during several reporting periods, suggesting that is probabilistically nearly impossible. If true, that does seem to be strange and concerning. Has anyone looked into this to debunk it? I'm at a loss for how to respond. Thanks! https://www.mediamatters.org/one-am...y-theory-computer-programs-changed-votes-2020
[Mod Additions]
The link to "hundreds more examples" goes to the attached image. https://imgbb.com/m5YG58c
The link "See his investigative work here" goes to his YouTube channel: https://www.youtube.com/channel/UCIxc8YMkny2KBaD5TQsSbpg/videos
[Mod Additions]
Article: EDWARD SOLOMON: You could see that there's the first precinct there, it said 12:56 a.m. on November 4. And then when it abandons that ratio on its next tabulation update, two more precincts -- they inherit that ratio on the same time stamp. And then after they update their tabulations and abandoned that ratio of 1:18, another precinct inherits it.
BOBB: Solomon says that in order for the ratios to be that exact at clearly designated times computer software must have used an algorithm to change the votes. Specifically, for roughly 90 minutes at a time for rotating intervals, the precincts changed the votes to ensure that Donald Trump won only 5.555%, after the intervals completed, the precinct's returned to a normal vote count.
SOLOMON: It says that this could only have been done by an algorithm. It can't even be done by humans. So if you had a bunch of human beings that were trying to rig an election, and he said, 'hey, listen, I want you to give Trump 15% over here and I want you to give Trump 13.5% over here, and 5.5% over here,' even human beings trying to replicate this wouldn't get it this perfect.
BOBB: So what are the chances of this happening naturally? Solomon says that there are not enough stars in the universe to which you can compare.
SOLOMON: You can use the binomial probability formula, and the chance of that event happening is 1/10 to an exponent so large there's not enough stars in the universe -- there's not enough atoms in the universe to explain the number. It can't happen naturally.
The link to "hundreds more examples" goes to the attached image. https://imgbb.com/m5YG58c
The link "See his investigative work here" goes to his YouTube channel: https://www.youtube.com/channel/UCIxc8YMkny2KBaD5TQsSbpg/videos
Attachments
Last edited by a moderator:

