R-Squared is a number you can calculate from two sets of data that given an indication of if there's a correlation between them, and how tight that correlation is. You can calculate this in Excel simply by using the RSQ(range1, range2) on two ranges of data (like two columns). Here I calculate it for the straight-ticket voters vs. the individual candidate voters. I do this for both Biden and Trump.
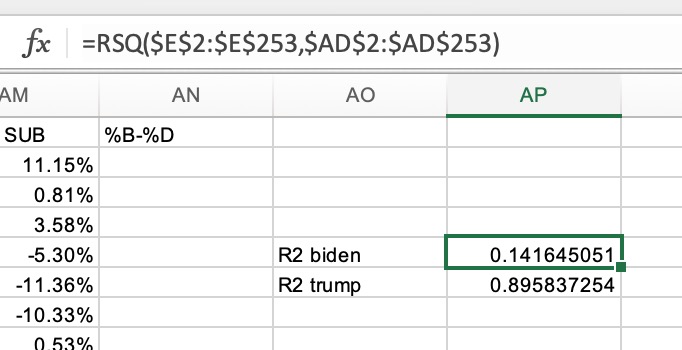
That looks a bit more complicated than it is. $E$2:$E$253 is just specifying column E, rows 2-253
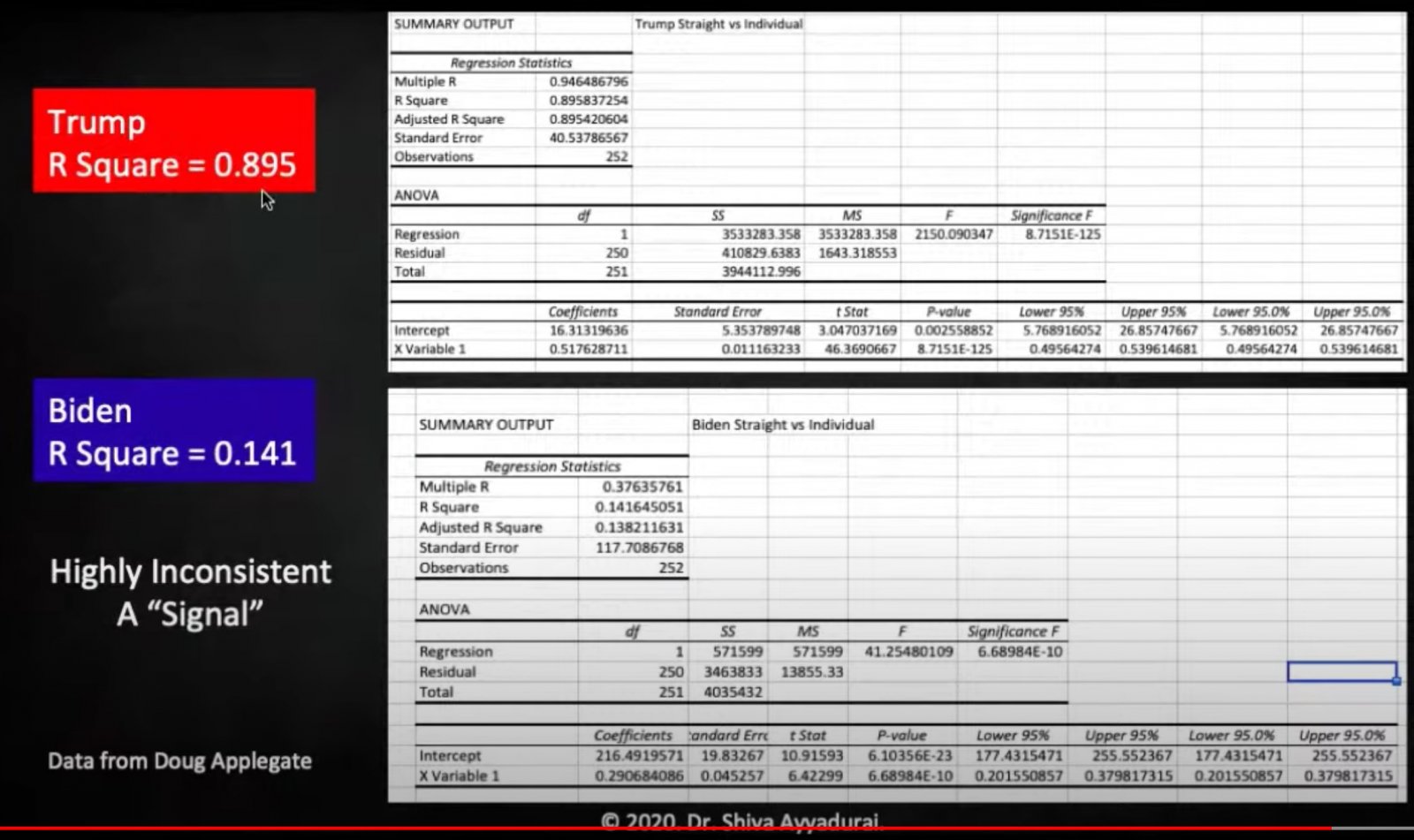
As you can see, Biden's R-Squared (which I'm going to abbreviate as R2) is 0.141, and Trump's is 0.896. Very different numbers (R2 can only go from 0 to 1). This difference has been suggested as evidence, a detectable "signal", that indicates election fraud. For example by Dr. Shiva.
What does this mean? Well if you do a scatter-plot of two ranges of data, with one on the X axis, and the other on the Y-axis, then if there is a high correlation, an R2 of near 1.0, then the plot will cluster around a straight line. With data used here, this means that the number of individual votes a candidate is closely proportional to the number of straight party votes they get.
Here I do a scatter-plot, with trendlines for this with Biden and Trump in Kent County,
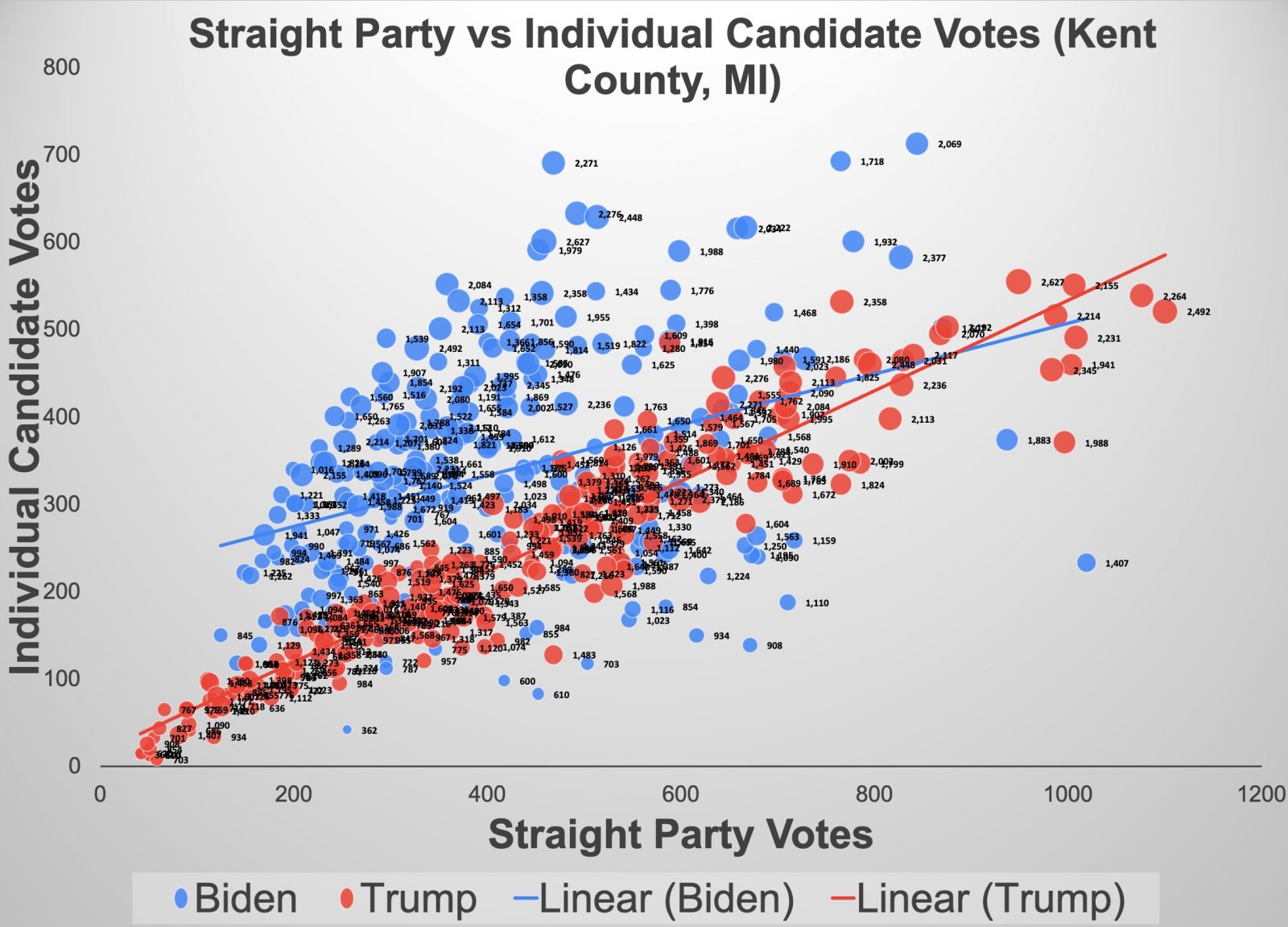
Each dots is one precinct, with the size of the dot (and the number next to it), being the number of votes cast in that precinct. We can see things a bit clearer if we separate out the Tump and Biden graphs.
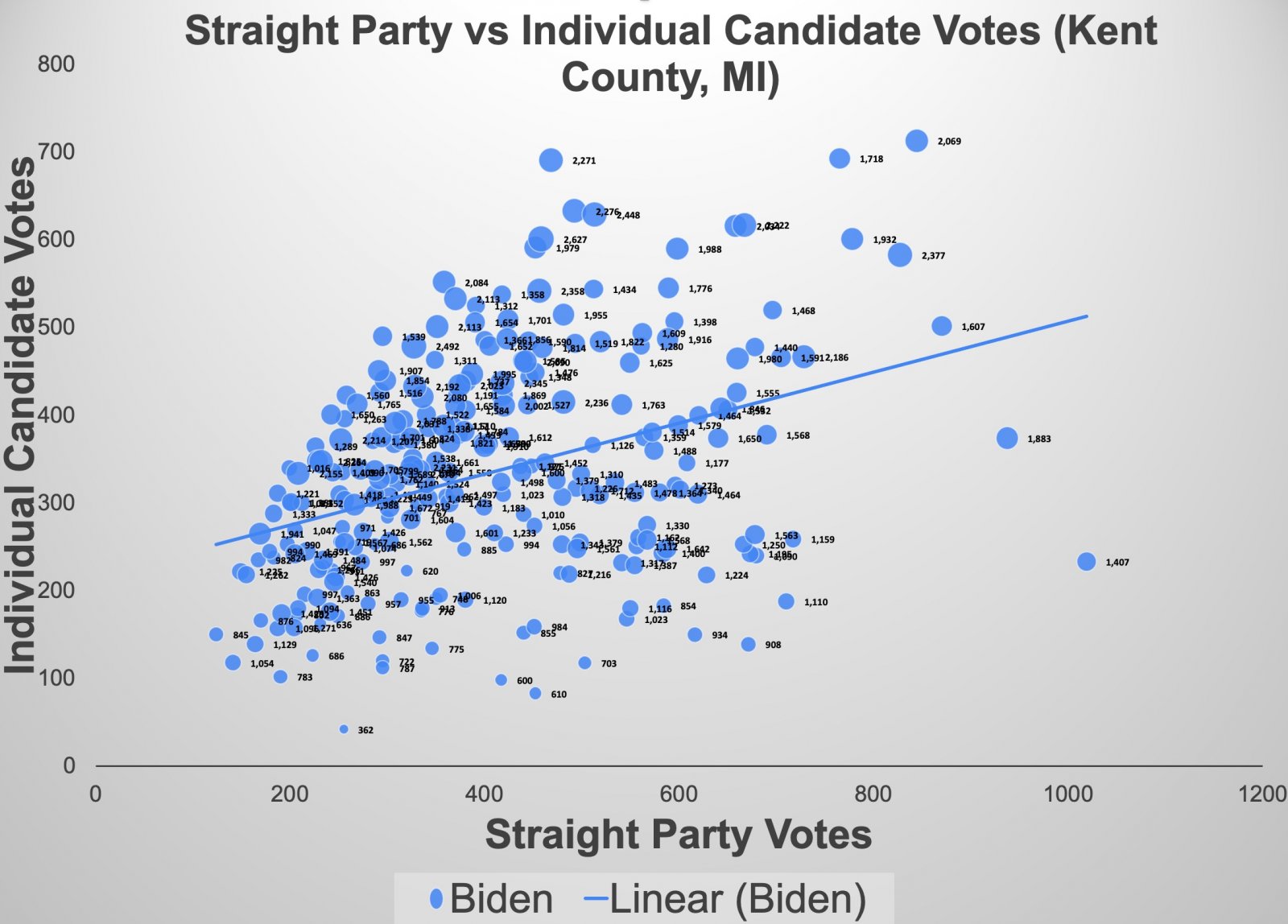
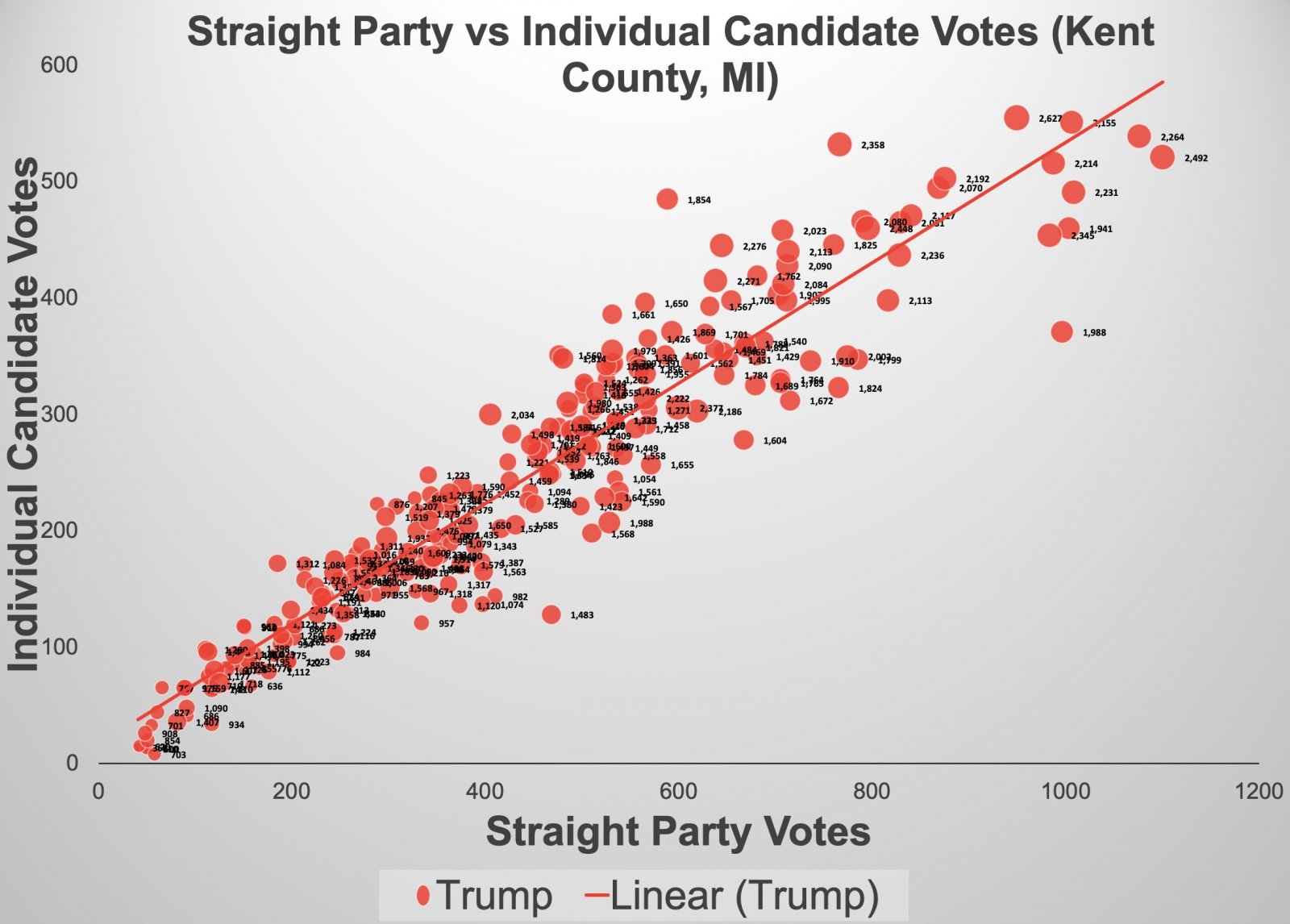
So obvioiusly the pattern, the relationship is different between Trump and Biden. The quesiton is: why? I suspect that there are other variables at play here (probably not fraud), but I'm not sure what they are.
That looks a bit more complicated than it is. $E$2:$E$253 is just specifying column E, rows 2-253
As you can see, Biden's R-Squared (which I'm going to abbreviate as R2) is 0.141, and Trump's is 0.896. Very different numbers (R2 can only go from 0 to 1). This difference has been suggested as evidence, a detectable "signal", that indicates election fraud. For example by Dr. Shiva.
What does this mean? Well if you do a scatter-plot of two ranges of data, with one on the X axis, and the other on the Y-axis, then if there is a high correlation, an R2 of near 1.0, then the plot will cluster around a straight line. With data used here, this means that the number of individual votes a candidate is closely proportional to the number of straight party votes they get.
Here I do a scatter-plot, with trendlines for this with Biden and Trump in Kent County,
Each dots is one precinct, with the size of the dot (and the number next to it), being the number of votes cast in that precinct. We can see things a bit clearer if we separate out the Tump and Biden graphs.
So obvioiusly the pattern, the relationship is different between Trump and Biden. The quesiton is: why? I suspect that there are other variables at play here (probably not fraud), but I'm not sure what they are.
