Travis Taylor (the former chief scientist at the Pentagon's UAP Task Force) made a very specific claim on CBS 8 News Now:
He bases this around a notion of "saturated" that seems poorly defined. Essentially he's using it as a synonym for "overexposed". That means for an individual pixel in an image it's brighter than the maximum value the digital encoding supports, so we can't tell exactly how hot it is relative to other pixels (other it being hotter than all of the unsaturated pixels). There are several problems with the way he uses that, but we can address those later.
The short version of his argument is:
Here are the relevant slides and transcript
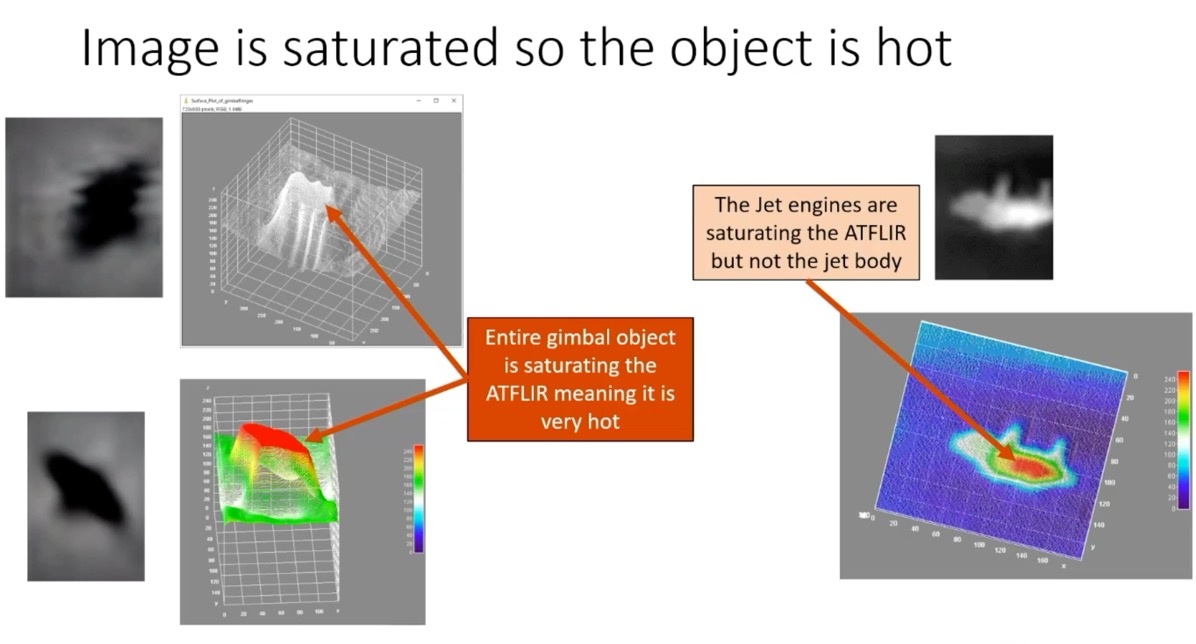

I think this argument fails simply because he's ignoring the effects of exposure settings - or "level" and "gain" on the ATFLIR.
But it might be interesting to replicate his math, see what else there is there.
This comes from work he showed at a recent UFO conference, where he presented an overview of analysis that he claims demonstrates a limit on how far away the Gimbal object can be.From recent calculations I've done, if this device [i.e. Gimbal], whatever this object is, is further away than 8km, then it has to be at the temperature of the melting point of aluminum, and if it's further than 50km, it's at the melting point of steel. That's how hot it would have to be to show up in this way in this sensor. So, it's not a jet that's 50 miles away, and we are getting glare of it
He bases this around a notion of "saturated" that seems poorly defined. Essentially he's using it as a synonym for "overexposed". That means for an individual pixel in an image it's brighter than the maximum value the digital encoding supports, so we can't tell exactly how hot it is relative to other pixels (other it being hotter than all of the unsaturated pixels). There are several problems with the way he uses that, but we can address those later.
The short version of his argument is:
- In another video of a jet, only the region directly around the engine is saturated. (Mick: correct)
- The "entire gimbal object" is saturated, so it is very hot. (Mick: I think we are seeing glare, just from the engine region, obscuring the actual shape)
- With the other video of identifiable jets:
- We can tell the distance to the jet based on trig (Mick: they actually have the distance on-screen and in the audio, so we don't need to, 5.5NM)
- We can use the temperature of jet exhaust and the size of the jet exhaust to calculate how much power is arriving at the ATFLIR for this to be saturation (p_atflir_saturated)
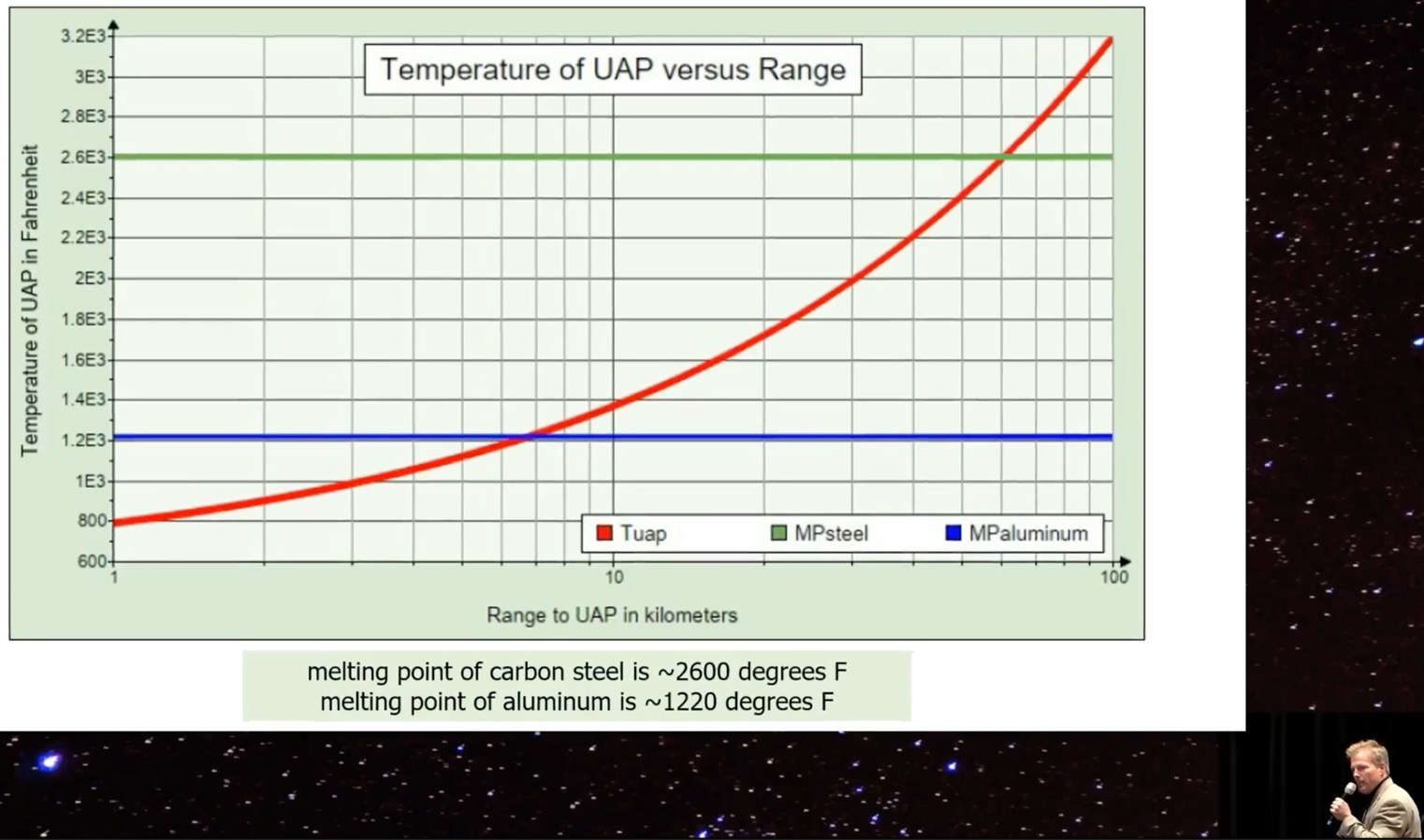
- Given p_atflir_saturated we can calculate how hot the UAP would be at various distances, and make a graph
- The graph shows it must be close, as longer distances require too hot a temperature.
Here are the relevant slides and transcript
So we just want to point out one more thing, that this object is really hot, right. And I want to figure out how hot it is. We now kind of know how big it is, a range. And then we got to figure out how far away it is in the video. See, here's another thing Mick West says it's like 50 miles away. And it's a jet airliner flying and making a certain curve, and they've proven that you can have a jet airliner that gives the motion that's in the video and, and all this kind of stuff. And I looked and I said "really, dude is saturating the camera. A jet airliner gonna saturate the camera at 50 miles away? So I've took the video of the F-18 that we have, we know that it only saturates the camera at the jet engine at the Jet Engine, right?
Well, first thing we need to do is figure out how far away this thing is. So looking at the video, there's information in the video about its magnification of this of the jet of what the magnification of the camera is, we know that the jet is 17.1 meters in one dimension. Now, I can look at the field of view in the camera and say, well, this much is 17 meters. So the whole thing is, says my ruler, right, I can tell you how big the image is in meters. And that tells me how far away it is because I know how far away 17 meters looks like using simple trigonometry. You know, the Pythagoras theorem will tell me all day long, how high that is, if I know this length and that angle, right?
Well, you can look up how hot a jet engine when f 18 gets there, they boast about how great the materials are they've invented that can handle the 1500 degrees Fahrenheit temperature of the combustion engine as it flows out of that thing. And, man, they are so proud of that engine, right? Well, it's pretty cool. Well, so then you can use a thing called the Stefan Boltzmann law.
And you can realize that the heat of this engine is emitting electromagnetic radiation based on this equation on the top right under Stefan Boltzmann law, and it tells you the power that is coming out of the jet in optical power, meaning like, you know, you talked about your lights being 100 Watts, or lumens or whatever. That's exactly what this law tells us is how many watts of power per square meters, well actually is how many watts per power is coming out of the jet engine, when it's saturated at this distance. So I can use that equation and calculate back to my target, knowing the distance now, exactly how much power was on the aperture of my ATFLIR that saturated those pixels. So I know exactly, 1500 degrees at this range saturates the pixels. This tells me this is the threshold of saturation for the FLIR. Well, Raytheon probably didn't want anybody to figure that out, either. So now I can tell you if I know how big an object is, and I know that it's saturating the camera, how far away it is based on this math right here. And so I created this bottom equation is the temperature of the UAP in range, and I did it in kilometers, and I did it in Fahrenheit, so we can speak in Fahrenheit. My math had to use, you know, the Kelvin because that's what the Boltzmann law uses, but so it's converted so that you can understand what you're seeing and so, what we can see from this data alone, just from these videos that I've got that the UAP is somewhere in this range of heat.
And based on distance, so if the far left of the bottom of the screen is one kilometer away, the far right is 100 kilometers away. Well, when it gets to 20, 30, 40, 50, 60, 70 kilometers, if that thing was 70 kilometers away, which is about what, 30 miles or something, if it was that far, no, that's seven kilometers, I'm sorry, seven kilometers. So that's, that's three miles do you three and a half miles, right. So if it's three and a half miles away, it's hot enough to melt aluminum. That's what the blue line is, is the melting point of aluminum. Right now at if you come on out here to 10,20, 30,40,50,60 kilometers away, 60 kilometers away. Now that's about 30 miles or so. All right. It's 60 kilometers away, it's at the melting point of steel. We don't have vehicles that can do that. And they're saying in the video that they the math, they figured out that this was an airliner, you know, 40 miles away, or whatever it was, that means it's in this range somewhere that is so damn hot. That is melted aluminum and or the steel. So guess what? It ain't a damn jet airliner. Right? Right. [applause]
And this is the part that he threw out. He's not going to talk about that part of it. He only wants to talk about well, I know is glare and the gimbal. .... the gimbal jumping into blah, blah, blah, well, whatever the math was good you did you get you tracking it, you know how the gimbal works great. But what you've thrown out is some of the data instead of looking at all the data to figure out the problem. This is a smoking gun, folks. We don't have a drone that can be that hot. Even at you know, seven miles away. It's not flying around being or three miles five miles or whatever it is flying around being as hot as the melting point of aluminum. Those jet engines are only 1500 degrees Fahrenheit. And we're talking about right there. You're already at 1200 degrees Fahrenheit. So what is that? What is this thing and why is it so dadgum hot? So that's that's where I am what with this so far.
I think this argument fails simply because he's ignoring the effects of exposure settings - or "level" and "gain" on the ATFLIR.
But it might be interesting to replicate his math, see what else there is there.
Last edited:
