Priyadi
Member
The antipode of a point on Earth is the point opposite to it. Any flights between the two points should cover approximately the same distance, no matter the direction it travels. These flights cannot be explained by the flat-Earth model and can be used to rule out a flat Earth.
For this purpose, we need two large airports, with the position of one airport as close as possible to the antipodal point of the second airport. To determine these ideal antipodal pairs, I used the data from Top 1000 busiest airports in the world and OpenFlights for the coordinates. First, I merged multiple airports for a single city. Then, for every possible combination, I filtered only the pairs that have more than 5000000 passengers in a year, then sorted them by their antipodal distance. These are the top 20 of the pairs:
Some of the interesting pairs:
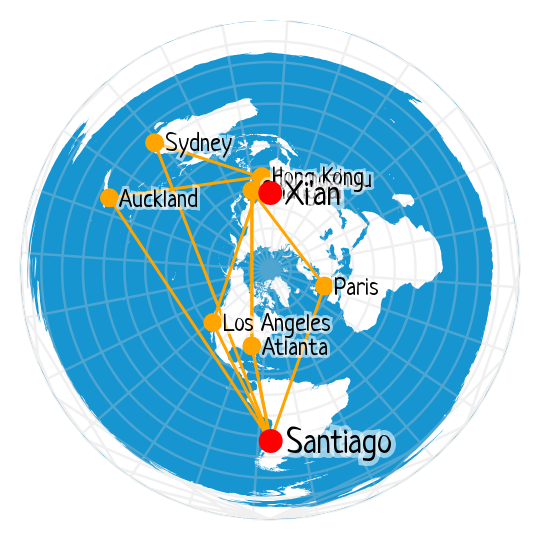
Xi'an – Santiago
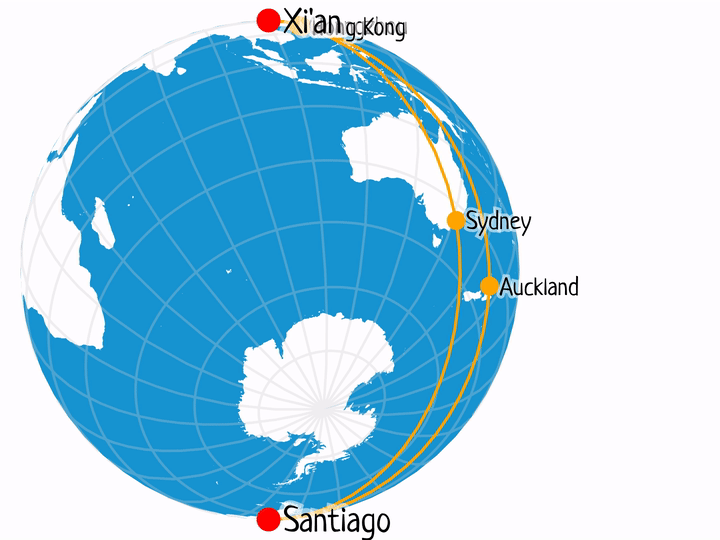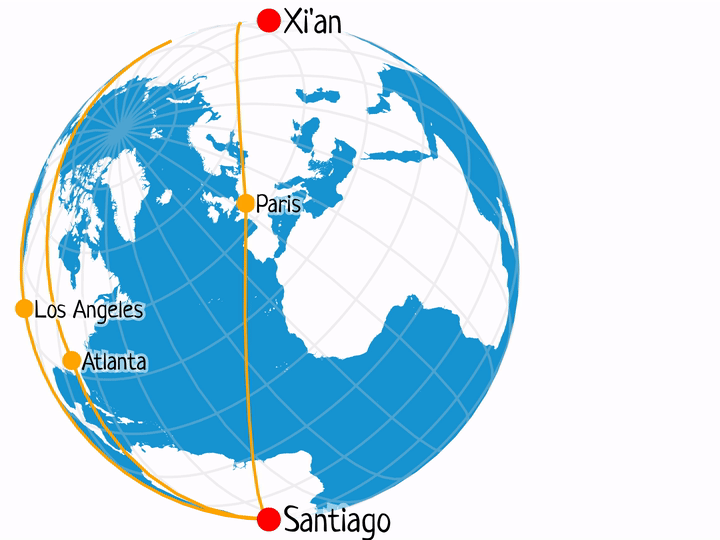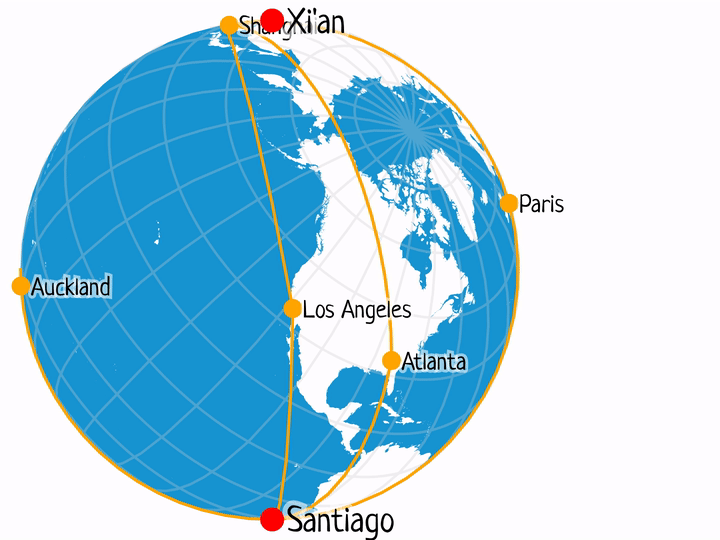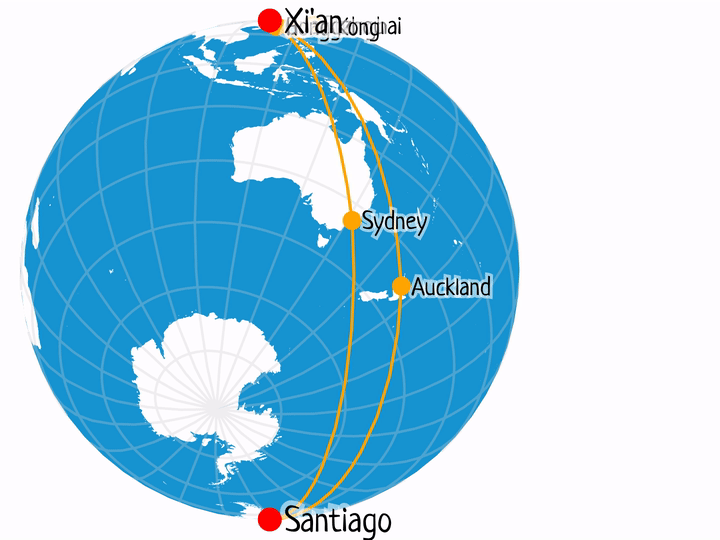
Selected flight durations:
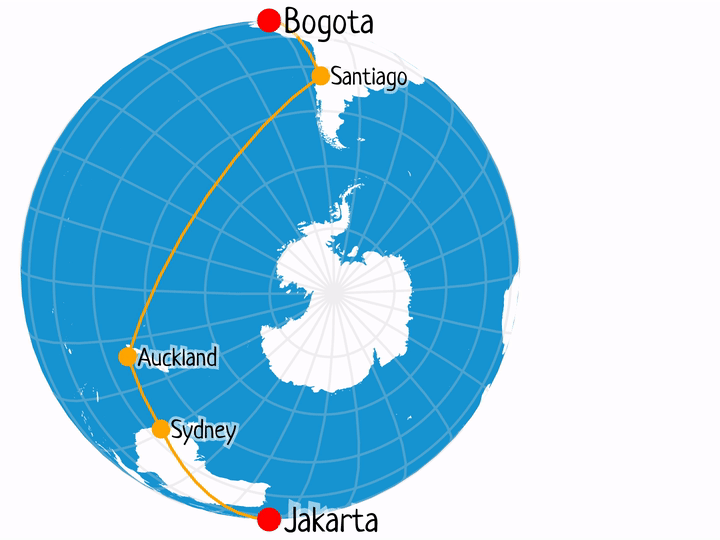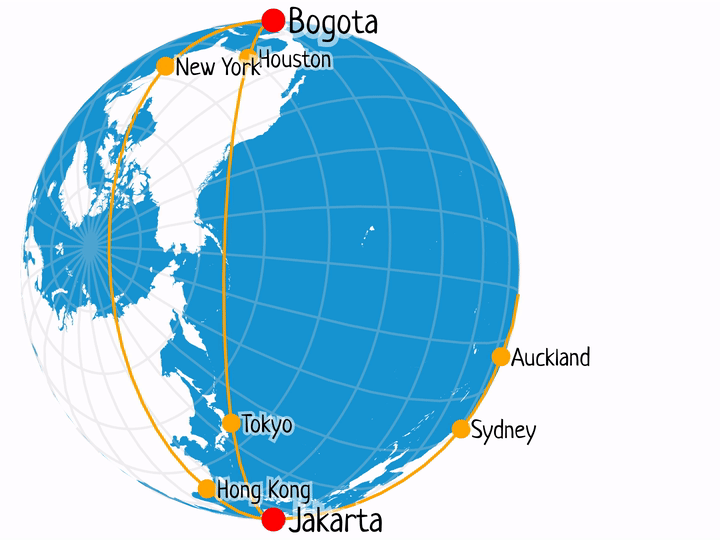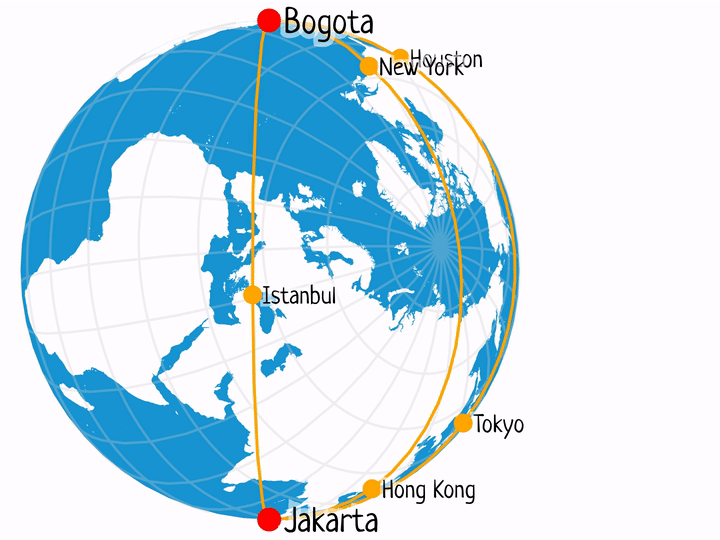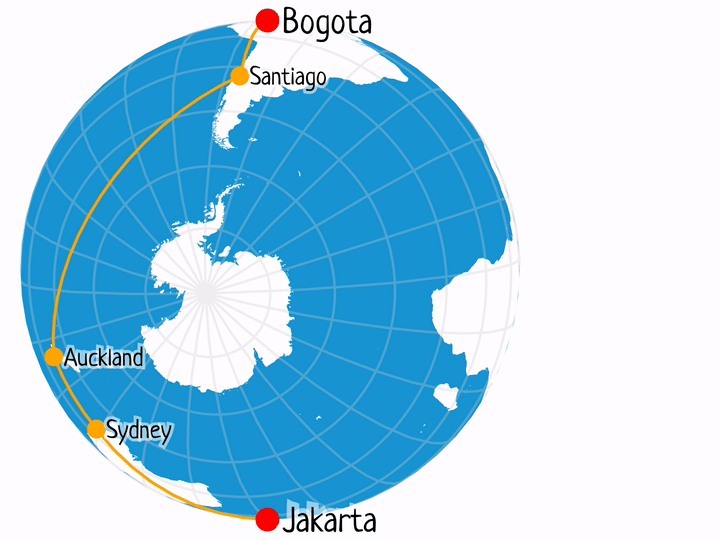
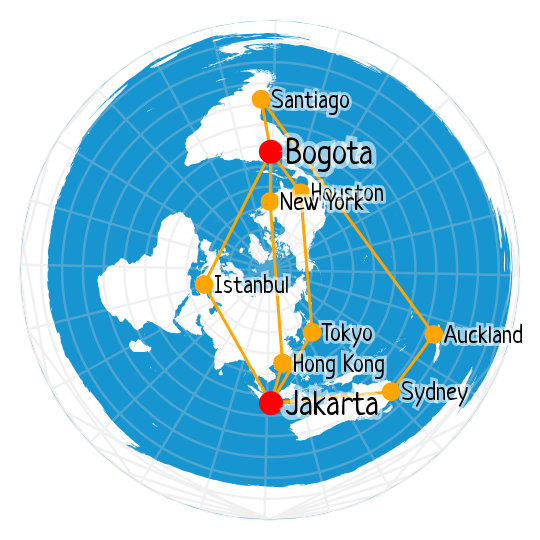
Jakarta – Bogota
Shanghai – Buenos Aires
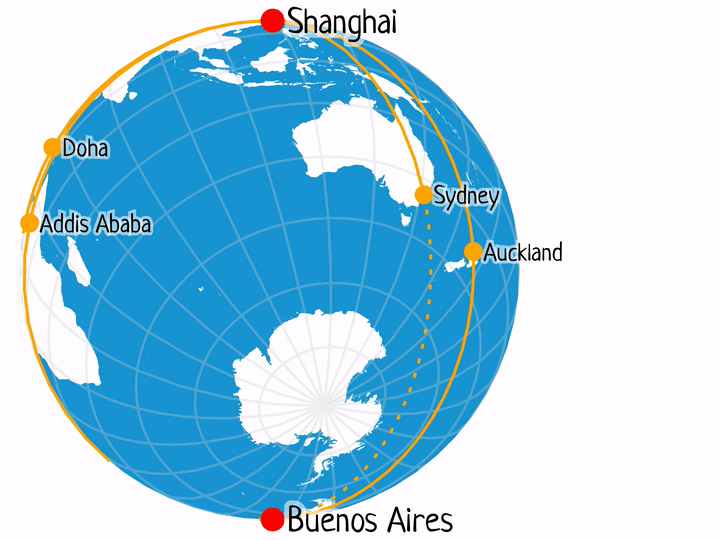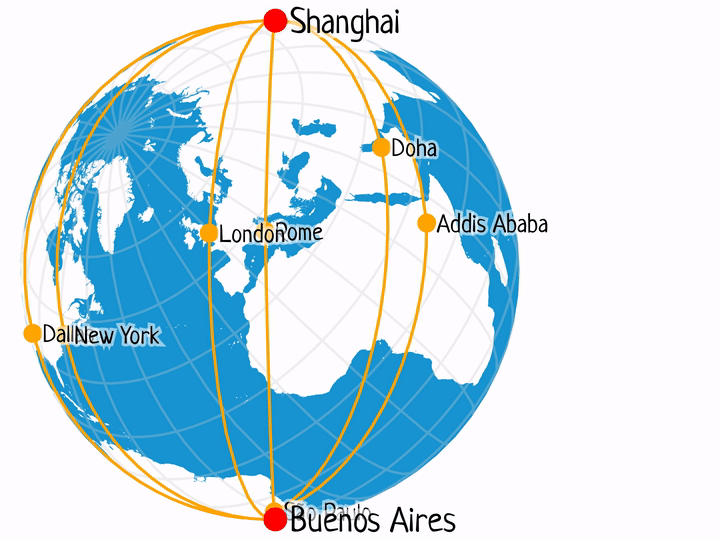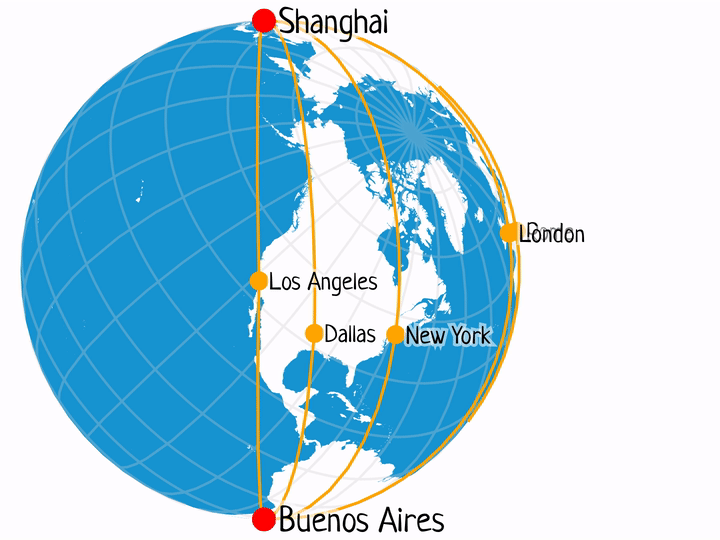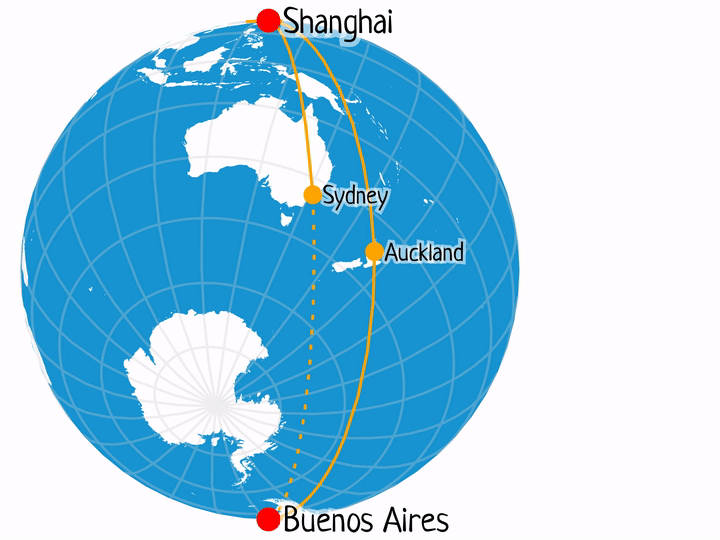
This is possibly the best example from the list, with plenty of one-stop flights between the two locations every day.
For this purpose, we need two large airports, with the position of one airport as close as possible to the antipodal point of the second airport. To determine these ideal antipodal pairs, I used the data from Top 1000 busiest airports in the world and OpenFlights for the coordinates. First, I merged multiple airports for a single city. Then, for every possible combination, I filtered only the pairs that have more than 5000000 passengers in a year, then sorted them by their antipodal distance. These are the top 20 of the pairs:
- Auckland - New Zealand // Malaga - Spain // 18628876 // 0.6579251440332874
- Auckland - New Zealand // Sevilla - Spain // 5108807 // 0.682434752892215
- Xi'an - China // Santiago - Chile // 22316093 // 1.1217059425879221
- Madrid - Spain // Wellington - New Zealand // 6049194 // 1.501238991685529
- Jakarta - Indonesia // Bogota - Colombia // 30989932 // 1.7529934795927706
- Qingdao - China // Buenos Aires - Argentina // 23210530 // 1.832839477995116
- Bogota - Colombia // Palembang - Indonesia // 5677234 // 2.1390957517972455
- Auckland - New Zealand // Faro - Portugal // 8727000 // 2.2021768129792982
- Porto - Portugal // Christchurch - New Zealand // 6566598 // 2.4138603271843246
- Porto Alegre - Brazil // Kagoshima - Japan // 5220710 // 2.4296432539059474
- Porto - Portugal // Wellington - New Zealand // 6049194 // 2.620707352522477
- Buenos Aires - Argentina // Yantai - China // 6503015 // 2.7137816843231928
- Bangkok - Thailand // Lima - Peru // 22046042 // 2.790110528558645
- Okinawa - Japan // Curitiba - Brazil // 6722058 // 2.936611946865315
- Buenos Aires - Argentina // Wuxi - China // 6683380 // 3.3253744953604043
- Shanghai - China // Buenos Aires - Argentina // 24124913 // 3.5200649177134395
- Lisbon - Portugal // Auckland - New Zealand // 19020573 // 3.5705363309106013
- Madrid - Spain // Auckland - New Zealand // 19020573 // 3.6937256985747178
- Nanjing - China // Buenos Aires - Argentina // 24124913 // 3.6950470028545666
- Fukuoka - Japan // Porto Alegre - Brazil // 8012114 // 3.8469693566003396
Some of the interesting pairs:
Xi'an – Santiago
Selected flight durations:
- XIY-PVG-ATL-SCL: 2h 15m + 15h 1m + 9h 29m = 26.75h
- XIY-HKG-AKL-SCL: 3h 10m + 11h 5m + 11h 0m = 25.25h
- XIY-CAN-SYD-SCL: 2h 40m + 9h 25m + 12h 30m = 24.58h
Jakarta – Bogota
- BOG-SCL-AKL-SYD-CGK: 5h 40m + 12h 25m + 3h 35m + 7h 40m = 29.3h
- BOG-JFK-HKG-CGK: 5h 50m + 16h 15m + 4h 45m = 28.83h
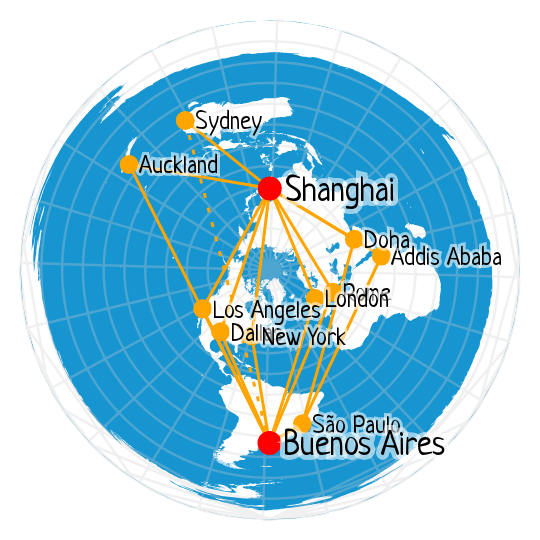
Shanghai – Buenos Aires
This is possibly the best example from the list, with plenty of one-stop flights between the two locations every day.
- PVG-LAX-EZE: 11h 35m + 11h 58m = 23.55 h
- PVG-AKL-EZE: 11h 20m + 11h 45m = 22.78 h
- PVG-ADD-GRU-EZE: 11h 30m + 12h 5m + 3h 15m = 26.83 h
- PVG-JFK-EZE: 14h 55m + 10h 55m = 25.83 h
