Yeah ok. Scale has no bearing in your world mayb. The distance proportionally between the floor in Micks model is what exactly?
I note not ONE PERSON made a estimate when I asked. You included.
.
People didn;t feel it was relevant.
Unlike 1) Richard Gage's Model of cardboard boxes that just has 2 ridiculously strong hollow shells to represent separate parts of the building, Or 2) Cole's Model where he had no core, but very strong single piece outside walls and floor connections that were stronger than the floors themselves or 3) Cole's other models with Pizza thingies that effectively gave each floor many many small vertical columns in between each floor, We instead have 4) Micks;s Model.
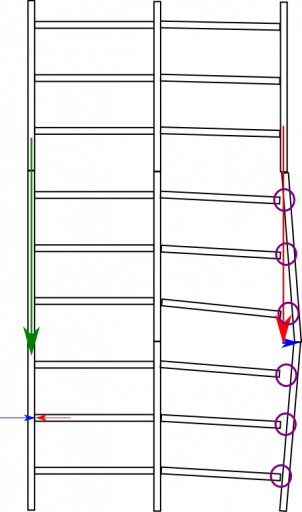
Mick's model possesses a strong inner core made out of sections, where the weakest point is the connectors between sections. He has outer walls, also made in sections where again the weakest point is the connectors between sections. He then has floors which connect the core to the walls.
The core is providing much of the structural strength of the building where the floors themselves hold the core and walls together and give lateral and torsional stability to the core.
The weakest point here is again the connectors that connect the floor to the walls and the columns.
The floors are strong enough for entire building sections to be picked up by the floors.
The whole building is stable and sways a little but doesn't collapse from sideways forces. It can take a force of a relatively large weight being smacked into the side of it.
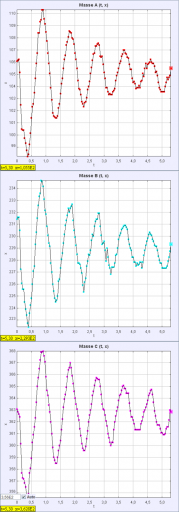
Each floor can hold ( I think it was ) 10 floors of static load. and certainly 6 floors of dynamic load if the load is only dropped from a very small distance.
HOWEVER, if the weight of 2 floors is dropped from the height of one floor, the dynamic load causes the floor to collapse, and all this weight then crashes down by another floors height onto the next floor Which then collapses for the same reason, causing a progressive collapse all the way down the building, unless way more than one floor's worth of material is ejected for each floor travelled.
The walls and core, now having lost the stability the floors were giving them then collapse too, breaking at the connectors also.
It is completely irrelevant how many floors there are in the building, as this mechanism will happen however many there are. Therefore the height to width of the building model is not relevant either.
As far as Mick's model is concerned, one floor is one floor.